Súradnice a vektory. Komplexný sprievodca (2020). Vektory pre atrapy. Akcie s vektormi. Vektorové súradnice. Najjednoduchšie problémy s vektormi Súradnice stredného bodu segmentu vektorového vzorca

V tomto článku začneme diskusiu o jednej „čarovnej paličke“, ktorá vám umožní zredukovať mnohé problémy s geometriou na jednoduchú aritmetiku. Táto „palica“ vám môže výrazne uľahčiť život, najmä v prípade, ak sa cítite neistí pri stavbe priestorových figúr, sekcií atď. To všetko vyžaduje určitú predstavivosť a praktické zručnosti. Metóda, ktorú tu začneme zvažovať, vám umožní takmer úplne sa abstrahovať od všetkých druhov geometrických konštrukcií a uvažovania. Metóda sa nazýva "Súradnicová metóda"... V tomto článku zvážime nasledujúce otázky:

1. Súradnicová rovina
2. Body a vektory v rovine
3. Zostrojenie vektora z dvoch bodov
4. Dĺžka vektora (vzdialenosť medzi dvoma bodmi)
5. Súradnice stredového bodu
6. Bodový súčin vektorov
7. Uhol medzi dvoma vektormi

Myslím, že ste už uhádli, prečo sa tak nazýva súradnicová metóda? Je pravda, že dostal také meno, pretože nepracuje s geometrickými objektmi, ale s ich číselnými charakteristikami (súradnice). A samotná transformácia, ktorá umožňuje prejsť z geometrie na algebru, spočíva v zavedení súradnicového systému. Ak bol pôvodný obrázok plochý, súradnice sú dvojrozmerné a ak je obrázok trojrozmerné, súradnice sú trojrozmerné. V tomto článku sa budeme zaoberať iba dvojrozmerným prípadom. A hlavným cieľom článku je naučiť vás používať niektoré základné techniky súradnicovej metódy (niekedy sa ukážu byť užitočné pri riešení úloh z planimetrie v časti B skúšky). Nasledujúce dve časti na túto tému sú venované diskusii o metódach riešenia úloh C2 (problém stereometrie).

Kde by bolo logické začať diskutovať o súradnicovej metóde? Pravdepodobne z konceptu súradnicového systému. Pamätajte si, keď ste sa s ňou prvýkrát stretli. Zdá sa mi, že v 7. ročníku, keď ste sa dozvedeli napríklad o existencii lineárnej funkcie. Pripomeniem, že ste to postavili bod po bode. Pamätáš si? Vybrali ste ľubovoľné číslo, dosadili ste ho do vzorca a takto ste vypočítali. Napríklad, ak, potom, ak, potom atď. Čo ste nakoniec dostali? A dostali ste body so súradnicami: a. Potom ste nakreslili „krížik“ (súradnicový systém), vybrali na ňom mierku (koľko buniek budete mať ako jednotkový segment) a označíte naň body, ktoré ste získali, ktoré ste potom spojili priamkou, výslednou čiarou je graf funkcie.

Existuje niekoľko bodov, ktoré by vám mali byť vysvetlené trochu podrobnejšie:

1. Z dôvodu pohodlia si vyberiete jeden segment, aby všetko na obrázku pekne a kompaktne zapadlo.

2. Predpokladá sa, že os prechádza zľava doprava a os prechádza zdola nahor.

3. Križujú sa v pravom uhle a bod ich priesečníka sa nazýva pôvod. Je to označené písmenom.

4. Napísať súradnice bodu, napríklad vľavo v zátvorkách, súradnice bodu pozdĺž osi a vpravo pozdĺž osi. Najmä to v danej chvíli jednoducho znamená

5. Aby ste mohli nastaviť ľubovoľný bod na súradnicovej osi, musíte zadať jeho súradnice (2 čísla)

6. Pre ľubovoľný bod osi

7. Pre ľubovoľný bod osi

8. Os sa nazýva os x.

9. Os sa nazýva os y.

Teraz urobíme ďalší krok s vami: označte dva body. Spojme tieto dva body so segmentom. A vložíme šípku, ako keby sme kreslili segment z bodu do bodu: to znamená, že urobíme náš segment nasmerovaný!

Pamätajte si, ako sa ešte nazýva smerová čiara? Správne, hovorí sa tomu vektor!

Ak teda spojíme bod s bodom, navyše, začiatok bude bod A a koniec bude bod B, potom dostaneme vektor. Túto formáciu ste robili aj v 8. ročníku, pamätáte si?

Ukazuje sa, že vektory, podobne ako body, môžu byť označené dvoma číslami: tieto čísla sa nazývajú súradnice vektora. Otázka znie: myslíte si, že nám stačí poznať súradnice začiatku a konca vektora, aby sme našli jeho súradnice? Ukazuje sa, že áno! A to sa robí veľmi jednoducho:

Pretože bod vo vektore je začiatok a a je koniec, vektor má nasledujúce súradnice:

Napríklad ak, potom súradnice vektora

Teraz urobíme opak, nájdeme súradnice vektora. Čo na to potrebujeme zmeniť? Áno, musíte vymeniť začiatok a koniec: teraz bude začiatok vektora v bode a koniec bude v bode. Potom:

Pozrite sa pozorne, ako sú vektory a? Ich jediným rozdielom sú značky v súradniciach. Sú protikladní. Je obvyklé napísať túto skutočnosť takto:

Niekedy, ak nie je konkrétne určené, ktorý bod je začiatkom vektora a ktorý je koncom, potom vektory nie sú označené dvoma veľkými písmenami, a jedno malé písmeno, napríklad :, atď.

Teraz trochu prax vyhľadajte súradnice nasledujúcich vektorov:

Vyšetrenie:

Teraz vyriešte problém trochu ťažšie:

Vektor s na-cha-lom v bode má co-or-di-na-ty. Nie všetky body abs-cis-su.

To isté je dosť prozaické: Nech sú súradnice bodu. Potom

Systém som zostavil podľa definície súradníc vektora. Potom má bod súradnice. Máme záujem na osi x. Potom

Odpoveď:

Čo ešte môžete robiť s vektormi? Áno, takmer všetko je rovnaké ako pri bežných číslach (okrem toho, že nemôžete deliť, ale môžete násobiť dvoma spôsobmi, z ktorých jeden tu budeme diskutovať o niečo neskôr)

1. Vektory je možné navzájom dopĺňať
2. Vektory je možné od seba odčítať
3. Vektory môžu byť vynásobené (alebo delené) ľubovoľným nenulovým číslom
4. Vektory sa môžu navzájom znásobovať

Všetky tieto operácie majú veľmi jasné geometrické znázornenie. Napríklad pravidlo pre trojuholník (alebo rovnobežník) pre sčítanie a odčítanie:

Vektor sa rozširuje alebo zmenšuje alebo mení smer, ak je vynásobený alebo delený číslom:

Tu nás však bude zaujímať otázka, čo sa deje so súradnicami.

1. Pri sčítaní (odčítaní) dvoch vektorov sčítame (odčítame) ich súradnice prvok po prvku. Tj.

2. Pri vynásobení (delení) vektora číslom sa všetky jeho súradnice vynásobia (delia) týmto číslom:

Napríklad:

· Nay-di-te súčet ko-or-di-nat vek-to-ra.

Najprv nájdeme súradnice každého z vektorov. Oba majú rovnaký pôvod - bod pôvodu. Ich konce sú rôzne. Potom,. Teraz vypočítajme súradnice vektora Potom je súčet súradníc výsledného vektora.

Odpoveď:

Teraz vyriešte nasledujúci problém sami:

Nájdite súčet súradníc vektora

Kontrolujeme:

Uvažujme teraz o nasledujúcom probléme: máme na mysli dva body súradnicová rovina... Ako zistiť vzdialenosť medzi nimi? Nechajte prvý bod byť a druhý. Označme vzdialenosť medzi nimi. Pre prehľadnosť urobme nasledujúci výkres:

Čo som urobil? Najprv som sa spojil body a, a tiež z bodu som nakreslil čiaru rovnobežnú s osou a z bodu som nakreslil čiaru rovnobežnú s osou. Pretnuli sa v bode a vytvorili tak nádhernú postavu? Čím je pozoruhodný? Áno, ty a ja vieme takmer všetko správny trojuholník... No, Pytagorova veta - to určite. Hľadaný segment je preponou tohto trojuholníka a segmentmi sú nohy. Aké sú súradnice bodu? Áno, je ich ľahké nájsť na obrázku: Pretože segmenty sú rovnobežné s osami a podľa toho sa dajú ľahko nájsť ich dĺžky: ak označíte dĺžky segmentov podľa, potom

Teraz použijeme Pytagorovu vetu. Poznáme dĺžky nôh, nájdeme preponu:

Vzdialenosť medzi dvoma bodmi je teda koreňom súčtu druhých mocnín rozdielov zo súradníc. Alebo - vzdialenosť medzi dvoma bodmi je dĺžka čiary, ktorá ich spája. Je ľahké vidieť, že vzdialenosť medzi bodmi je nezávislá na smere. Potom:

Z toho vyvodzujeme tri závery:

Poďme si trochu precvičiť výpočet vzdialenosti medzi dvoma bodmi:

Napríklad, ak, potom je vzdialenosť medzi a rovná

Alebo poďme inak: nájdite súradnice vektora

A nájdite dĺžku vektora:

Ako vidíte, to isté!

Teraz si zacvičte sami:

Úloha: nájdite vzdialenosť medzi zadanými bodmi:

Kontrolujeme:

Tu je niekoľko ďalších problémov s rovnakým vzorcom, aj keď znejú trochu inak:

1. Štvorec Nay-di-te s dĺžkou od storočia do ra.

2. Nay-di-te square-rat o dĺžke storočia do ra

Myslím, že ste sa s nimi ľahko vysporiadali? Kontrolujeme:

1. A to je pre pozornosť) Súradnice vektorov sme už našli a skôr :. Potom má vektor súradnice. Štvorec jeho dĺžky sa bude rovnať:

2. Nájdite súradnice vektora

Potom je štvorec jeho dĺžky

Nič zložité, však? Jednoduchá aritmetika, nič viac.

Nasledujúce úlohy nemožno kategorizovať jednoznačne, je väčšia pravdepodobnosť, že budú mať všeobecnú erudíciu a schopnosť kresliť jednoduché obrázky.

1. Nay-di-te sínus uhla s prerušením, co-uni-nya-yu-shch-tého bodu s osou osi x.

a

Čo tu budeme robiť? Musíte nájsť sínus uhla medzi a osou. A kde vieme, ako hľadať sínus? Je to tak, v pravouhlom trojuholníku. Čo teda musíme urobiť? Postavte tento trojuholník!

Pretože súradnice bodu sú a, segment je rovnaký a segment. Musíme nájsť sínus uhla. Pripomeniem, že sínus je teda pomer opačnej nohy k prepone

Čo nám zostáva urobiť? Nájdite preponu. Môžete to urobiť dvoma spôsobmi: pomocou Pytagorovej vety (nohy sú známe!) Alebo podľa vzorca pre vzdialenosť medzi dvoma bodmi (v skutočnosti to isté ako pri prvom spôsobe!). Pôjdem druhým spôsobom:

Odpoveď:

Ďalšia úloha sa vám bude zdať ešte jednoduchšia. Ona - na súradniciach bodu.

Cieľ 2. Per-pen-di-ku-lar je spustené z bodu na os abs-ciss. Nay-di-te abs-cis-su os-no-va-nia per-pen-di-ku-la-ra.

Urobme si kresbu:

Základom kolmice je bod, v ktorom pretína os (osi) osi x, pre mňa je to bod. Obrázok ukazuje, že má súradnice :. Máme záujem na osi x - teda na zložke „x“. Je to rovnocenné

Odpoveď: .

Cieľ 3. Za podmienok predchádzajúceho problému nájdite súčet vzdialeností od bodu k súradnicovým osiam.

Úloha je spravidla elementárna, ak viete, aká je vzdialenosť medzi bodom a osami. Vieš? Dúfam, ale stále vám pripomínam:

Takže na svojom obrázku, umiestnenom o niečo vyššie, som už nakreslil jednu takú kolmú? Na ktorú os to má byť? Na os. A aká je potom jeho dĺžka? Je to rovnocenné Teraz nakreslite kolmicu na os sami a nájdite jej dĺžku. Bude to rovnaké, nie? Potom je ich súčet rovnaký.

Odpoveď: .

Úloha 4. V podmienkach úlohy 2 nájdite súradnicu bodu symetrickú k bodu relatívne k osi x.

Myslím, že intuitívne rozumiete, čo je symetria? Mnoho objektov to má: veľa budov, stolov, lietadiel, mnoho geometrických tvarov: guľa, valec, štvorec, kosoštvorec, atď. Symetriu možno zhruba chápať takto: figúrka sa skladá z dvoch (alebo viacerých) rovnakých polovíc. Táto symetria sa nazýva axiálna. Čo je potom os? To je presne čiara, pozdĺž ktorej môže byť postava relatívne povedané „rozrezaná“ na identické polovice (na tomto obrázku je os symetrie priamka):

Teraz sa vráťme k nášmu problému. Vieme, že hľadáme bod, ktorý je symetrický k osi. Potom je táto os osou symetrie. To znamená, že musíme označiť bod tak, aby os rozdelila segment na dve rovnaké časti. Skúste taký bod označiť sami. Teraz porovnajte s mojím riešením:

Urobili ste to isté? Dobre! V nájdenom bode nás zaujíma súradnica. Je si rovna

Odpoveď:

Teraz mi povedzte, po premýšľaní o sekundách, aká bude osa bodu symetrického k bodu A vzhľadom na súradnicu? Aká je tvoja odpoveď? Správna odpoveď: .

Vo všeobecnosti možno pravidlo napísať takto:

Bod symetrický k bodu vzhľadom na os x má súradnice:

Bod symetrický k bodu okolo osi súradnice má súradnice:

No teraz je to úplne desivé úloha: nájdite súradnice bodu symetrické k bodu vzhľadom na pôvod. Najprv sa nad sebou zamyslite a potom sa pozrite na moju kresbu!

Odpoveď:

Teraz problém rovnobežníka:

Úloha 5: Body sú ver-shi-na-mi paral-le-lo-gram-ma. Body Nay-di-te alebo-di-na-tu.

Tento problém môžete vyriešiť dvoma spôsobmi: logikou a metódou súradníc. Najprv použijem súradnicovú metódu a potom vám poviem, ako ju môžete vyriešiť inak.

Je úplne zrejmé, že os x bodu je rovná. (leží na kolmici nakreslenej z bodu na os x). Musíme nájsť súradnicu. Využime to, že naša postava je rovnobežník, to znamená, že. Nájdite dĺžku segmentu pomocou vzorca pre vzdialenosť medzi dvoma bodmi:

Spustíme kolmicu spájajúcu bod s osou. Križovatkový bod bude označený písmenom.

Dĺžka segmentu je. (nájdite samotný problém, kde sme diskutovali o tomto bode), potom nájdeme dĺžku segmentu podľa Pytagorovej vety:

Dĺžka čiary je úplne rovnaká ako jej súradnica.

Odpoveď: .

Iné riešenie (uvediem iba obrázok, ktorý ho ilustruje)

Priebeh riešenia:

1. Správanie

2. Nájdite súradnice bodu a dĺžku

3. Dokáž to.

Ďalší segmentová skladačka:

Body sa objavujú-la-are-Xia ver-shi-na-mi tre-uhlie-ni-ka. Nay-di-te je dĺžka jeho strednej čiary, rovnobežník-lel-noy.

Pamätáte si, čo je stredná čiara trojuholníka? Potom je táto úloha pre vás elementárna. Ak si nepamätáte, potom vám pripomeniem: stredná čiara trojuholníka je čiara, ktorá spája stredy protiľahlých strán. Je rovnobežná so základňou a rovná sa jej polovici.

Základom je úsečka. Jeho dĺžku sme museli hľadať skôr, je rovnaká. Potom je dĺžka strednej čiary polovičná a rovnaká.

Odpoveď: .

Komentár: Tento problém je možné vyriešiť iným spôsobom, na ktorý sa obrátime o niečo neskôr.

Medzitým - je tu pre vás niekoľko úloh, precvičte si ich, sú celkom jednoduché, ale pomôžu vám „dostať sa do ruky“ pomocou metódy súradníc!

1. Body sú ver-shi-na-mi tra-pettii. Nay-di-te je dĺžka jeho strednej čiary.

2. Bodky a are-la-sy-ver-shi-na-mi pa-ra-le-lo-gram-ma. Body Nay-di-te alebo-di-na-tu.

3. Nay-di-te dĺžka odrezaného, ​​co-uni-nya-yu-shch-go bodu a

4. Nay-di-te oblasť krásnych fi-gu-ry v rovine co-or-di-nat-noy.

5. Kruh so stredom na-cha-le ko-or-di-nat prechádza bodom. Nay-di-te jej ra-di-us.

6. Nai-di-te ra-di-us kruhu, popísané-san-noy v blízkosti obdĺžnikového-nik-ka, vrcholy ko-to-ro-go majú co-op -di-na-you spoluveter-ale

Riešenie:

1. Je známe, že stredná čiara lichobežníka sa rovná polovičnému súčtu jeho základov. Základňa je rovnaká a základňa je. Potom

Odpoveď:

2. Najľahší spôsob, ako vyriešiť tento problém, je všimnúť si to (pravidlo rovnobežníka). Vypočítajte súradnice vektorov a nie je to ťažké :. Keď sa pridajú vektory, pridajú sa súradnice. Potom má súradnice. Bod má tiež rovnaké súradnice, pretože pôvod vektora je bod so súradnicami. Máme záujem o súradnicu. Je to rovnocenné

Odpoveď:

3. Konáme okamžite podľa vzorca pre vzdialenosť medzi dvoma bodmi:

Odpoveď:

4. Pozrite sa na obrázok a povedzte mi, medzi ktorými dvoma tvarmi je tieňovaná oblasť „obložená“? Je vložený medzi dve námestia. Potom sa plocha požadovaného obrázku rovná ploche veľkého štvorca mínus plocha malého. Strana malého štvorca je úsečka spájajúca body a jeho dĺžka je

Potom je plocha malého štvorca

To isté robíme s veľkým štvorcom: jeho strana je segment spájajúci body a jeho dĺžka je

Potom je plocha veľkého námestia

Plochu požadovaného obrázku nájdeme podľa vzorca:

Odpoveď:

5. Ak má kruh ako stred počiatok súradníc a prechádza bodom, jeho polomer sa bude presne rovnať dĺžke segmentu (nakreslite obrázok a pochopíte, prečo je to zrejmé). Nájdeme dĺžku tohto segmentu:

Odpoveď:

6. Je známe, že polomer kruhu ohraničeného obdĺžnikom sa rovná polovici jeho uhlopriečky. Nájdeme dĺžku ktorejkoľvek z dvoch uhlopriečok (koniec koncov, v obdĺžniku sú rovnaké!)

Odpoveď:

No už ste sa so všetkým vyrovnali? Nebolo to veľmi ťažké prísť na to, však? Platí tu jedno - vedieť si urobiť vizuálny obraz a jednoducho z neho „prečítať“ všetky údaje.

Zostáva nám veľmi málo. Doslova existujú ďalšie dva body, o ktorých by som chcel diskutovať.

Pokúsme sa vyriešiť tento jednoduchý problém. Nech sú dva body a budú dané. Nájdite súradnice stredného bodu segmentu. Riešenie tohto problému je nasledovné: nech je bod požadovaným stredom, potom má súradnice:

Tj. súradnice stredného bodu = aritmetický priemer zodpovedajúcich súradníc koncov segmentov.

Toto pravidlo je veľmi jednoduché a zvyčajne študentom nespôsobuje ťažkosti. Pozrime sa, aké úlohy a ako sa používajú:

1. Bod Nay-di-te or-di-na-tu-re-di-us from-cut, co-uni-nya-yu-shch-go a

2. Body sú-la-yut-sya ver-shi-na-mi-you-rekh-uhlie-no-ka. Nay-di-te or-di-na-tu body pe-re-se-ch-niya his dia-go-na-lei.

3. Nie-di-tie abs-cis-su stred-tra kruhu, popísané-san-noy v blízkosti uhlia-no-ka, vrcholy ko-to-ro-go majú co-op-di- na-ty co-vet-ale.

Riešenie:

1. Prvý problém je len klasický. Konáme okamžite, aby sme určili stred segmentu. Má súradnice. Ordinácia je.

Odpoveď:

2. Je ľahké vidieť, že daný štvoruholník je rovnobežník (dokonca aj kosoštvorec!). Sami to môžete dokázať vypočítaním dĺžok strán a ich vzájomným porovnaním. Čo viem o rovnobežníku? Jeho uhlopriečky sú polovicou priesečníka! Aha! Čo je teda priesečníkom uhlopriečok? Toto je stred akejkoľvek uhlopriečky! Vyberiem si najmä uhlopriečku. Potom má bod súradnice Súradnica bodu je rovná.

Odpoveď:

3. Čím je stred kruhu ohraničený obdĺžnikom? Zhoduje sa s priesečníkom jeho uhlopriečok. Čo viete o uhlopriečkach obdĺžnika? Sú rovnaké a bod priesečníka je polovičný. Úloha bola zredukovaná na predchádzajúcu. Vezmite si napríklad uhlopriečku. Potom, ak je stred ohraničeného kruhu, potom je stred. Hľadanie súradníc: Abscissa je rovnaká.

Odpoveď:

Teraz si trochu zacvičte, na každý problém uvediem len odpovede, aby ste sa mohli otestovať.

1. Nai-di-te ra-di-us kruhu, popísané-san-noy okolo trojuholníka, vrcholy co-to-ro-go majú hmly co-or-di -no

2. Nai-di-te alebo-di-na-tu stredová dráha kruhu, opis-san-noy okolo trojuholníka-nik, vrcholy ko-to-ro-go majú súradnice

3. Ako na ra-di-u-sa má byť v bode kruh so stredom tak, aby bol na osi abs-cissa?

4. Body Nay-di-te alebo-di-na-tu bodu pe-re-se-ch-nia osi a odrezaný, co-uni-nya-yu-shch-go bod a

Odpovede:

Uspeli ste? Naozaj v to dúfam! Teraz - posledné stlačenie. Teraz buďte obzvlášť opatrní. Materiál, ktorý teraz vysvetlím, priamo súvisí nielen s jednoduché úlohy o metóde súradníc z časti B, ale nachádza sa tiež všade v probléme C2.

Ktoré zo svojich sľubov som ešte nedodržal? Pamätáte si, aké operácie s vektormi som sľúbil zaviesť a aké som nakoniec zaviedol? Som si istý, že som na nič nezabudol? Zabudol! Zabudli ste vysvetliť, čo znamená násobenie vektorov.

Existujú dva spôsoby znásobenia vektora vektorom. V závislosti od zvolenej metódy získame objekty inej povahy:

Krížový produkt je dosť zložitý. Ako to urobiť a na čo to slúži, s vami prediskutujeme v nasledujúcom článku. A v tomto sa zameriame na bodový produkt.

Môžeme to vypočítať dvoma spôsobmi:

Ako ste uhádli, výsledok by mal byť rovnaký! Pozrime sa teda najskôr na prvý spôsob:

Bodový výrobok z hľadiska súradníc

Nájdite: - spoločný bodkový zápis výrobku

Vzorec na výpočet je nasledujúci:

To znamená, že bodový súčin = súčet súčinov súradníc vektorov!

Príklad:

Nai di te

Riešenie:

Nájdeme súradnice každého z vektorov:

Bodový produkt vypočítame podľa vzorca:

Odpoveď:

Vidíte, absolútne nič zložité!

Teraz to vyskúšajte sami:

Nay-di-te scalar-noe pro-iz-ve-de-vek-to-priekopa

Zvládli ste to? Možno ste si všimli malý háčik? Skontrolujme to:

Súradnice vektorov sú rovnaké ako v predchádzajúcej úlohe! Odpoveď:.

Okrem súradnice existuje ešte jeden spôsob výpočtu bodového súčinu, a to pomocou dĺžok vektorov a kosínusu uhla medzi nimi:

Udáva uhol medzi vektormi a.

To znamená, že bodový súčin sa rovná súčinu dĺžok vektorov a kosínusu uhla medzi nimi.

Načo je nám tento druhý vzorec, keď máme prvý, ktorý je oveľa jednoduchší, aspoň v ňom nie sú žiadne kosíny. A je to potrebné, aby sme z prvého a druhého vzorca mohli odvodiť, ako nájsť uhol medzi vektormi!

Potom si zapamätajme vzorec pre dĺžku vektora!

Potom, keď nahradím tieto údaje do vzorca bodového produktu, dostanem:

Ale na druhej strane:

Čo sme teda vy a ja dostali? Teraz máme vzorec na výpočet uhla medzi dvoma vektormi! Niekedy je to pre stručnosť napísané aj takto:

To znamená, že algoritmus na výpočet uhla medzi vektormi je nasledujúci:

1. Vypočítajte bodový súčin z hľadiska súradníc
2. Nájdite dĺžky vektorov a vynásobte ich
3. Výsledok bodu 1 vydelíte výsledkom bodu 2

Poďme si zacvičiť na príkladoch:

1. Nay-di-te je uhol medzi storočím a ra-mi a. Odpovedzte v gra-du-sakh.

2. Za podmienok predchádzajúceho problému nájdite medzi vektormi kosínus

Poďme na to: Pomôžem vám vyriešiť prvý problém a druhý sa pokúsite urobiť sami! Súhlasím? Potom začnime!

1. Tieto vektory sú naši starí známi. Ich bodový súčin sme už spočítali a bol rovnaký. Ich súradnice sú:,. Potom nájdeme ich dĺžky:

Potom hľadáme kosínus medzi vektormi:

Aký je kosínus uhla? Toto je roh.

Odpoveď:

Teraz vyriešte druhý problém sami a potom porovnáme! Dám vám iba veľmi krátke riešenie:

2. má súradnice, má súradnice.

Nech je uhol medzi vektormi a, potom

Odpoveď:

Treba poznamenať, že problémy priamo na vektoroch a spôsob súradníc v časti B skúšobnej práce sú dosť zriedkavé. Drvivú väčšinu problémov s C2 je však možné ľahko vyriešiť zavedením súradnicového systému. Tento článok teda môžete považovať za základ, na základe ktorého urobíme celkom prefíkané stavby, ktoré budeme potrebovať na riešenie zložitých problémov.

KOORDINÁTY A VEKTORY. MEDIUM ROVEN

Ty a ja pokračujeme v štúdiu metódy súradníc. V poslednej časti sme odvodili niekoľko dôležitých vzorcov, ktoré umožňujú:

1. Nájdite vektorové súradnice
2. Nájdite dĺžku vektora (alternatívne: vzdialenosť medzi dvoma bodmi)
3. Sčítajte, odčítajte vektory. Vynásobte ich skutočným číslom
4. Nájdite stred úsečky
5. Vypočítajte bodový súčin vektorov
6. Nájdite uhol medzi vektormi

Do týchto 6 bodov samozrejme nespadá celá súradnicová metóda. Leží v srdci takej vedy, ako je analytická geometria, s ktorou sa zoznámite na univerzite. Chcem len postaviť základ, ktorý vám umožní riešiť problémy v jednom štáte. skúška. Úlohy časti B sme zistili v roku Teraz je čas prejsť na kvalitatívne novú úroveň! Tento článok bude venovaný metóde riešenia týchto problémov C2, v ktorej by bolo rozumné prejsť na metódu súradníc. Táto racionalita je daná tým, čo je potrebné v probléme nájsť a aký údaj je daný. Preto by som použil súradnicovú metódu, ak otázky sú:

1. Nájdite uhol medzi dvoma rovinami
2. Nájdite uhol medzi čiarou a rovinou
3. Nájdite uhol medzi dvoma rovnými čiarami
4. Nájdite vzdialenosť od bodu k rovine
5. Nájdite vzdialenosť od bodu k priamke
6. Nájdite vzdialenosť od priamky k rovine
7. Nájdite vzdialenosť medzi dvoma rovnými čiarami

Ak je údaj uvedený vo vyhlásení o probléme revolučným telesom (guľa, valec, kužeľ ...)

Vhodné tvary pre súradnicovú metódu sú:

1. Obdĺžnikový rovnobežnosten
2. Pyramída (trojuholníková, štvoruholníková, šesťhranná)

Tiež podľa mojich skúseností nie je vhodné používať súradnicovú metódu na:

1. Nájdenie prierezových oblastí
2. Výpočet objemu telies

Ihneď však treba poznamenať, že tri situácie „nepriaznivé“ pre metódu súradníc sú v praxi dosť zriedkavé. Vo väčšine úloh sa však môže stať vašim záchrancom, najmä ak nie ste príliš silní v trojrozmerných konštrukciách (ktoré sú niekedy dosť zložité).

Aké sú všetky údaje, ktoré som uviedol vyššie? Už nie sú ploché, napríklad ako štvorec, trojuholník, kruh, ale sú trojrozmerné! Preto musíme brať do úvahy nie dvojrozmerný, ale trojrozmerný súradnicový systém. Je postavený celkom ľahko: len okrem osí x a osí uvedieme ešte jednu os, os aplikácie. Obrázok schematicky ukazuje ich relatívnu polohu:

Všetky sú navzájom kolmé, pretínajú sa v jednom bode, ktorý budeme nazývať pôvod. Osa x, ako predtým, bude označená, os osi -a zadaná os aplikácie -.

Ak bol predtým každý bod v rovine charakterizovaný dvoma číslami - osou x a súradnicou, potom je každý bod v priestore už popísaný tromi číslami - os x, súradnica, aplikácia. Napríklad:

Preto je osa bodu rovnaká, súradnica je a aplikácia je.

Niekedy sa os x bodu nazýva aj premietanie bodu na os x, os ordinate je premietnutie bodu na os osy a aplikácia je premietnutie bodu na os aplikace. Ak je teda určený bod, potom bod so súradnicami:

sa nazýva projekcia bodu do roviny

sa nazýva projekcia bodu do roviny

Vyvstáva prirodzená otázka: sú všetky vzorce odvodené pre dvojrozmerný prípad platné vo vesmíre? Odpoveď je áno, sú férové ​​a vyzerajú rovnako. Pre malý detail. Myslím, že už si uhádol, pre ktorý. Do všetkých vzorcov budeme musieť pridať ešte jeden výraz, ktorý je zodpovedný za os aplikácie. Totiž.

1. Ak sú uvedené dva body :, potom:

• Vektorové súradnice:
• Vzdialenosť medzi dvoma bodmi (alebo dĺžkou vektora)
• Stred segmentu má súradnice

2. Ak sú uvedené dva vektory: a, potom:

• Ich bodový produkt je:
• Kosínus uhla medzi vektormi je:

Priestor však nie je taký jednoduchý. Dokážete si asi predstaviť, že pridanie ďalšej súradnice zavádza značnú rozmanitosť v spektre postáv „žijúcich“ v tomto priestore. A pre ďalšie rozprávanie budem musieť predstaviť určité, zhruba povedané, „zovšeobecnenie“ priamky. Táto „generalizácia“ je rovina. Čo vieš o lietadle? Skúste si odpovedať na otázku, čo je lietadlo? Je veľmi ťažké povedať. Všetci však máme intuitívnu predstavu o tom, ako to vyzerá:

Zhruba povedané, toto je akýsi nekonečný „listový“ vraz do vesmíru. „Nekonečno“ by malo byť chápané tak, že rovina sa rozprestiera vo všetkých smeroch, to znamená, že jej plocha sa rovná nekonečnu. Toto vysvetlenie „na prstoch“ však neposkytuje ani najmenšiu predstavu o štruktúre lietadla. A bude nás to zaujímať.

Pripomeňme si jeden zo základných axiómov geometrie:

• rovná čiara prechádza dvoma rôznymi bodmi v rovine, navyše iba jedným:

Alebo jeho náprotivok vo vesmíre:

Samozrejme si pamätáte, ako odvodiť rovnicu priamky z dvoch daných bodov, nie je to vôbec ťažké: ak má prvý bod súradnice: a druhý, rovnica priamky bude nasledovná:

Tým ste si prešli v 7. ročníku. V priestore vyzerá rovnica priamky takto: majme dva body so súradnicami :, potom rovnica priamky, ktorá nimi prechádza, má tvar:

Napríklad bodmi prechádza rovná čiara:

Ako to treba chápať? Malo by byť chápané nasledovne: bod leží na priamke, ak jeho súradnice vyhovujú nasledujúcemu systému:

Rovnica priamky nás nebude veľmi zaujímať, ale musíme si dať pozor na veľmi dôležitý koncept smerujúceho vektora priamky. - akýkoľvek nenulový vektor ležiaci na danej čiare alebo rovnobežnej s ňou.

Oba vektory sú napríklad smerové vektory priamky. Nech je bod ležiaci na priamke a je jeho smerovým vektorom. Potom môže byť rovnica priamky zapísaná v nasledujúcej forme:

Opäť ma nebude veľmi zaujímať rovnica priamky, ale naozaj potrebujem, aby ste si pamätali, čo je to smerový vektor! Opäť: je to ľubovoľný nenulový vektor ležiaci na priamke alebo rovnobežne s ňou.

Odstúpiť rovnica roviny v troch daných bodoch už nie je také triviálne a zvyčajne sa táto problematika v kurze nenachádza stredná škola... Ale márne! Táto technika je životne dôležitá, keď na riešenie zložitých problémov používame súradnicovú metódu. Predpokladám však, že sa chcete dozvedieť niečo nové? Okrem toho budete môcť na svojho učiteľa na univerzite zapôsobiť, keď sa ukáže, že už viete, ako na to s metodikou, ktorá sa zvyčajne študuje v rámci analytickej geometrie. Začnime teda.

Rovnica roviny sa príliš nelíši od rovnice priamky v rovine, konkrétne má tvar:

niektoré čísla (nie všetky sa rovnajú nule), ale premenné, napríklad: atď. Ako vidíte, rovnica roviny sa veľmi nelíši od rovnice priamky (lineárna funkcia). Pamätáte si však, čo sme si povedali? Povedali sme, že ak máme tri body, ktoré neležia na jednej priamke, tak je rovnica roviny z nich jedinečne zrekonštruovaná. Ale ako? Skúsim ti to vysvetliť.

Pretože rovnica roviny má tvar:

Body patria do tejto roviny, potom pri substitúcii súradníc každého bodu do rovnice roviny by sme mali získať správnu identitu:

Preto je potrebné vyriešiť tri rovnice aj s neznámymi! Dilema! Môžete to však vždy predpokladať (na to je potrebné rozdeliť). Získame teda tri rovnice s tromi neznámymi:

Takýto systém však nevyriešime, ale napíšeme záhadný výraz, ktorý z neho vyplýva:

Rovnica roviny prechádzajúcej tromi danými bodmi

\ [\ vľavo | (\ begin (pole) (* (20) (c)) (x - (x_0)) & ((x_1) - (x_0)) & ((x_2) - (x_0)) \\ (y - (y_0) ) & ((y_1) - (y_0)) & ((y_2) - (y_0)) \\ (z - (z_0)) & ((z_1) - (z_0)) & ((z_2) - (z_0)) \ end (pole)) \ vpravo | = 0 \]

Prestaň! Čo to je? Veľmi neobvyklý modul! Objekt, ktorý vidíte pred sebou, však nemá s modulom nič spoločné. Tento objekt sa nazýva determinant tretieho rádu. Keď sa odteraz budete zaoberať metódou súradníc v rovine, veľmi často sa stretnete s tými istými determinantmi. Čo je to determinant tretieho rádu? Zvláštne je, že je to len číslo. Zostáva pochopiť, aké konkrétne číslo porovnáme s determinantom.

Najprv si napíšeme determinant tretieho rádu vo viacerých všeobecný pohľad:

Kde sú nejaké čísla? Prvým indexom navyše rozumieme číslo riadku a indexom - číslo stĺpca. Napríklad to znamená, že dané číslo je na priesečníku druhého riadka a tretieho stĺpca. Položme si nasledujúcu otázku: ako presne budeme počítať taký determinant? To znamená, aké konkrétne číslo mu priradíme? Pre determinant tretieho rádu existuje heuristické (vizuálne) pravidlo trojuholníka, ktoré vyzerá nasledovne:

1. Súčin prvkov hlavnej uhlopriečky (z ľavého horného rohu do pravého dolného rohu) súčin prvkov tvoriacich prvý trojuholník „kolmo“ na hlavný diagonálny súčin prvkov tvoriacich druhý trojuholník „kolmo“ na hlavnú uhlopriečka
2. Súčin prvkov bočnej uhlopriečky (od pravého horného rohu k dolnému ľavému dolnému rohu) súčin prvkov tvoriacich prvý trojuholník „kolmo“ na bočný diagonálny súčin prvkov tvoriacich druhý trojuholník „kolmo“ na stranu uhlopriečka
3. Potom je determinant rovný rozdielu medzi hodnotami získanými v kroku a

Ak to všetko napíšeme do čísel, dostaneme nasledujúci výraz:

Napriek tomu nie je potrebné, aby ste si výpočetnú metódu v tejto forme zapamätali, stačí, ak budete mať v hlave trojuholníky a samotná predstava o tom, čo sa k čomu pridáva a čo sa potom od čoho odpočíta).

Ilustrujeme metódu trojuholníka na príklade:

1. Vypočítajte determinant:

Poďme zistiť, čo pridáme a čo odčítame:

Výrazy, ktoré majú „plus“:

Toto je hlavná uhlopriečka: súčin prvkov je

Prvý trojuholník „kolmý na hlavnú uhlopriečku: súčin prvkov je

Druhý trojuholník „kolmý na hlavnú uhlopriečku: súčin prvkov je

Pridajte tri čísla:

Výrazy, ktoré majú „mínus“

Toto je bočná uhlopriečka: súčin prvkov je

Prvý trojuholník „kolmý na bočnú uhlopriečku: súčin prvkov je

Druhý trojuholník „kolmý na bočnú uhlopriečku: súčin prvkov je

Pridajte tri čísla:

Zostáva iba odčítať od súčtu plusových výrazov súčet mínusových výrazov:

Preto

Ako vidíte, na výpočte determinantov tretieho rádu nie je nič zložité a nadprirodzené. Je dôležité pamätať si na trojuholníky a nerobiť aritmetické chyby. Teraz to skúste vypočítať sami:

Kontrolujeme:

1. Prvý trojuholník kolmý na hlavnú uhlopriečku:
2. Druhý trojuholník kolmý na hlavnú uhlopriečku:
3. Súčet výrazov s plusom:
4. Prvý trojuholník kolmý na bočnú uhlopriečku:
5. Druhý trojuholník kolmý na bočnú uhlopriečku:
6. Súčet výrazov s mínusom:
7. Súčet výrazov s plusom mínus súčet výrazov s mínusom:

Tu je niekoľko ďalších determinantov, vypočítajte si ich hodnoty sami a porovnajte ich s odpoveďami:

Odpovede:

No, zhodovalo sa to všetko? Super, potom môžeš ísť ďalej! Ak existujú problémy, moja rada je nasledovná: na internete je veľa programov na výpočet determinantu online. Všetko, čo potrebujete, je prísť s vlastným determinantom, vypočítať ho sami a potom ho porovnať s tým, čo program vypočíta. A tak ďalej, až kým sa výsledky nezačnú zhodovať. Som si istý, že tento okamih na seba nenechá dlho čakať!

Teraz sa vráťme k determinantu, ktorý som napísal, keď som hovoril o rovnici roviny prechádzajúcej tromi danými bodmi:

Všetko, čo potrebujete, je vypočítať jeho hodnotu priamo (pomocou metódy trojuholníkov) a výsledok nastaviť na nulu. Prirodzene, pretože ide o premenné, získate nejaký výraz, ktorý na nich závisí. Práve tento výraz bude rovnicou roviny prechádzajúcej tromi danými bodmi, ktoré neležia na jednej priamke!

Ukážme to na jednoduchom príklade:

1. Zostrojte rovnicu roviny prechádzajúcej bodmi

Determinant zostavujeme pre tieto tri body:

Zjednodušenie:

Teraz to vypočítame priamo podľa pravidla trojuholníkov:

\ [(\ left | (\ begin (pole) (* (20) (c)) (x + 3) & 2 & 6 \\ (y - 2) & 0 & 1 \\ (z + 1) & 5 & 0 \ end (pole)) \ right | = \ left ((x + 3) \ right) \ cdot 0 \ cdot 0 + 2 \ cdot 1 \ cdot \ left ((z + 1) \ right) + \ left ((y - 2) \ vpravo) \ cdot 5 \ cdot 6 -) \]

Rovnica roviny prechádzajúcej bodmi má teda tvar:

Teraz sa pokúste vyriešiť jeden problém sami a potom o ňom budeme diskutovať:

2. Nájdite rovnicu roviny prechádzajúcej bodmi

Teraz poďme diskutovať o riešení:

Zostavujeme determinant:

A vypočítame jeho hodnotu:

Potom má rovnica roviny tvar:

Alebo znížením o dostaneme:

Teraz dve úlohy pre sebaovládanie:

1. Zostrojte rovnicu roviny prechádzajúcej tromi bodmi:

Odpovede:

Všetko sa to zhodovalo? Opäť, ak existujú určité ťažkosti, potom moja rada znie: z hlavy vezmete tri body (s vysokým stupňom pravdepodobnosti nebudú ležať na tej istej priamke) a postavíte pozdĺž nich rovinu. A potom sa skontrolujete online. Napríklad na webe:

Pomocou determinantov však zostrojíme nielen rovnicu roviny. Nezabudnite, povedal som vám, že pre vektory nie je definovaný iba bodový produkt. Existuje tiež vektorový produkt, ako aj zmiešaný produkt. A ak je bodovým súčinom dvoch vektorov číslo, potom vektorovým súčinom dvoch vektorov bude vektor a tento vektor bude kolmý na dané:

Jeho modul sa navyše bude rovnať oblasti rovnobežníka postaveného na vektoroch a. Tento vektor budeme potrebovať na výpočet vzdialenosti od bodu k priamke. Ako vypočítame krížový súčin vektorov a ak sú uvedené ich súradnice? Determinant tretieho rádu nám opäť prichádza na pomoc. Predtým, ako prejdem k algoritmu na výpočet vektorového súčinu, však musím urobiť malú lyrickú odbočku.

Táto odchýlka sa týka bázových vektorov.

Schematicky sú znázornené na obrázku:

Prečo si myslíte, že sa im hovorí základné? Faktom je, že:

Alebo na obrázku:

Platnosť tohto vzorca je zrejmá, pretože:

Vektorový produkt

Teraz môžem začať predstavovať krížový produkt:

Vektorový súčin dvoch vektorov je vektor, ktorý sa vypočíta podľa nasledujúceho pravidla:

Teraz uvedieme niekoľko príkladov výpočtu krížového produktu:

Príklad 1: Nájdite krížový súčin vektorov:

Riešenie: Zostavujem determinant:

A vypočítam to:

Teraz, od zápisu, pokiaľ ide o základné vektory, sa vrátim k obvyklému zápisu vektora:

Preto:

Teraz to vyskúšajte.

Pripravený? Kontrolujeme:

A tradične dve úlohy na ovládanie:

1. Nájdite krížový súčin nasledujúcich vektorov:
2. Nájdite krížový súčin nasledujúcich vektorov:

Odpovede:

Zmiešaný produkt troch vektorov

Posledná konštrukcia, ktorú potrebujem, je zmiešaný súčin troch vektorov. Rovnako ako skalárne číslo je to číslo. Existujú dva spôsoby výpočtu. - prostredníctvom determinantu, - prostredníctvom zmiešaného produktu.

Menujme teda tri vektory:

Potom zmiešaný súčin troch vektorov, označených, možno vypočítať ako:

1. - to znamená, že zmiešaný produkt je bodový produkt vektora krížovým súčinom dvoch ďalších vektorov

Napríklad zmiešaný produkt troch vektorov je:

Skúste to vypočítať sami pomocou krížového produktu a uistite sa, že sa výsledky zhodujú!

A opäť - dva príklady nezávislého riešenia:

Odpovede:

Výber súradnicového systému

Teraz máme všetky potrebné základy znalostí na riešenie zložitých stereometrických problémov v geometrii. Myslím si však, že skôr, ako prejdeme priamo k príkladom a algoritmom na ich riešenie, bude užitočné zaoberať sa ďalšou otázkou: ako presne vyberte súradnicový systém pre konkrétny obrázok. Koniec koncov, je to práve voľba relatívnej polohy súradnicového systému a obrázku v priestore, ktoré v konečnom dôsledku určia, aké ťažkopádne budú výpočty.

Pripomínam, že v tejto časti sa pozrieme na nasledujúce tvary:

1. Obdĺžnikový rovnobežnosten
2. Rovný hranol (trojuholníkový, šesťhranný ...)
3. Pyramída (trojuholníková, štvoruholníková)
4. Tetrahedron (rovnaký ako trojuholníková pyramída)

Pre obdĺžnikový box alebo kocku vám odporúčam nasledujúcu konštrukciu:

To znamená, že postavím figúrku „do rohu“. Kocka a rovnobežnosten sú veľmi pekné tvary. Vždy pre nich môžete ľahko nájsť súradnice jeho vrcholov. Napríklad, ak (ako je znázornené na obrázku)

potom súradnice vrcholov sú nasledujúce:

Toto si samozrejme nemusíte pamätať, ale pamätajte si, ako najlepšie umiestniť kocku resp obdĺžnikový rovnobežnosten- žiaduce.

Rovný hranol

Hranol je škodlivejšia postava. V priestore môže byť umiestnená rôznymi spôsobmi. Nasledujúca možnosť sa mi však zdá najprijateľnejšia:

Trojuholníkový hranol:

To znamená, že jednu zo strán trojuholníka umiestnime úplne na os a jeden z vrcholov sa zhoduje s počiatkom.

Šesťhranný hranol:

To znamená, že jeden z vrcholov sa zhoduje s počiatkom a jedna zo strán leží na osi.

Štvorhranná a šesťhranná pyramída:

Situácia podobná kocke: zarovnajte dve strany základne so súradnicovými osami, zarovnajte jeden z vrcholov so začiatkom. Jedinou menšou obtiažnosťou bude vypočítať súradnice bodu.

Pre šesťhrannú pyramídu - to isté ako pre šesťhranný hranol. Hlavnou úlohou bude opäť nájsť súradnice vrcholu.

Trojsten (pyramída)

Situácia je veľmi podobná tej, ktorú som uviedol pre trojuholníkový hranol: jeden vrchol sa zhoduje s počiatkom, jedna strana leží na súradnicovej osi.

Teraz sme sa ty a ja konečne blízko k riešeniu problémov. Z toho, čo som povedal na samom začiatku článku, by ste mohli vyvodiť nasledujúci záver: väčšina problémov C2 je rozdelená do 2 kategórií: rohové problémy a problémy so vzdialenosťou. Najprv sa budeme zaoberať problémom nájdenia uhla. Na druhej strane sú rozdelení do nasledujúcich kategórií (so zvyšujúcou sa obtiažnosťou):

Hľadanie rohov

1. Nájdenie uhla medzi dvoma rovnými čiarami
2. Zistenie uhla medzi dvoma rovinami

Uvažujme o týchto úlohách postupne: začnite hľadaním uhla medzi dvoma rovnými čiarami. Pamätajte si, neriešili sme predtým ja a ja podobné príklady? Pamätajte si, že už sme niečo podobné mali ... Hľadali sme uhol medzi dvoma vektormi. Pripomeniem vám, ak sú uvedené dva vektory: a, potom je uhol medzi nimi zistený z pomeru:

Teraz máme cieľ - nájsť uhol medzi dvoma rovnými čiarami. Prejdeme k „plochému obrázku“:

Koľko uhlov sme dostali, keď sa pretínajú dve rovné čiary? Toľko vecí. Je pravda, že iba dvaja z nich nie sú rovnakí, zatiaľ čo iní sú k nim zvislí (a preto sa s nimi zhodujú). Aký uhol by sme teda mali vziať do úvahy uhol medzi dvoma rovnými čiarami: alebo? Tu platí pravidlo: uhol medzi dvoma rovnými čiarami nie je vždy väčší ako stupne... To znamená, že z dvoch uhlov vždy zvolíme uhol s najmenšou mierou stupňa. To znamená, že na tomto obrázku je uhol medzi dvoma rovnými čiarami rovnaký. Aby sa zakaždým neobťažovali s hľadaním najmenšieho z dvoch uhlov, prefíkaní matematici navrhli použiť modul. Uhol medzi dvoma rovnými čiarami je teda určený vzorcom:

Ako pozorný čitateľ ste si mali položiť otázku: Kde v skutočnosti vezmeme tieto čísla, ktoré potrebujeme na výpočet kosínusu uhla? Odpoveď: Prevezmeme ich zo smerových vektorov priamok! Algoritmus na nájdenie uhla medzi dvoma rovnými čiarami je teda nasledujúci:

1. Aplikujeme vzorec 1.

Alebo podrobnejšie:

1. Hľadáme súradnice smerového vektora prvej priamky
2. Hľadáme súradnice smerového vektora druhej priamky
3. Vypočítajte modul ich bodového súčinu
4. Hľadáme dĺžku prvého vektora
5. Hľadáme dĺžku druhého vektora
6. Vynásobte výsledky z bodu 4 výsledkami z bodu 5
7. Výsledok bodu 3 delíme výsledkom bodu 6. Dostaneme kosínus uhla medzi čiarami
8. Ak vám tento výsledok umožní presne vypočítať uhol, hľadajte ho
9. V opačnom prípade píšeme cez inverzný kosínus

Teraz je čas prejsť k problémom: Podrobne predvediem riešenie prvých dvoch, v krátkej forme predstavím riešenie ďalšieho a na posledné dva problémy uvediem iba odpovede, všetky výpočty za ne musíte vykonať sami.

Úlohy:

1. V správnom uhle tet-ra-ed-re nay-di-those medzi vami-tak-že tet-ra-ed-ra a tvárou med-di-a-noy bo-kovy.

2. V pravostrannom šesťuhoľnom noy pi-ra-mi-de sú strany os-no-va-nia rovnaké a rebrá sú rovnaké, nájdite uhol medzi rovnými čiarami a.

3. Dĺžky všetkých rebier správneho štvor-ty-rekh-uhlia pi-ra-mi-dy sú si navzájom rovnaké. Nay-di-those uhol medzi rovnými čiarami a ak od-cut je you-co-that given pi-ra-mi-dy, point is se-re-di-na her bo-ko- second rib

4. Na okraji kocky od bodu-me-che-na tak, aby Nay-di-te bol uhol medzi priamkami a

5. Bod-se-re-di-na hranách kocky Nay-di-te uhol medzi priamkami a.

Nie je náhoda, že som úlohy zoradil v tomto poradí. Aj keď ste ešte nemali čas začať sa orientovať v metóde súradníc, sám analyzujem „najproblematickejšie“ figúry a nechám vás, aby ste sa vysporiadali s najjednoduchšou kockou! Postupne sa budete musieť naučiť pracovať so všetkými figúrkami; Zvýším komplexnosť úloh z témy na tému.

Začnime riešiť problémy:

1. Nakreslite štvorsten a umiestnite ho do súradnicového systému, ako som už naznačil. Pretože je tetrahedron pravidelný, všetky jeho tváre (vrátane základne) sú pravidelnými trojuholníkmi. Keďže nie je daná dĺžka strany, môžem to brať rovnako. Myslím, že chápete, že uhol nebude v skutočnosti závisieť od toho, ako veľmi bude náš štvorsten „natiahnutý“? Nakreslím tiež výšku a medián do štvorstena. Cestou nakreslím jeho základňu (bude sa nám to tiež hodiť).

Potrebujem nájsť uhol medzi a. Čo vieme? Poznáme iba súradnicu bodu. To znamená, že stále potrebujeme nájsť súradnice bodov. Teraz si myslíme: bod je priesečníkom výšok (alebo stredov alebo stredov) trojuholníka. Bod je vyvýšený bod. Bod je stred segmentu. Potom konečne musíme nájsť: súradnice bodov :.

Začnime tým najjednoduchším: súradnice bodu. Pozrite sa na obrázok: Je zrejmé, že aplikácia bodu je nulová (bod leží na rovine). Jeho súradnica je (pretože - medián). Je ťažšie nájsť jej os x. To sa však dá ľahko vykonať na základe Pytagorovej vety: Uvažujme o trojuholníku. Jeho prepona je rovnaká a jedna z nôh je rovnaká Potom:

Nakoniec tu máme :.

Teraz nájdeme súradnice bodu. Je zrejmé, že jeho aplikácia je opäť rovná nule a jeho súradnica je rovnaká ako v bode, to znamená. Nájdeme jeho os x. Ak si to pamätáte, robí sa to celkom triviálne výšky rovnostranného trojuholníka sú proporcionálne delené priesečníkom počítanie od vrchu. Pretože :, potom sa požadovaná os x bodu, rovná dĺžke segmentu, rovná :. Súradnice bodu sú teda rovnaké:

Nájdeme súradnice bodu. Je zrejmé, že jeho os x a súradnica sa zhodujú s osou x a súradnicou bodu. A aplikácia sa rovná dĺžke segmentu. - toto je jedna z nôh trojuholníka. Prepona trojuholníka je segment - noha. Hľadá sa z úvah, ktoré som zvýraznil tučným písmom:

Bod je stredný bod priamky. Potom si musíme zapamätať vzorec pre súradnice stredového bodu segmentu:

To je všetko, teraz môžeme vyhľadať súradnice smerových vektorov:

Všetko je pripravené: všetky údaje nahradíme vzorcom:

Preto

Odpoveď:

Nemali by ste sa báť takýchto „strašidelných“ odpovedí: pri problémoch s C2 je to bežná prax. Skôr by ma prekvapila „milá“ odpoveď v tejto časti. Ako ste si tiež všimli, prakticky som sa neuchýlil k ničomu inému ako k Pytagorovej vete a k vlastnosti výšok rovnostranného trojuholníka. To znamená, že na vyriešenie stereometrického problému som použil úplne minimum stereometrie. Zisk v tomto je čiastočne „uhasený“ dosť ťažkopádnymi výpočtami. Ale sú dosť algoritmické!

2. Nakreslime pravidelnú šesťuholníkovú pyramídu spolu so súradnicovým systémom a tiež jej základňou:

Musíme nájsť uhol medzi čiarami a. Preto je naša úloha obmedzená na nájdenie súradníc bodov :. Z malého obrázku nájdeme súradnice posledných troch a prostredníctvom súradnice bodu nájdeme súradnicu vrcholu. Pracujte hromadne, ale musíte to začať!

a) Súradnica: je zrejmé, že jej aplikácia a súradnica sa rovnajú nule. Poďme nájsť os x. Za týmto účelom zvážte pravouhlý trojuholník. Bohužiaľ, v ňom poznáme iba preponu, ktorá sa rovná. Pokúsime sa nájsť nohu (pretože je zrejmé, že zdvojnásobená dĺžka nohy nám poskytne osu bodu). Ako ju môžeme nájsť? Pamätajme si, akú postavu máme na základni pyramídy? Toto je pravidelný šesťuholník. Čo to znamená? To znamená, že má všetky strany a všetky uhly. Mal by som nájsť jeden taký kútik. Nejaké nápady? Existuje veľa myšlienok, ale existuje vzorec:

Súčet uhlov pravidelného n-uholníka je .

Súčet uhlov pravidelného šesťuholníka sa teda rovná stupňom. Potom je každý z uhlov rovný:

Znova sa pozrieme na obrázok. Je zrejmé, že segment je úsečkou uhla. Potom je uhol rovný stupňom. Potom:

Potom kde.

Má teda súradnice

b) Teraz môžeme ľahko nájsť súradnicu bodu :.

c) Nájdite súradnice bodu. Pretože jeho os x sa zhoduje s dĺžkou segmentu, rovná sa. Nájdenie súradnice tiež nie je veľmi ťažké: ak spojíme body a označíme priesečník priamky, povedzme, pomocou. (DIY jednoduchá konštrukcia). Potom je súradnica bodu B rovná súčtu dĺžok segmentov. Pozrime sa znova na trojuholník. Potom

Potom od Potom má bod súradnice

d) Teraz nájdeme súradnice bodu. Uvažujme obdĺžnik a dokážme, že súradnice bodu sú teda:

e) Zostáva nájsť súradnice vrcholu. Je zrejmé, že jeho os x a súradnica sa zhodujú s osou x a súradnicou bodu. Poďme nájsť aplikátor. Odvtedy. Uvažujme pravouhlý trojuholník. Vyjadrením problému je bočný okraj. Toto je prepona môjho trojuholníka. Potom je výška pyramídy nohou.

Potom má bod súradnice:

V poriadku, mám pre mňa súradnice všetkých bodov záujmu. Hľadanie súradníc smerových vektorov priamok:

Hľadáme uhol medzi týmito vektormi:

Odpoveď:

Pri riešení tohto problému som opäť nepoužil žiadne sofistikované triky, okrem vzorca pre súčet uhlov pravidelného n-uholníka, ako aj určovania kosínusu a sínusu pravouhlého trojuholníka.

3. Keďže nám opäť nie sú dané dĺžky rebier v pyramíde, budem ich považovať za rovné jednému. Pretože VŠETKY hrany, a nielen bočné, sú si navzájom rovnaké, potom na základni pyramídy a mňa leží štvorec a bočné plochy sú pravidelnými trojuholníkmi. Nakreslíme takú pyramídu a jej základňu do roviny a označíme všetky údaje uvedené v texte problému:

Hľadáme uhol medzi a. Pri hľadaní súradníc bodov urobím veľmi krátke výpočty. Budete ich musieť „dešifrovať“:

b) - stred segmentu. Jeho súradnice:

c) Dĺžku segmentu nájdem podľa Pytagorovej vety v trojuholníku. Nájdem ho v trojuholníku podľa Pytagorovej vety.

Súradnice:

d) - stred segmentu. Jeho súradnice sú rovnaké

e) Vektorové súradnice

f) Súradnice vektora

g) Hľadanie uhla:

Kocka je najjednoduchšia figúrka. Som si istý, že na to môžeš prísť sám. Odpovede na problémy 4 a 5 sú tieto:

Nájdenie uhla medzi priamkou a rovinou

Čas na jednoduché úlohy sa skončil! Teraz budú príklady ešte komplikovanejšie. Aby sme našli uhol medzi priamkou a rovinou, budeme postupovať nasledovne:

1. Z troch bodov zostrojíme rovnicu roviny
   ,
   pomocou determinantu tretieho rádu.
2. Súradnice smerujúceho vektora priamky hľadáme podľa dvoch bodov:
3. Na výpočet uhla medzi priamkou a rovinou použijeme vzorec:

Ako vidíte, tento vzorec je veľmi podobný tomu, ktorý sme použili na nájdenie uhlov medzi dvoma rovnými čiarami. Štruktúra pravej strany je rovnaká a na ľavej strane teraz hľadáme sínus, nie kosínus, ako predtým. Bola pridaná jedna škaredá akcia - hľadanie rovnice roviny.

Neodkladajme riešenie príkladov:

1. Os-no-va-ni-em direct-pri-we are-la-et-sy rovná-chudobná-re-ny trojuholníková-prezývka You-co-že ceny-sme si rovní. Nai di te uhol medzi rovným a plochým

2. V obdĺžnikovom pa-ra-le-le-pi-pe-de od západného Nay-di-te uhol medzi priamkou a rovinou

3. V správnom šesťuholníkovom hranole sú všetky hrany rovnaké. Nai-di-te je uhol medzi priamkou a rovinou.

4. V pravostrannom trojuholníku pi-ra-mi-de s os-no-va-ni-je od západu od rebier uhol Nay-di-te, ob-ra-zo-van -táto plochosť os-no-va-nia a rovné, pro-ho-dya-shi cez se-re-di-us rebier a

5. Dĺžky všetkých rebier pravej štvorhrannej pyramídy s vrcholom sú navzájom rovnaké. Nay-di-te je uhol medzi priamkou a rovinou, ak je bodom re-di-na-bo-ko-th rebrá pi-ra-mi-dy.

Opäť podrobne vyriešim prvé dva problémy, tretí - stručne a posledné dva nechám na vás, aby ste ich vyriešili sami. Navyše ste sa už zaoberali trojuholníkovým a štvoruholníkové pyramídy, ale s hranolmi - zatiaľ nie.

Riešenie:

1. Zobrazme hranol, ako aj jeho základ. Spojme to so súradnicovým systémom a označme všetky údaje uvedené vo vyhlásení o probléme:

Ospravedlňujem sa za určité nedodržanie proporcií, ale pre vyriešenie problému to v skutočnosti nie je také dôležité. Lietadlo je len „zadná stena“ môjho hranola. Je dosť ľahké uhádnuť, že rovnica takejto roviny má tvar:

Toto sa však dá priamo zobraziť:

Vyberieme ľubovoľné tri body v tejto rovine: napríklad.

Zostavme rovnicu roviny:

Cvičenie pre vás: vypočítajte si tento determinant sami. Urobil si to? Potom má rovnica roviny tvar:

Alebo jednoducho

Preto

Na vyriešenie príkladu musím nájsť súradnice smerového vektora priamky. Pretože bod sa zhodoval s počiatkom, súradnice vektora sa jednoducho zhodujú so súradnicami bodu. Na tento účel najskôr nájdeme súradnice bodu.

Za týmto účelom zvážte trojuholník. Nakreslite výšku (je to medián a úsečka) z vrcholu. Odvtedy je potom súradnica bodu rovná. Aby sme našli úsečku tohto bodu, musíme vypočítať dĺžku segmentu. Podľa Pythagorovej vety máme:

Potom má bod súradnice:

Bod je „zvýšený“ o bod:

Potom súradnice vektora:

Odpoveď:

Ako vidíte, pri riešení takýchto problémov nie je nič zásadne ťažké. V skutočnosti tento proces ďalej zjednodušuje „rovnosť“ tvaru, akým je hranol. Teraz prejdeme k ďalšiemu príkladu:

2. Nakreslite rovnobežnosten, nakreslite do neho rovinu a rovnú čiaru a tiež samostatne nakreslite jeho spodnú základňu:

Najprv nájdeme rovnicu roviny: Súradnice troch bodov v nej ležiace:

(Prvé dve súradnice boli získané zrejmým spôsobom a poslednú súradnicu môžete ľahko nájsť na obrázku z bodu). Potom zostavíme rovnicu roviny:

Vypočítame:

Hľadáme súradnice smerového vektora: Je zrejmé, že jeho súradnice sa zhodujú so súradnicami bodu, však? Ako zistím súradnice? Toto sú súradnice bodu, zdvihnuté pozdĺž osi aplikácie o jednu! ... Potom hľadáme požadovaný uhol:

Odpoveď:

3. Nakreslite pravidelnú šesťuholníkovú pyramídu a potom do nej nakreslite rovinu a rovnú čiaru.

Tu je dokonca aj nakreslenie roviny problematické, nehovoriac o riešení tohto problému, ale súradnicovej metóde je to jedno! Jeho univerzálna výhoda spočíva v univerzálnosti!

Lietadlo prechádza tromi bodmi :. Hľadáme ich súradnice:

jeden). Súradnice posledných dvoch bodov nakreslite sami. Riešenie problému so šesťhrannou pyramídou vám na to príde!

2) Zostavíme rovnicu roviny:

Hľadáme súradnice vektora :. (Pozrite sa znova na problém trojuholníkovej pyramídy!)

3) Hľadáme uhol:

Odpoveď:

Ako vidíte, na týchto úlohách nie je nič nadprirodzene ťažké. Len musíte byť veľmi opatrní s koreňmi. Na posledné dva problémy uvediem iba odpovede:

Ako vidíte, technika riešenia problémov je všade rovnaká: hlavnou úlohou je nájsť súradnice vrcholov a nahradiť ich do niektorých vzorcov. Zostáva nám zvážiť ešte jednu triedu problémov pri výpočte uhlov, a to:

Výpočet uhlov medzi dvoma rovinami

Algoritmus riešenia bude nasledujúci:

1. V troch bodoch hľadáme rovnicu prvej roviny:
2. Pre ďalšie tri body hľadáme rovnicu druhej roviny:
3. Použijeme vzorec:

Ako vidíte, vzorec je veľmi podobný dvom predchádzajúcim, pomocou ktorých sme hľadali uhly medzi priamkami a medzi priamkou a rovinou. Zapamätať si tento teda pre vás nebude ťažké. Prejdeme priamo k analýze úloh:

1. Sto ro-na os-no-va-nia pravostranného trojuholníkového hranola je rovnaké a priemer veľkej tváre je rovnaký. Nay-di-ti sú uhlom medzi rovinou a rovinou hranola.

2. V správnom štvoro-rek-uhli-noy pi-ra-mi-de, ktorého všetky hrany sú rovnaké, nájdite sínus uhla medzi rovinou a rovinou to-stu, pro-ho- dya-shchey cez bod per-pen-di-ku-lar-ale rovný.

3. V správnom hranole so štyrmi uhlami sú uhly os-no-va-nia rovnaké a strany sú rovnaké. Na okraji od-me-che-do bodu tak, aby. Nájdite uhol medzi rovinou a sti-mi a

4. V pravom štvorrohovom hranole sú strany os-no-va-nia rovnaké a bočné hrany sú rovnaké. Na okraji od-me-che-k bodu tak, aby Nay-di-te bol uhol medzi rovinou a st-mi a.

5. V kocke nay-di-te ko-si-nus uhla medzi rovinou-ko-sti-mi a

Riešenie problémov:

1. Nakreslím pravidelný (na základni - rovnostranný trojuholník) trojuholníkový hranol a označím na ňom roviny, ktoré sa objavujú vo vyhlásení o probléme:

Musíme nájsť rovnice dvoch rovín: Rovnica základne je triviálna: zodpovedajúci determinant môžete zostaviť z troch bodov, ale rovnicu zostavím naraz:

Teraz nájdeme rovnicu Bod má súradnice Bod - Pretože je to medián a výška trojuholníka, je ľahké ho nájsť v trojuholníku pomocou Pythagorovej vety. Potom má bod súradnice: Nájdite aplikáciu bodu. Za týmto účelom zvážte pravouhlý trojuholník

Potom získame nasledujúce súradnice: Vytvoríme rovnicu roviny.

Vypočítame uhol medzi rovinami:

Odpoveď:

2. Vytvorenie kresby:

Najťažšie je pochopiť, čo je táto záhadná rovina, prechádzajúca bodom kolmo. Hlavná vec je, čo je to? Hlavná vec je pozornosť! Čiara je skutočne kolmá. Rovná čiara je tiež kolmá. Potom bude rovina prechádzajúca týmito dvoma rovnými čiarami kolmá na priamu čiaru a mimochodom prejde bodom. Toto lietadlo prechádza aj vrcholom pyramídy. Potom hľadané lietadlo - A lietadlo nám už bolo dané. Hľadáme súradnice bodov.

Nájdite súradnicu bodu v bode. Z malého obrázku je ľahké vyvodiť, že súradnice bodu budú nasledujúce: Čo teraz treba nájsť, aby sme našli súradnice vrcholu pyramídy? Musíte tiež vypočítať jeho výšku. To sa robí pomocou rovnakej Pythagorovej vety: najskôr to dokážte (triviálne z malých trojuholníkov tvoriacich štvorec na základni). Pretože podľa podmienky máme:

Teraz je všetko pripravené: súradnice vrcholu:

Zostavíme rovnicu roviny:

Ste už špeciálni vo výpočte determinantov. Môžete ľahko získať:

Alebo inak (ak vynásobíme obe časti koreňom dvoch)

Teraz nájdeme rovnicu roviny:

(Nezabudli ste, ako dostaneme rovnicu roviny, že? Ak nerozumiete, odkiaľ pochádza táto mínusová rovnica, vráťte sa k definícii rovnice roviny! Vždy sa ukázalo, že pôvod súradníc patril môjmu lietadlu!)

Vypočítame determinant:

(Vidíte, že rovnica roviny sa zhoduje s rovnicou priamky prechádzajúcou bodmi a! Zamyslite sa prečo!)

Teraz vypočítame uhol:

Musíme nájsť sínus:

Odpoveď:

3. Zložitá otázka: čo je podľa vás obdĺžnikový hranol? Je to len rovnobežnosten, ktorý dobre poznáte! Okamžite urobíme kresbu! Je dokonca možné nezobrazovať základňu oddelene, tu je malý prínos:

Rovina, ako sme už uviedli, je napísaná vo forme rovnice:

Teraz tvoríme lietadlo

Okamžite zostavíme rovnicu roviny:

Hľadáme uhol:

Teraz odpovede na posledné dva problémy:

Teraz je čas na prestávku, pretože vy a ja sme skvelí a odviedli sme skvelú prácu!

Súradnice a vektory. Pokročilá úroveň

V tomto článku s vami prediskutujeme ďalšiu triedu problémov, ktoré je možné vyriešiť súradnicovou metódou: problémy so vzdialenosťou. Konkrétne zvážime nasledujúce prípady:

1. Výpočet vzdialenosti medzi prekríženými čiarami.

Tieto úlohy som si objednal, pretože sa zvyšuje ich zložitosť. Ukazuje sa, že je najľahšie nájsť vzdialenosť od bodu k rovine, a najťažšie je nájsť ho vzdialenosť medzi križujúcimi sa čiarami... Aj keď, samozrejme, nič nie je nemožné! Neodkladajme to a okamžite pristúpime k zváženiu prvej triedy problémov:

Výpočet vzdialenosti od bodu k rovine

Čo potrebujeme na vyriešenie tohto problému?

1. Súradnice bodu

Hneď ako získame všetky potrebné údaje, použijeme vzorec:

Už by ste mali vedieť, ako zostavíme rovnicu roviny z predchádzajúcich problémov, o ktorých som hovoril v minulej časti. Hneď sa pustíme do úloh. Schéma je nasledovná: 1, 2, pomôžem vám vyriešiť a podrobne 3, 4 - iba odpoveď, rozhodnete sa sami a porovnáte. Začnime!

Úlohy:

1. Vzhľadom na kocku. Dĺžka okraja kocky je. Nay-di-te distance-i-ni from se-re-di-us from-cut to flat-to-sti

2. Vzhľadom na pravú-vil-naya štyri-ty-rekh-uhlie-naya pi-ra-mi-da Bo-kovoe hrana side-ro-na os-no-va-nia je rovnaká. Nay-di-tie vzdialenosť od bodu k rovine-k-sti, kde-se-re-di-on rebrá.

3. V pravostrannom trojuholníku pi-ra-mi-de s os-no-va-ni je bo-k-tý okraj rovnaký a strana-ro-na je-no-va- sa rovná . Vzdialenosť Nay-di-te od vrcholu k rovine.

4. V správnom šesťuholníkovom hranole sú všetky hrany rovnaké. Vzdialenosť medzi bodom a lietadlom nie je.

Riešenie:

1. Nakreslite kocku s hranami jednotiek, zostrojte segment a rovinu, stred segmentu označte písmenom

.

Najprv začnime s ľahkosťou: nájdite súradnice bodu. Odvtedy (pamätajte si súradnice stredového bodu segmentu!)

Teraz zostavíme rovnicu roviny podľa troch bodov

\ [\ vľavo | (\ begin (array) (* (20) (c)) x & 0 & 1 \\ y & 1 & 0 \\ z & 1 & 1 \ end (array)) \ right | = 0 \]

Teraz môžem začať hľadať vzdialenosť:

2. Začnite znova kresbou, na ktorú označíme všetky údaje!

Pre pyramídu by pomohlo nakresliť jej základňu oddelene.

Dokonca aj skutočnosť, že kreslím ako kura s labkou, nám nebráni v jednoduchom vyriešení tohto problému!

Teraz je ľahké nájsť súradnice bodu

Pretože súradnice bodu, potom

2. Pretože súradnice bodu a sú stredovým bodom segmentu, potom

Ľahko nájdeme súradnice ďalších dvoch bodov v rovine. Zostavíme rovnicu roviny a zjednodušíme ju:

\ [\ vľavo | (\ left | (\ begin (pole) (* (20) (c)) x & 1 & (\ frac (3) (2)) \\ y & 0 & (\ frac (3) (2)) \ \ z & 0 & (\ frac ((\ sqrt 3)) (2)) \ end (pole)) \ right |) \ right | = 0 \]

Pretože bod má súradnice:, vypočítame vzdialenosť:

Odpoveď (veľmi zriedkavá!):

No, prišiel na to? Zdá sa mi, že všetko je tu také technické ako v príkladoch, ktoré sme s vami zvažovali v predchádzajúcej časti. Som si teda istý, že ak ste tento materiál zvládli, nebude pre vás ťažké vyriešiť zostávajúce dva problémy. Dám len odpovede:

Výpočet vzdialenosti od priamky k rovine

V skutočnosti tu nie je nič nové. Ako je možné vzájomne umiestniť čiaru a rovinu? Majú všetky možnosti: pretínať sa alebo je priamka rovnobežná s rovinou. Aká je podľa vás vzdialenosť od priamky k rovine, s ktorou sa táto priamka pretína? Zdá sa mi, že tu je zrejmé, že takáto vzdialenosť sa rovná nule. Nezaujímavý prípad.

Druhý prípad je zložitejší: tu je vzdialenosť už nenulová. Pretože je však čiara rovnobežná s rovinou, potom je každý bod priamky v rovnakej vzdialenosti od tejto roviny:

Preto:

A to znamená, že moja úloha bola zredukovaná na predchádzajúcu: hľadáme súradnice akéhokoľvek bodu na priamke, hľadáme rovnicu roviny, počítame vzdialenosť od bodu k rovine. V skutočnosti sú tieto úlohy na skúške veľmi zriedkavé. Podarilo sa mi nájsť iba jeden problém a údaje v ňom boli také, že súradnicová metóda na neho nebola veľmi použiteľná!

Teraz prejdeme k ďalšej, oveľa dôležitejšej triede problémov:

Výpočet vzdialenosti bodu k priamke

Čo potrebujeme?

1. Súradnice bodu, od ktorého hľadáme vzdialenosť:

2. Súradnice akéhokoľvek bodu ležiaceho na priamke

3. Súradnice smerujúceho vektora priamky

Aký vzorec používame?

Čo pre vás znamená menovateľ tohto zlomku, a preto by malo byť zrejmé: toto je dĺžka smerujúceho vektora priamky. Tu je veľmi záludný čitateľ! Výraz znamená modul (dĺžka) vektorového súčinu vektorov a Ako vypočítať krížový súčin sme študovali v predchádzajúcej časti práce. Obnovte svoje znalosti, budú nám teraz veľmi užitočné!

Algoritmus na riešenie problémov bude teda nasledujúci:

1. Hľadáme súradnice bodu, od ktorého hľadáme vzdialenosť:

2. Hľadáme súradnice akéhokoľvek bodu na priamke, ku ktorej hľadáme vzdialenosť:

3. Zostavte vektor

4. Zostavte smerový vektor priamky

5. Vypočítajte krížový súčin

6. Hľadáme dĺžku výsledného vektora:

7. Vypočítajte vzdialenosť:

Máme veľa práce a príklady budú dosť zložité! Takže teraz zamerajte všetku svoju pozornosť!

1. Dana je pravo-vil-naya trojuholníkový pi-ra-mi-da s vrcholom. Sto-ro-na os-no-va-nia pi-ra-mi-dy je rovnaká, ty-tak-ktorá je rovnaká. Nay-di-those distance-i-nie from the se-re-di-ny of the bo-ko-th rib to the straight line, where points and are the se-re-di-ny of the rebres and so -od- veterinára-ale.

2. Dlžky rebier a pravouhlé pa-ral-le-le-le-pi-pe-da sú rovnaké, v uvedenom poradí, a vzdialenosť Nay-di-zhora nahor

3. V šesťruhovom hranole pre pravákov sú všetky okraje roje rovnaké ako vzdialenosť medzi bodom a priamkou.

Riešenie:

1. Vytvoríme úhľadný výkres, na ktorý označíme všetky údaje:

Máme s vami veľa práce! Najprv by som chcel slovami popísať, čo budeme hľadať a v akom poradí:

1. Súradnice bodov a

2. Súradnice bodu

3. Súradnice bodov a

4. Súradnice vektorov a

5. Ich krížový produkt

6. Dĺžka vektora

7. Dĺžka vektorového produktu

8. Vzdialenosť od do

Nuž, máme veľa práce! Pustíme sa do toho, vyhrnieme si rukávy!

1. Na nájdenie súradníc výšky pyramídy potrebujeme poznať súradnice bodu. Jeho aplikácia je rovná nule a súradnica je rovnaká ako Abscissa, rovná sa dĺžke segmentu. Pretože je výška rovnostranného trojuholníka, delí sa vo vzťahu a odteraz sa počíta zhora. Nakoniec sme dostali súradnice:

Súradnice bodov

2. - stred segmentu

3. - stred segmentu

Stred segmentu

4. Súradnice

Vektorové súradnice

5. Vypočítajte krížový produkt:

6. Dĺžka vektora: najľahšie sa zmení tak, že segment je stredná čiara trojuholníka, čo znamená, že sa rovná polovici základne. Takže.

7. Uvažujeme dĺžku vektorového súčinu:

8. Nakoniec nájdeme vzdialenosť:

Fuj, to je všetko! Úprimne povedané, riešenie tohto problému pomocou tradičných metód (prostredníctvom konštrukcií) by bolo oveľa rýchlejšie. Ale tu som všetko zredukoval na pripravený algoritmus! Myslím si, že algoritmus riešenia je vám jasný? Preto vás požiadam, aby ste zostávajúce dva problémy vyriešili sami. Porovnajme odpovede?

Opäť opakujem: je jednoduchšie (rýchlejšie) vyriešiť tieto problémy prostredníctvom konštrukcií a bez použitia súradnicovej metódy. Toto riešenie som predviedol len preto, aby som vám ukázal univerzálnu metódu, ktorá vám umožní „nič nedokončiť“.

Nakoniec zvážte poslednú triedu problémov:

Výpočet vzdialenosti medzi prekríženými čiarami

Algoritmus riešenia problémov tu bude podobný predchádzajúcemu. Čo máme:

3. Akékoľvek vektorové spojovacie body prvej a druhej priamky:

Ako zistíme vzdialenosť medzi rovnými čiarami?

Vzorec je nasledujúci:

Čitateľ je modul zmiešaného súčinu (predstavili sme ho v predchádzajúcej časti) a menovateľ je rovnaký ako v predchádzajúcom vzorci (modul vektorového súčinu smerových vektorov priamych čiar, medzi ktorými je vzdialenosť hľadáme).

To ti pripomeniem

potom vzorec pre vzdialenosť je možné prepísať ako:

Akýsi determinant delený determinantom! Aj keď, pravdu povediac, na vtipy tu nemám čas! Tento vzorec je v skutočnosti veľmi ťažkopádny a vedie k dosť komplikovaným výpočtom. Na tvojom mieste by som to použil len ako poslednú možnosť!

Pokúsme sa vyriešiť niekoľko problémov pomocou vyššie uvedenej metódy:

1. V správnom trojuholníkovom hranole sú všetky hrany rovnaké, nájdite vzdialenosť medzi priamkami a.

2. Vzhľadom na pravotočivý trojuholníkový hranol sú všetky hrany osovej osi roja rovnaké rebrá a re-di-well-rebrá yav-la-et-sya square-ra-tom. Nai di te vzdialenosť medzi priamkou my a

Ja rozhodujem o prvom a na základe neho rozhodujete o druhom!

1. Nakreslite hranol a označte rovné čiary a

Súradnice bodu C: potom

Súradnice bodov

Vektorové súradnice

Súradnice bodov

Vektorové súradnice

Vektorové súradnice

\ [\ left ((B, \ overrightarrow (A (A_1)) \ overrightarrow (B (C_1))) \ right) = \ left | (\ begin (pole) (* (20) (l)) (\ begin (pole) (* (20) (c)) 0 & 1 & 0 \ end (pole)) \\ (\ begin (pole) ( * (20) (c)) 0 & 0 & 1 \ end (pole)) \\ (\ begin (pole) (* (20) (c)) (\ frac ((\ sqrt 3)) (2)) & (- \ frac (1) (2)) & 1 \ end (pole)) \ end (pole)) \ vpravo | = \ frac ((\ sqrt 3)) (2) \]

Uvažujeme o krížovom súbore medzi vektormi a

\ [\ overrightarrow (A (A_1)) \ cdot \ overrightarrow (B (C_1)) = \ left | \ begin (pole) (l) \ begin (pole) (* (20) (c)) (\ overrightarrow i) & (\ overrightarrow j) & (\ overrightarrow k) \ end (array) \\\ begin (pole ) (* (20) (c)) 0 & 0 & 1 \ end (pole) \\\ begin (pole) (* (20) (c)) (\ frac ((\ sqrt 3)) (2)) & (- \ frac (1) (2)) & 1 \ end (pole) \ end (pole) \ vpravo | - \ frac ((\ sqrt 3)) (2) \ overrightarrow k + \ frac (1) (2) \ overrightarrow i \]

Teraz vypočítame jeho dĺžku:

Odpoveď:

Teraz sa pokúste splniť druhú úlohu opatrne. Odpoveď na to bude :.

Súradnice a vektory. Stručný popis a základné vzorce

Vektor je smerovaná úsečka. - začiatok vektora, - koniec vektora.
Vektor je označený alebo.

Absolútna hodnota vektor - dĺžka segmentu predstavujúceho vektor. Je označený ako.

Vektorové súradnice:

,
kde sú konce vektorového \ Displaystyle a.

Súčet vektorov :.

Produkt vektorov:

Bodový súčin vektorov:

Skalárny súčin vektorov sa rovná súčinu ich absolútnych hodnôt kosinusom uhla medzi nimi:

ZOSTÁVAJÚCE 2/3 ČLÁNKY SÚ DOSTUPNÉ LEN PRE ŽIAKOV YOUCLEVER!

Staňte sa študentom YouClever,

Pripravte sa na POUŽITIE alebo VYUŽITIE v matematike za cenu „šálky kávy mesačne“,

A tiež získate neobmedzený prístup k učebnici „YouClever“, školiaciemu programu „100gia“ (reshebnik), neobmedzenému skúšobnému použitiu a OGE, 6000 problémom s analýzou riešení a k ďalším službám YouClever a 100gia.

Nasledujúci článok poukáže na problémy s hľadaním súradníc stredného bodu segmentu, ak ako počiatočné údaje existujú súradnice jeho extrémnych bodov. Ale skôr, ako sa pustíme do skúmania problému, predstavíme niekoľko definícií.

Definícia 1

Čiarový segment- priama čiara spájajúca dva ľubovoľné body, nazývaná konce segmentu. Nech sú to napríklad body A a B a podľa toho segment A B.

Ak segment A B pokračuje v oboch smeroch z bodov A a B, dostaneme priamku A B. Potom je segment A B súčasťou výslednej priamky ohraničenej bodmi A a B. Segment A B spája body A a B, ktoré sú jeho koncami, ako aj množinu bodov ležiacich medzi nimi. Ak napríklad vezmeme ľubovoľný bod K ležiaci medzi bodmi A a B, môžeme povedať, že bod K leží na segmente A B.

Definícia 2

Dĺžka segmentu- vzdialenosť medzi koncami segmentu v danej mierke (segment jednotkovej dĺžky). Dĺžka segmentu A B je označená nasledovne: A B.

Definícia 3

Stred segmentu- bod ležiaci na segmente a v rovnakej vzdialenosti od jeho koncov. Ak je stred segmentu A B označený bodom C, potom rovnosť bude platiť: A C = C B

Počiatočné údaje: súradnicová čiara O x a na nej nesúvisiace body: A a B. Tieto body zodpovedajú reálne čísla x A a x B. Bod C - stredový bod segmentu A B: je potrebné určiť súradnicu x C.

Pretože bod C je stredným bodom segmentu A B, bude platiť nasledujúca rovnosť: | A C | = | C B | ... Vzdialenosť medzi bodmi je určená modulom rozdielu medzi ich súradnicami, t.j.

| A C | = | C B | ⇔ x C - x A = x B - x C

Potom sú možné dve rovnosti: x C - x A = x B - x C a x C - x A = - (x B - x C)

Z prvej rovnosti odvodíme vzorec pre súradnice bodu C: x C = x A + x B 2 (polovica súčtu súradníc koncov segmentu).

Z druhej rovnosti dostaneme: x A = x B, čo je nemožné, pretože v pôvodných údajoch - nesúladné body. Preto vzorec na určenie súradníc stredného bodu segmentu A B s koncami A (x A) a B (x B):

Výsledný vzorec bude základom pre určenie súradníc stredového bodu segmentu v rovine alebo v priestore.

Počiatočné údaje: obdĺžnikový súradnicový systém v rovine O x y, dva ľubovoľné nesúbežné body s danými súradnicami A x A, y A a B x B, y B. Bod C je stredným bodom segmentu A B. Pre bod C je potrebné určiť súradnice x C a y C.

Zoberme si na analýzu prípad, keď sa body A a B nezhodujú a neležia na rovnakej súradnicovej čiare alebo priamke kolmej na jednu z osí. A x, A y; B x, B y a C x, C y - priemety bodov A, B a C na súradnicové osi (priamky O x a O y).

Podľa konštrukcie sú čiary A A x, B B x, C C x rovnobežné; rovné čiary sú tiež navzájom rovnobežné. Spolu s tým podľa Thalesovej vety rovnosť A C = C B znamená rovnosti: A x C x = C x B x a A y C y = C y B y, a tie zase naznačujú, že bod C x je stred segmentu A x B x, a C y je stredový bod segmentu A y B y. A potom, na základe vzorca získaného skôr, dostaneme:

x C = x A + x B 2 a y C = y A + y B 2

Rovnaké vzorce je možné použiť aj v prípade, keď body A a B ležia na tej istej súradnicovej čiare alebo na priamke kolmej na jednu z osí. Podrobnú analýzu tohto prípadu nevykonáme, zvážime ho iba graficky:

Ak zhrnieme všetky vyššie uvedené skutočnosti, súradnice stredového bodu segmentu A B v rovine so súradnicami koncov A (x A, y A) a B (x B, y B) definovaný ako:

(x A + x B 2, y A + y B 2)

Počiatočné údaje: súradnicový systém О x y z a dva ľubovoľné body s danými súradnicami A (x A, y A, z A) a B (x B, y B, z B). Je potrebné určiť súradnice bodu C, ktorý je stredom segmentu A B.

A x, A y, A z; B x, B y, B z a C x, C y, C z - projekcie všetkých uvedených bodov na os súradnicového systému.

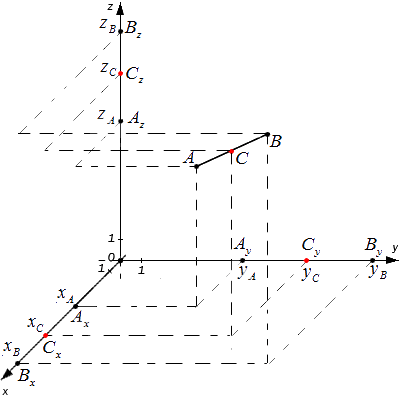
Podľa Thalesovej vety platia nasledujúce rovnosti: A x C x = C x B x, A y C y = C y B y, A z C z = C z B z

Body C x, C y, C z sú teda stredmi segmentov A x B x, A y B y, A z B z, v tomto poradí. Potom, Na určenie súradníc stredového bodu segmentu v priestore platia nasledujúce vzorce:

x C = x A + x B 2, y c = y A + y B 2, z c = z A + Z B 2

Získané vzorce sú použiteľné aj v prípadoch, keď body A a B ležia na jednej zo súradnicových čiar; na priamke kolmej na jednu z osí; v jednej súradnicovej rovine alebo v rovine kolmej na jednu zo súradnicových rovín.

Určenie súradníc stredného bodu segmentu prostredníctvom súradníc vektorov polomeru jeho koncov

Vzorec na nájdenie súradníc stredného bodu segmentu možno odvodiť aj podľa algebraickej interpretácie vektorov.

Počiatočné údaje: pravouhlý karteziánsky súradnicový systém O x y, body s danými súradnicami A (x A, y A) a B (x B, x B). Bod C je stredným bodom segmentu A B.

Podľa geometrickej definície akcií na vektory bude platiť nasledujúca rovnosť: O C → = 1 2 · O A → + O B →. Bod C je v tomto prípade priesečníkom uhlopriečok rovnobežníka zostaveného na základe vektorov O A → a O B →, t.j. stred uhlopriečok. Súradnice vektora polomeru bodu sa rovnajú súradniciam bodu, potom sú rovnosti pravdivé: OA → = (x A, y A), OB → = (x B, y B) . Vykonajme niekoľko operácií s vektormi na súradniciach a získajme:

O C → = 1 2 O A → + O B → = x A + x B 2, y A + y B 2

Bod C má preto súradnice:

x A + x B 2, y A + y B 2

Analogicky je určený vzorec na nájdenie súradníc stredového bodu segmentu v priestore:

C (x A + x B 2, y A + y B 2, z A + z B 2)

Príklady riešenia problémov pri hľadaní súradníc stredového bodu segmentu

Medzi úlohy zahŕňajúce použitie vyššie uvedených vzorcov patria jednak úlohy, v ktorých je priamo zahrnutá otázka výpočtu súradníc stredového bodu segmentu, jednak úlohy, ktoré znamenajú uvedenie daných podmienok na túto otázku: výraz „medián “sa často používa, cieľom je nájsť súradnice jednej z koncov segmentu a tiež bežné problémy so symetriou, ktorých riešenie by vo všeobecnosti nemalo po preštudovaní tejto témy spôsobovať problémy. Uvažujme o typických príkladoch.

Príklad 1

Počiatočné údaje: v rovine - body s danými súradnicami A ( - 7, 3) a B (2, 4). Je potrebné nájsť súradnice stredného bodu segmentu A B.

Riešenie

Označme stred segmentu A B bodom C. Jeho súradnice budú definované ako polovičný súčet súradníc koncov segmentu, t.j. body A a B.

x C = x A + x B 2 = - 7 + 2 2 = - 5 2 y C = y A + y B 2 = 3 + 4 2 = 7 2

Odpoveď: súradnice stredu segmentu A B - 5 2, 7 2.

Príklad 2

Počiatočné údaje: sú známe súradnice trojuholníka A B C: A ( - 1, 0), B (3, 2), C (9, - 8). Je potrebné nájsť dĺžku mediánu A M.

Riešenie

1. Podľa hypotézy problému je M medián, a preto M je stredný bod segmentu B C. V prvom rade nájdeme súradnice stredového bodu segmentu B C, t.j. bod M:

x M = x B + x C 2 = 3 + 9 2 = 6 y M = y B + y C 2 = 2 + ( - 8) 2 = - 3

1. Keďže teraz poznáme súradnice oboch koncov mediánu (body A a M), pomocou vzorca môžeme určiť vzdialenosť medzi bodmi a vypočítať dĺžku mediánu A M:

A M = (6 - ( - 1)) 2 + ( - 3 - 0) 2 = 58

Odpoveď: 58

Príklad 3

Počiatočné údaje: v obdĺžnikovej súradnicovej sústave trojrozmerného priestoru je daný rovnobežnosten A B C D A 1 B 1 C 1 D 1. Sú dané súradnice bodu C 1 (1, 1, 0) a tiež je definovaný bod M, ktorý je stredom uhlopriečky B D 1 a má súradnice M (4, 2, - 4). Je potrebné vypočítať súradnice bodu A.

Riešenie

Uhlopriečky rovnobežnostena majú priesečník v jednom bode, ktorý je stredom všetkých uhlopriečok. Na základe tohto tvrdenia je možné mať na pamäti, že bod M, známy z podmienok problému, je stredovým bodom segmentu A C 1. Na základe vzorca pre hľadanie súradníc stredového bodu segmentu v priestore nájdeme súradnice bodu A: x M = x A + x C 1 2 ⇒ x A = 2 x M - x C 1 = 2 4 - 1 + 7 y M = y A + y C 1 2 ⇒ y A = 2 y M - y C 1 = 2 2 - 1 = 3 z M = z A + z C 1 2 ⇒ z A = 2 z M - z C1 = 2 ( - 4) - 0 = - 8

Odpoveď: súradnice bodu A (7, 3, - 8).

Ak si v texte všimnete chybu, vyberte ju a stlačte kombináciu klávesov Ctrl + Enter

Vektor je veličina charakterizovaná svojou číselnou hodnotou a smerom. Inými slovami, vektor je smerová čiara. Pozícia vektor AB v priestore je daná súradnicami východiskového bodu vektor A a koncové body vektor B. Zvážte, ako určiť súradnice stredu vektor.

Inštrukcie

Najprv definujme označenie začiatku a konca vektor... Ak je vektor zapísaný ako AB, potom bod A je začiatok vektor a bod B je koniec. Naopak, pre vektor BA bod B je začiatok vektor a bod A je koniec. Dostaňme vektor AB so súradnicami pôvodu vektor A = (a1, a2, a3) a koniec vektor B = (bl, b2, b3). Potom súradnice vektor AB bude nasledovné: AB = (b1 - a1, b2 - a2, b3 - a3), t.j. od koncovej súradnice vektor je potrebné odpočítať zodpovedajúcu začiatočnú súradnicu vektor... Dĺžka vektor AB (alebo jeho modul) sa vypočíta ako druhá odmocnina súčtu druhých mocnín jeho súradníc: | AB | =? ((b1 - a1) ^ 2 + (b2 - a2) ^ 2 + (b3 - a3) ^ 2).

Nájdite súradnice bodu, ktorý je v strede vektor... Označme to písmenom O = (o1, o2, o3). Nájdite súradnice stredu vektor rovnako ako súradnice stredu pravidelného segmentu, podľa nasledujúcich vzorcov: o1 = (a1 + b1) / 2, o2 = (a2 + b2) / 2, o3 = (a3 + b3) / 2. Nájdite súradnice vektor AO: AO = (o1 - a1, o2 - a2, o3 - a3) = ((bl - a1) / 2, (b2 - a2) / 2, (b3 - a3) / 2).

Pozrime sa na príklad. Nech je daný vektor AB so súradnicami pôvodu vektor A = (1, 3, 5) a koniec vektor B = (3, 5, 7). Potom súradnice vektor AB možno zapísať ako AB = (3 - 1, 5 - 3, 7 - 5) = (2, 2, 2). Nájdite modul vektor AB: | AB | =? (4 + 4 + 4) = 2 *? 3. Hodnota danej dĺžky vektor nám pomôže ďalej kontrolovať správnosť súradníc stredu vektor... Ďalej nájdeme súradnice bodu O: O = ((1 + 3) / 2, (3 + 5) / 2, (5 + 7) / 2) = (2, 4, 6). Potom súradnice vektor AO sa vypočíta ako AO = (2 - 1, 4 - 3, 6 - 5) = (1, 1, 1).

Skontrolujme to. Dĺžka vektor AO =? (1 + 1 + 1) = -3. Pripomeňme, že dĺžka iniciály vektor sa rovná 2 *? 3, t.j. polovicu vektor sa skutočne rovná polovici dĺžky originálu vektor... Teraz vypočítajme súradnice vektor OB: OB = (3 - 2, 5 - 4, 7 - 6) = (1, 1, 1). Nájdite súčet vektorov AO a OB: AO + OB = (1 + 1, 1 + 1, 1 + 1) = (2, 2, 2) = AB. Preto súradnice stredu vektor boli nájdené správne.

Užitočné rady

Po výpočte súradníc stredu vektora určite vykonajte aspoň najjednoduchšiu kontrolu - vypočítajte dĺžku vektora a porovnajte ho s dĺžkou daného vektora.

Nakoniec sa mi do rúk dostala rozsiahla a dlho očakávaná téma analytická geometria... Najprv trochu o tejto časti vyššej matematiky ... Iste vám teraz pripomína školský kurz geometrie s početnými vetami, ich dôkazmi, kresbami atď. Čo skrývať, nemilovaný a často nejasný predmet pre značnú časť študentov. Analytická geometria sa napodiv môže zdať zaujímavejšia a prístupnejšia. Čo znamená prídavné meno analytický? Hneď sa mi vybavia dve opečiatkované matematické odbočky: „metóda grafického riešenia“ a „metóda analytického riešenia“. Grafická metóda, samozrejme, je spojená s konštrukciou grafov, kresieb. Analytické rovnaký metóda zahŕňa riešenie problémov prevažne prostredníctvom algebraických akcií. V tomto ohľade je algoritmus na riešenie takmer všetkých problémov analytickej geometrie jednoduchý a transparentný, často stačí starostlivo použiť potrebné vzorce - a odpoveď je pripravená! Nie, samozrejme, nezaobíde sa to vôbec bez kresieb, okrem toho sa ich pre lepšie pochopenie materiálu pokúsim citovať nad nevyhnutnosť.

Otvorený kurz hodín geometrie sa netvári ako teoretická úplnosť, je zameraný na riešenie praktických problémov. Do svojich prednášok zaradím len to, čo je z môjho pohľadu dôležité z praktického hľadiska. Ak potrebujete komplexnejšiu pomoc v ktoromkoľvek pododdiele, odporúčam vám nasledujúcu ľahko dostupnú literatúru:

1) Vec, s ktorou je vtip, je známe niekoľko generácií: Učebnica školskej geometrie, autori - L.S. Atanasyan a spoločnosť... Tento vešiak školskej šatne už vydržal 20 (!) Dotlačí, čo však samozrejme nie je limit.

2) Geometria v 2 zväzkoch... Autori L.S. Atanasyan, Bazylev V.T.... Toto je literatúra pre stredná škola potrebuješ prvý zväzok... Vzácne úlohy mi môžu vypadnúť z očí, a návod poskytne neoceniteľnú pomoc.

Obe knihy je možné zadarmo stiahnuť na internete. Navyše môj archív môžete použiť s hotovými riešeniami, ktoré nájdete na stránke Stiahnite si príklady z vyššej matematiky.

Zo súboru nástrojov opäť navrhujem svoj vlastný vývoj - softvérový balík o analytickej geometrii, čo výrazne zjednoduší život a ušetrí veľa času.

Predpokladá sa, že čitateľ je oboznámený so základným geometrické koncepty a tvary: bod, čiara, rovina, trojuholník, rovnobežník, rovnobežnosten, kocka atď. Odporúča sa pamätať na niektoré vety, aspoň na Pytagorovu vetu, ahoj opakovačom)

A teraz budeme postupne zvažovať: koncept vektora, akcie s vektormi, súradnice vektora. Ďalej odporúčam prečítať zásadný článok Bodový súčin vektorov a tiež Vektor a zmiešaný súčin vektorov... Nadbytočná nebude ani miestna úloha - Rozdelenie segmentu v tomto ohľade. Na základe vyššie uvedených informácií môžete ovládať rovnica priamky v rovine s najjednoduchšie príklady riešeníčo umožní Naučte sa riešiť problémy v geometrii... Nasledujúce články sú tiež nápomocné: Rovnica roviny v priestore, Rovnice priamky v priestore, Základné úlohy na priamke a rovine, ďalšie sekcie analytickej geometrie. Prirodzene, počas cesty sa budú brať do úvahy štandardné úlohy.

Vektorové koncept. Voľný vektor

Najprv si zopakujme školskú definíciu vektora. Vektor zavolal režírovaný segment, pre ktorý je uvedený jeho začiatok a koniec:

V tomto prípade je začiatok segmentu bod, koniec segmentu je bod. Samotný vektor je označený symbolom. Smer je nevyhnutné, ak zmeníte usporiadanie šípky na druhý koniec segmentu, dostanete vektor a toto už je úplne iný vektor... Je vhodné stotožniť koncept vektora s pohybom fyzického tela: musíte súhlasiť, vstup do dverí ústavu alebo opustenie dverí ústavu sú úplne odlišné veci.

Je vhodné považovať jednotlivé body roviny, priestoru za tzv nulový vektor... Takýto vektor má rovnaký koniec a začiatok.

!!! Poznámka: Ďalej môžete predpokladať, že vektory ležia v rovnakej rovine, alebo môžete predpokladať, že sa nachádzajú v priestore - podstata predloženého materiálu platí pre rovinu aj pre priestor.

Legenda: Mnohí si okamžite všimli prútik bez šípky v označení a povedali, na tom istom mieste dali šíp hore! Je pravda, že môžete písať šípkou :, ale je to tiež možné záznam, ktorý použijem v budúcnosti... Prečo? Tento zvyk sa zrejme vyvinul z praktických úvah, moji strelci sa v škole a na univerzite ukázali ako príliš rozmanití a huňatí. Vo vzdelávacej literatúre sa niekedy vôbec neobťažujú s klinovým písmom, ale zvýrazňujú písmená tučným písmom :, čím naznačujú, že ide o vektor.

To bol štýl, ale teraz o spôsoboch písania vektorov:

1) Vektory môžu byť napísané dvoma veľkými latinskými písmenami:
atď. V tomto prípade prvé písmeno nevyhnutne označuje počiatočný bod vektora a druhé písmeno označuje koncový bod vektora.

2) Vektory sú tiež napísané malými latinskými písmenami:
Najmä náš vektor môže byť pre krátkosť označený malým latinským písmenom.

Dĺžka alebo modul nenulový vektor je dĺžka segmentu. Dĺžka nulového vektora je nula. Je to logické.

Dĺžka vektora je označená znamienkom modulu :,

O tom, ako zistiť dĺžku vektora, sa naučíme (alebo zopakujeme, pre koho ako) o niečo neskôr.

Toto boli základné informácie o vektore, známe všetkým školákom. V analytickej geometrii tzv voľný vektor.

Ak je to celkom jednoduché - vektor je možné odložiť z akéhokoľvek bodu:

Kedysi sme takéto vektory nazývali rovnakými (definícia rovnakých vektorov bude uvedená nižšie), ale z čisto matematického hľadiska je to JEDEN A ROVNAKÝ VEKTOR resp. voľný vektor... Prečo zadarmo? Pretože v priebehu riešenia problémov môžete „pripevniť“ ten alebo onen „školský“ vektor k akémukoľvek bodu lietadla alebo priestoru, ktorý potrebujete. Toto je veľmi cool nehnuteľnosť! Predstavte si smerovaný segment ľubovoľnej dĺžky a smeru - dá sa „klonovať“ nekonečne veľakrát a v každom bode priestoru, v skutočnosti existuje KAŽDÝ. Jeden študent hovorí: Každý prednášajúci vo f ** k a vektore. Koniec koncov, nielen vtipná riekanka, všetko je takmer správne - môže tam byť pridaný aj riadený segment. Neponáhľajte sa však radovať, študenti sami častejšie trpia =)

Takže, voľný vektor- Toto kopa identické nasmerované segmenty. Školská definícia vektora uvedená na začiatku odseku: „Vektor sa nazýva smerovaný segment ...“ znamená, že špecifické smerovaný segment odobratý z danej množiny, ktorý je viazaný na konkrétny bod v rovine alebo priestore.

Je potrebné poznamenať, že z hľadiska fyziky je koncept voľného vektora spravidla nesprávny a záleží na bode aplikácie. Skutočne, priamy úder rovnakou silou na nos alebo na čelo bude stačiť na to, aby sa vyvinul môj hlúpy príklad, ktorý má rôzne dôsledky. Avšak, nie zadarmo vektory sa nachádzajú aj v priebehu strednej školy (nechoďte tam :)).

Akcie s vektormi. Kolineárne vektory

IN školský kurz geometria, zvažuje sa niekoľko akcií a pravidiel s vektormi: sčítanie podľa pravidla trojuholníka, sčítanie podľa pravidla rovnobežníka, pravidlo vektorového rozdielu, násobenie vektora číslom, skalárny súčin vektorov atď. Pre osivo zopakujeme dve pravidlá, ktoré sú obzvlášť dôležité pre riešenie problémov analytickej geometrie.

Pravidlo sčítania vektorov podľa pravidla trojuholníkov

Zvážte dva ľubovoľné nenulové vektory a:

Je potrebné nájsť súčet týchto vektorov. Pretože všetky vektory sú považované za voľné, vektor sme vyčlenili z koniec vektory:

Súčet vektorov je vektor. Pre lepšie pochopenie pravidla je vhodné vložiť do neho fyzický význam: nech nejaké telo urobí cestu pozdĺž vektora a potom pozdĺž vektora. Potom je súčet vektorov vektorom výslednej cesty so začiatkom v mieste odchodu a koncom v mieste príchodu. Podobné pravidlo je formulované pre súčet ľubovoľného počtu vektorov. Ako sa hovorí, telo sa môže silne pohybovať po cikcaku a možno aj na autopilote - podľa výsledného vektora súčtu.

Mimochodom, ak vektor odložíme z začať vektor, dostanete ekvivalent pravidlo rovnobežníka pridanie vektorov.

Po prvé, o kolinearite vektorov. Tieto dva vektory sa nazývajú kolineárne ak ležia na tej istej čiare alebo na rovnobežných čiarach. Zhruba povedané, hovoríme o paralelných vektoroch. Ale vo vzťahu k nim sa vždy používa prídavné meno „kolineárne“.

Predstavte si dva kolineárne vektory. Ak sú šípky týchto vektorov nasmerované rovnakým smerom, potom sa takéto vektory nazývajú spolurežírovaný... Ak šípky ukazujú v rôznych smeroch, potom budú vektory opačný smer.

Legenda: kolinearita vektorov je zapísaná zvyčajným symbolom rovnobežnosti :, pričom detaily sú možné: (vektory sú smerované spoločne) alebo (vektory sú nasmerované opačne).

Podľa produktu nenulový vektor podľa čísla je taký vektor, ktorého dĺžka je rovnaká, a vektory a sú vedené spoločne a opačne.

Pravidlo vynásobenia vektora číslom je jednoduchšie pochopiť pomocou obrázku:

Poďme pochopiť podrobnejšie:

1) Smer. Ak je faktor záporný, potom vektor mení smer na opak.

2) Dĺžka. Ak je faktor vnútri alebo, potom je dĺžka vektora klesá... Dĺžka vektora je teda polovica dĺžky vektora. Ak je modul väčší ako jeden, potom dĺžka vektora zvyšuje na čas.

3) Upozorňujeme, že všetky vektory sú kolineárne, zatiaľ čo jeden vektor je vyjadrený napríklad v inom. Opak je tiež pravdivý: ak jeden vektor môže byť vyjadrený inými, potom sú tieto vektory nevyhnutne kolineárne. Preto: ak vynásobíme vektor číslom, dostaneme kolineár(vo vzťahu k originálu) vektor.

4) Vektory sú jednosmerné. Vektory a sú tiež jednosmerné. Akýkoľvek vektor z prvej skupiny je opačne nasmerovaný vzhľadom na akýkoľvek vektor z druhej skupiny.

Ktoré vektory sú rovnaké?

Dva vektory sú rovnaké, ak sú jednosmerné a majú rovnakú dĺžku... Všimnite si toho, že smerovosť znamená kolineárne vektory. Definícia bude nepresná (nadbytočná), ak povieme: „Dva vektory sú rovnaké, ak sú kolineárne, jednosmerné a majú rovnakú dĺžku.“

Z hľadiska koncepcie voľného vektora sú rovnaké vektory jedným a tým istým vektorom, o ktorom sa už diskutovalo v predchádzajúcom odseku.

Vektorové súradnice v rovine a vo vesmíre

Prvým bodom je zvážiť vektory v rovine. Reprezentujeme karteziánsky obdĺžnikový súradnicový systém a vyčnievame od začiatku súradníc slobodný vektory a:

Vektory a ortogonálne... Ortogonálne = kolmé. Odporúčam si pomaly zvyknúť na pojmy: namiesto rovnobežnosti a kolmosti používame slová, resp kolinearita a ortogonalita.

Označenie: ortogonalita vektorov sa zapisuje zvyčajným symbolom kolmosti, napríklad :.

Uvažované vektory sa nazývajú súradnicové vektory alebo orty... Tieto vektory sa tvoria základ na povrchu. Čo je podľa mňa základ, je mnohým intuitívne jasné detailné informácie nájdete v článku Lineárna (ne) závislosť vektorov. Základ vektorov Jednoducho povedané, základ a pôvod súradníc definujú celý systém - je to druh základu, na ktorom je plný a bohatý geometrický život v plnom prúde.

Niekedy sa nazýva konštruovaný základ ortonormálne základ roviny: „orto“ - pretože súradnicové vektory sú ortogonálne, prídavné meno „normalizovaný“ znamená jednotku, t.j. dĺžky vektorov základu sú rovné jednej.

Označenie: základ je spravidla napísaný v zátvorkách, vo vnútri ktorých v prísnom poradí sú uvedené základné vektory, napríklad :. Súradnicové vektory je zakázané preskupiť.

akýkoľvek vektorové lietadlo jedinečný spôsob vyjadrené ako:
, kde - čísla ktorým sa hovorí vektorové súradnice na tomto základe. A samotný výraz zavolal rozklad vektorana základe .

Večera sa podáva:

Začnime prvým písmenom abecedy :. Výkres jasne ukazuje, že pri rozširovaní vektora z hľadiska základu sa používajú práve uvažované:
1) pravidlo pre vynásobenie vektora číslom: a;
2) pridanie vektorov podľa pravidla trojuholníka :.

Teraz mentálne odložte vektor z akéhokoľvek iného bodu v rovine. Je úplne zrejmé, že jeho rozklad „ho bude nemilosrdne nasledovať“. Tu je sloboda vektora - vektora „nesie všetko so sebou“. Táto vlastnosť samozrejme platí pre akýkoľvek vektor. Je zábavné, že samotné základné (bezplatné) vektory nemusia byť odložené od začiatku, jeden môže byť nakreslený napríklad vľavo dole a druhý vpravo hore a nič sa na tom nezmení! Je pravda, že to nemusíte robiť, pretože učiteľ tiež ukáže originalitu a nakreslí vás „pripísaných“ na nečakané miesto.

Vektory ilustrujú presne pravidlo násobenia vektora číslom, vektor je jednosmerný so základným vektorom, vektor je oproti základnému vektoru. Tieto vektory majú jednu zo súradníc rovnú nule, je možné ich starostlivo zapísať takto:


A základné vektory, mimochodom, takto: (v skutočnosti sú vyjadrené samy).

A nakoniec:,. Mimochodom, čo je to vektorové odčítanie a prečo som nehovoril o pravidle odčítania? Niekde v lineárnej algebre si nepamätám kde, poznamenal som, že odčítanie je špeciálny prípad sčítania. Rozšírenia vektorov „de“ a „e“ sú teda ticho zapísané ako súčet :, ... Nasledujte výkres, ako v týchto situáciách funguje dobre starý dobrý trojuholník vektorov.

Uvažovaný rozklad formy niekedy sa nazýva vektorový rozklad v systéme ort(t.j. v sústave jednotkových vektorov). Nie je to však jediný spôsob, ako napísať vektor, je bežná nasledujúca možnosť:

Alebo so znamienkom rovnosti:

Samotné základné vektory sú zapísané nasledovne: a

To znamená, že súradnice vektora sú uvedené v zátvorkách. V praktických úlohách sú použité všetky tri možnosti záznamu.

Pochyboval som, či mám hovoriť, ale napriek tomu poviem: súradnice vektorov nemožno usporiadať. Prísne na prvom mieste napíšte súradnicu, ktorá zodpovedá jednotkovému vektoru, prísne na druhom mieste napíšte súradnicu, ktorá zodpovedá jednotkovému vektoru. Skutočne sú to dva rôzne vektory.

Zistili sme súradnice v lietadle. Teraz sa pozrime na vektory v 3D priestore, tu je to takmer rovnaké! Bude pridaná iba jedna ďalšia súradnica. Je ťažké vykonávať trojrozmerné kresby, takže sa obmedzím na jeden vektor, ktorý kvôli jednoduchosti odložím od pôvodu:

akýkoľvek vektor trojrozmerného priestoru môže jediná cesta rozbaliť v ortonormálnom základe:
, kde sú súradnice vektora (čísla) v danom základe.

Príklad z obrázku: ... Pozrime sa, ako tu fungujú vektorové pravidlá. Najprv vynásobte vektor číslom: (červená šípka), (zelená šípka) a (karmínová šípka). Za druhé, tu je príklad pridania niekoľkých, v tomto prípade troch vektorov :. Súčetový vektor začína v počiatočnom bode odchodu (vektorový začiatok) a spočíva v konečnom bode príchodu (koncový vektor).

Všetky vektory trojrozmerného priestoru sú, samozrejme, tiež voľné, skúste vektor mentálne odložiť z akéhokoľvek iného bodu a pochopíte, že jeho rozklad „zostane s ním“.

Podobne ako ploché puzdro, okrem písania široko sa používajú verzie so zátvorkami: buď.

Ak jeden (alebo dva) súradnicové vektory v expanzii chýbajú, potom sú na ich miesto vložené nuly. Príklady:
vektor (starostlivo ) - zapíšte si;
vektor (starostlivo ) - zapíšte si;
vektor (starostlivo ) - zapíšeme si to.

Základné vektory sú zapísané nasledovne:

Tu sú snáď všetky minimálne teoretické znalosti potrebné na riešenie problémov v analytickej geometrii. Možno existuje príliš veľa pojmov a definícií, preto odporúčam figurínam, aby si tieto informácie znova prečítali a porozumeli im. A bude užitočné, aby sa každý čitateľ čas od času obrátil na základnú lekciu kvôli lepšej asimilácii materiálu. Kolinearita, ortogonalita, ortonormálny základ, vektorový rozklad - tieto a ďalšie koncepty budú často použité v nasledujúcom texte. Poznamenávam, že materiály na webe nestačia na absolvovanie teoretického testu, kolokvia o geometrii, pretože všetky vety starostlivo šifrujem (okrem toho bez dôkazov) - na úkor vedeckého štýlu prezentácie, ale plus pre vaše chápanie predmetu. Aby som získal podrobné teoretické znalosti, žiadam vás, aby ste sa uklonili pred profesorom Atanasyanom.

A prejdeme k praktickej časti:

Najjednoduchšie problémy analytickej geometrie.
Akcie s vektormi v súradniciach

Je veľmi žiaduce naučiť sa riešiť úlohy, ktoré budú zvažované na plnom stroji, a vzorce zapamätať si, dokonca ani špeciálne memorovanie, budú si ich pamätať =) To je veľmi dôležité, pretože ostatné problémy analytickej geometrie sú založené na najjednoduchších elementárnych príkladoch a bude nepríjemné tráviť viac času jedením pešiakov. Nie je potrebné zapínať horné gombíky na tričku, veľa vecí je vám známych zo školy.

Prezentácia materiálu bude prebiehať súbežne - pre lietadlo aj pre priestor. Z toho dôvodu, že všetky vzorce ... uvidíte sami.

Ako nájsť vektor podľa dvoch bodov?

Ak sú zadané dva body roviny, vektor má nasledujúce súradnice:

Ak sú zadané dva body priestoru, vektor má nasledujúce súradnice:

Tj. zo súradníc konca vektora musíte odpočítať zodpovedajúce súradnice začiatok vektora.

Úloha: Pre rovnaké body napíšte vzorce na nájdenie súradníc vektora. Vzorce na konci hodiny.

Príklad 1

Dva body roviny a sú dané. Nájdite vektorové súradnice

Riešenie: podľa zodpovedajúceho vzorca:

Alternatívne je možné použiť nasledujúci záznam:

Estetici sa rozhodnú takto:

Osobne som zvyknutý na prvú verziu záznamu.

Odpoveď:

Podľa podmienky nebolo potrebné zostaviť výkres (čo je typické pre úlohy analytickej geometrie), ale aby som figurínam vysvetlil niektoré body, nebudem príliš lenivý:

Je nevyhnutné porozumieť rozdiel medzi súradnicami bodov a vektorovými súradnicami:

Súradnice bodov Sú obvyklé súradnice v obdĺžnikovom súradnicovom systéme. Myslím, že každý vie, ako položiť body na súradnicovej rovine už od 5.-6. ročníka. Každý bod má v lietadle svoje prísne miesto a nemôžete ho nikam posúvať.

Súradnice vektora V tomto prípade ide o jeho rozšírenie. Akýkoľvek vektor je bezplatný, preto ak je to žiaduce alebo nevyhnutné, môžeme ho ľahko odložiť z iného bodu roviny (aby sme sa vyhli zmätkom, napríklad jeho premenovaním na). Je zaujímavé, že pre vektory nie je možné vôbec stavať osi, pravouhlý súradnicový systém, stačí iba základ, v tomto prípade ortonormálny základ roviny.

Záznamy súradníc bodov a súradníc vektorov sa zdajú byť podobné :, a význam súradníc absolútne rôzne a tento rozdiel by ste si mali dobre uvedomiť. Tento rozdiel, samozrejme, platí aj pre priestor.

Dámy a páni, plníme si ruky:

Príklad 2

a) Body a sú dané. Nájdite vektory a.
b) Body sú dané a. Nájdite vektory a.
c) Body a sú dané. Nájdite vektory a.
d) Body sú dané. Nájdite vektory .

Dosť, snáď. Toto sú príklady nezávislého riešenia, snažte sa ich nezanedbávať, vyplatí sa to ;-). Nie je potrebné vytvárať kresby. Riešenia a odpovede na konci hodiny.

Čo je dôležité pri riešení problémov v analytickej geometrii? Je dôležité byť EXTRÉMNE OPATRNÝ, aby ste sa vyhli chybe z workshopu „dva plus dva sa rovná nule“. Hneď sa ospravedlňujem, ak som niekde urobil chybu =)

Ako zistím dĺžku úsečky?

Dĺžka, ako už bolo uvedené, je označená znakom modulu.

Ak sú dané dva body roviny a sú dané, potom je možné dĺžku segmentu vypočítať podľa vzorca

Ak sú dané dva body priestoru a sú dané, potom dĺžku segmentu možno vypočítať podľa vzorca

Poznámka: Vzorce zostanú správne, ak sú zodpovedajúce súradnice preusporiadané: a, ale prvá možnosť je štandardnejšia

Príklad 3

Riešenie: podľa zodpovedajúceho vzorca:

Odpoveď:

Pre prehľadnosť urobím kresbu

Čiarový segment - toto nie je vektor, a samozrejme to nemôžete nikam presunúť. Okrem toho, ak dokončíte výkres v mierke: 1 jednotka. = 1 cm (dve bunky prenosného počítača), potom je možné získanú odpoveď skontrolovať bežným pravítkom, pričom sa priamo meria dĺžka segmentu.

Áno, riešenie je krátke, ale existuje niekoľko ďalších dôležité body, ktoré by som chcel objasniť:

Najprv v odpovedi uvádzame dimenziu: „jednotky“. Podmienka nehovorí ČO to je, milimetre, centimetre, metre alebo kilometre. Matematicky správnym riešením by preto bola všeobecná formulácia: „jednotky“ - skrátene ako „jednotka“.

Za druhé, zopakujme si to školský materiál, čo je užitočné nielen pre zvažovanú úlohu:

dávaj pozor na dôležitá technika – vytiahnutie faktora spod koreňa... Výsledkom výpočtov je výsledok a dobrý matematický štýl zahŕňa vybratie faktora spod koreňa (ak je to možné). Podrobnejšie tento proces vyzerá takto: ... Ponechanie odpovede vo formulári samozrejme nebude chybou - ale určite chybou a závažným argumentom pre otravovanie učiteľa.

Ďalšími bežnými prípadmi sú:

Pod koreňom sa napríklad často získa dosť veľký počet. Čo robiť v takýchto prípadoch? Na kalkulačke skontrolujte, či je číslo deliteľné 4 :. Áno, bolo to úplne rozdelené, takže: ... Alebo možno možno číslo opäť rozdeliť na 4? ... Preto: ... Posledná číslica čísla je nepárna, takže zjavne nie je možné tretíkrát deliť 4. Pokúšame sa rozdeliť na deväť :. Ako výsledok:
Pripravený.

Záver: ak sa pod koreňom získa neextrahovateľné číslo, potom sa pokúsime odstrániť multiplikátor spod koreňa - na kalkulačke skontrolujeme, či je číslo deliteľné: 4, 9, 16, 25, 36, 49 atď.

Pri riešení rôznych problémov sa často stretávame s koreňmi, vždy sa snažte extrahovať faktory spod koreňa, aby ste sa vyhli nižšej známke a zbytočným problémom s upresňovaním vašich riešení podľa poznámky učiteľa.

Zopakujme si rovnanie a ostatné mocniny súčasne:

Pravidlá pre zvládnutie diplomov vo všeobecnosti nájdete v školskej učebnici algebry, ale myslím si, že z uvedených príkladov je už všetko alebo takmer všetko jasné.

Úloha pre nezávislé riešenie so segmentom v priestore:

Príklad 4

Body a sú dané. Nájdite dĺžku úsečky.

Riešenie a odpoveď na konci hodiny.

Ako zistím dĺžku vektora?

Ak je daný rovinný vektor, jeho dĺžka sa vypočíta podľa vzorca.

Ak je daný vektor priestoru, jeho dĺžka sa vypočíta podľa vzorca .

Tieto vzorce (ako aj vzorce pre dĺžku segmentu) možno ľahko odvodiť pomocou známej Pytagorovej vety.