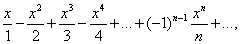
lukhov Yu.P. Prednášky o vyššej matematike. Prednáška číslo 42 5

Prednáška 42

TÉMA: Funkčné hodnosti

Plán.

1. Funkčné riadky. Konvergenčný región.
2. Rovnomerná konvergencia. Značka Weierstrass.
3. Vlastnosti rovnomerne konvergujúcich radov: spojitosť súčtu radu, integrácia a diferenciácia z hľadiska termínov.
4. Silová séria. Ábelova veta. Konvergenčná oblasť výkonových radov. Polomer konvergencie.
5. Základné vlastnosti mocninových radov: rovnomerná konvergencia, spojitosť a nekonečná diferenciácia súčtu. Časovo integrovaná integrácia a diferenciácia výkonových radov.

Funkčné riadky. Konvergenčný región

Definícia 40.1. Nekonečný súčet funkcií

u 1 (x) + u 2 (x) +… + u n (x) +…, (40,1)

kde sa volá u n (x) = f (x, n) funkčný rozsah.

Ak nastavíte konkrétnu číselnú hodnotu NS , séria (40.1) sa zmení na číselnú sériu a v závislosti od výberu hodnoty NS taká séria sa môže zbiehať alebo rozchádzať. Praktické hodnoty majú iba konvergujúce série, preto je dôležité tieto hodnoty určiť NS , pri ktorej sa funkčný rad stáva konvergujúcim číselným radom.

Definícia 40.2. Mnoho významov NS , keď sa nahradí do funkčného radu (40.1), získa sa konvergujúci numerický rad, sa nazývakonvergenčná doménafunkčný rozsah.

Definícia 40.3. Funkcia s (x), definované v oblasti konvergencie radu, ktorá pre každú hodnotu NS z oblasti konvergencie sa rovná súčtu zodpovedajúcich číselných radov získaných z (40.1) pre danú hodnotu x sa nazýva súčet funkčných radov.

Príklad. Nájdite oblasť konvergencie a súčet funkčných radov

1 + x + x ² + ... + x n + ...

Kedy | X | ≥ 1, preto sa zodpovedajúce číselné rady líšia. Ak

| X | < 1, рассматриваемый ряд представляет собой сумму бесконечно убывающей геометрической прогрессии, вычисляемую по формуле:

V dôsledku toho je rozsahom konvergencie radu interval (-1, 1) a jeho súčet má uvedenú formu.

Komentovať ... Rovnako ako pre číselné rady, môžete zaviesť koncept čiastočného súčtu funkčného radu:

s n = 1 + x + x ² + ... + x n

a zvyšok riadka: r n = s - s n.

Rovnomerná konvergencia funkčného radu

Najprv definujme koncept rovnomernej konvergencie číselnej postupnosti.

Definícia 40.4. Funkčná postupnosť f n (x) sa nazýva rovnomerne konvergujúce k funkcii f na súprave X, ak a

Poznámka 1. Označíme obvyklú konvergenciu funkčnej postupnosti a rovnomernú konvergenciu -.

Poznámka 2 ... Znovu zaznamenávame zásadný rozdiel medzi rovnomernou konvergenciou a bežnou konvergenciou: v prípade bežnej konvergencie pre zvolenú hodnotu ε pre každú existuje tvoje číslo N, pre ktoré o n> N. nerovnosť platí:

V takom prípade sa môže ukázať, že pre dané ε zvoľte spoločné číslo N, zabezpečenie splnenia tejto nerovnosti pre kohokoľvek NS , nemožné. V prípade rovnomernej konvergencie také číslo N spoločných pre všetky x existuje.

Teraz definujme koncept rovnomernej konvergencie funkčného radu. Pretože každá séria zodpovedá sekvencii jej čiastkových súčtov, rovnomerná konvergencia radu je určená rovnomernou konvergenciou tejto postupnosti:

Definícia 40.5. Funkčný rozsah sa nazývarovnomerne konvergujúce na súprave X, ak na X postupnosť jeho čiastkových súčtov sa zbieha jednotne.

Značka Weierstrass

Veta 40.1. Ak sa číselný rad zbieha pre všetkých a pre všetkých n = 1, 2, ... nerovnosť platí, potom sa séria absolútne a jednotne zbieha na množine NS.

Dôkaz.

Pre akékoľvek ε> 0 c existuje také číslo N, preto

Pre zvyšky r n niekoľko spravodlivých odhadov

Séria sa preto zbieha jednotne.

Komentovať. Obvykle sa nazýva postup výberu číselných radov spĺňajúcich podmienky vety 40.1 majorizácia , a samotný tento riadok - majorant pre daný funkčný rozsah.

Príklad. Pre funkčnú sériu majorant pre každú hodnotu NS je zbližujúca sa pozitívna séria. Pôvodná séria preto konverguje rovnomerne na (-∞, + ∞).

Vlastnosti rovnomerne konvergujúcich radov

Veta 40.2. Ak funkcie u n (x) sú spojité pre a séria sa rovnomerne zbieha ďalej X, potom jeho súčet s (x) je tiež v bode súvislý x 0.

Dôkaz.

Vyberieme ε> 0. Potom potom existuje také číslo n 0 to

- súčet konečného počtu spojitých funkcií, pretospojité v bode x 0. Preto existuje δ> 0 také, že Potom dostaneme:

To znamená, že funkcia s (x) je spojitá pri x = x 0.

Veta 40.3. Nech funkcie u n (x) sú spojité v segmente [ a, b ] a séria sa v tomto segmente rovnomerne zbieha. Potom sa séria tiež rovnomerne zbieha na [ a, b] a (40.2)

(to znamená, že za podmienok vety môže byť séria časovo integrovaná).

Dôkaz.

Podľa vety 40.2, funkcia s (x) = je spojité na [a, b ], a preto je na ňom integrovateľný, to znamená, že integrál na ľavej strane rovnosti (40.2) existuje. Ukážme, že séria konverguje k funkcii rovnomerne

Označujeme

Potom pre akékoľvek ε existuje číslo N, ktoré pre n> N

Séria teda konverguje rovnomerne a jej súčet sa rovná σ ( x) =.

Veta je dokázaná.

Veta 40.4. Nech funkcie u n (x) kontinuálne diferencovateľné v segmente [ a, b ] a rad zložený z ich derivátov:

(40.3)

rovnomerne konverguje na [ a, b ]. Potom, ak sa séria zbližuje aspoň v jednom bode, potom sa zbieha rovnomerne v celom [ a, b], jeho súčet s (x) = je kontinuálne diferencovateľnou funkciou a

(sériu je možné diferencovať podľa termínu).

Dôkaz.

Definujeme funkciu σ ( NS ) ako. Podľa vety 40.3 možno sériu (40,3) integrovať priebežne:

Séria na pravej strane tejto rovnosti sa rovnomerne zbieha na [ a, b ] od vety 40.3. Číselný rad sa však zbližuje s hypotézou vety, preto sa rad tiež konverguje jednotne. Potom funkcia σ ( t ) je súčet rovnomerne konvergentných sérií spojitých funkcií na [ a, b ], a preto je sám súvislý. Potom je funkcia plynule diferencovateľná na [ a, b ] a podľa potreby.

Definícia 41.1. Silová séria sa nazýva funkčná séria formulára

(41.1)

Komentovať. Nahradením x - x 0 = t radu (41.1) je možné redukovať na tvar; preto stačí dokázať všetky vlastnosti mocninových radov pre série tvaru

(41.2)

Veta 41,1 (Ábelova 1. veta).Ak sa výkonová rada (41.2) zbieha pre x = x 0, potom pre akékoľvek x: | x |< | x 0 | séria (41.2) absolútne konverguje. Ak sa séria (41.2) rozchádza o x = x 0, potom sa to líši pre každého x: | x | > | x 0 |.

Dôkaz.

Ak sa séria zbieha, existuje teda konštanta c> 0:

V dôsledku toho je séria pre | x |<| x 0 | konverguje, pretože je to súčet nekonečne sa znižujúcej geometrickej postupnosti. Preto je séria pre | x |<| x 0 | absolútne konverguje.

Ak je známe, že séria (41.2) sa líši pre x = x 0 , potom nemôže konvergovať pre | x | > | x 0 | , pretože z toho, čo bolo predtým dokázané, bude vyplývať, že sa to tiež v bode zbieha x 0.

Ak teda nájdeme najväčšie z čísel x 0 > 0 také, že (41.2) konverguje pre x = x 0, potom doménou konvergencie tejto série, ako vyplýva z Ábelovej vety, bude interval (- x 0, x 0 ), prípadne vrátane jednej alebo oboch hraníc.

Definícia 41.2. Zavolá sa číslo R ≥ 0 polomer konvergencievýkonový rad (41.2), ak tento rad konverguje, ale líši sa. Interval (- R, R) sa nazýva konvergenčný interval séria (41,2).

Príklady.

1. Na štúdium absolútnej konvergencie série používame d'Alembertovo kritérium:. V dôsledku toho sa séria zbieha iba pre NS = 0 a polomer jeho konvergencie je 0: R = 0.
2. Použitím rovnakého d'Alembertovho testu je možné preukázať, že séria konverguje pre ľubovoľnú x, to je
3. Pre sériu založenú na d'Alemberte získame:

Preto v čase –1< X < 1 ряд сходится, при

X< -1 и x > 1 sa líši. O NS = 1 získame harmonický rad, ktorý, ako je známe, sa líši a pre NS = -1 séria konvenčne konverguje na základe Leibnizova. Polomer konvergencie uvažovaného radu je teda R. = 1 a konvergenčný interval je [-1, 1).

Vzorce na stanovenie polomeru konvergencie výkonovej rady.

1. D'Alembertov vzorec.

Zvážte mocninovú sériu a použite na ňu d'Alembertov test: na to, aby sa série zbiehali, je potrebné, aby. Ak existuje, potom je oblasť konvergencie určená nerovnosťou, tj.

- (41.3)

• d'Alembertov vzorecna výpočet polomeru konvergencie.

1. Cauchyho-Hadamardov vzorec.

Použitím radikálneho Cauchyovho kritéria a argumentovaním podobným spôsobom zistíme, že môžeme definovať doménu konvergencie mocninovej série ako súbor riešení nerovnosti za predpokladu, že existuje táto hranica, a podľa toho nájsť iný vzorec pre polomer konvergencie. :

(41.4)

• Cauchyho-Hadamardov vzorec.

Vlastnosti výkonových radov.

Veta 41,2 (Ábelova 2. veta). Ak R. Je polomer konvergencie radu (41.2) a tento rad konverguje na x = R. , potom sa rovnomerne zbieha v intervale (- R, R).

Dôkaz.

Pozitívna séria konverguje podľa vety 41.1. V dôsledku toho sa séria (41.2) rovnomerne zbieha v intervale [-ρ, ρ] podľa vety 40.1. Z voľby ρ vyplýva, že interval rovnomernej konvergencie - ( - R, R. ), podľa potreby.

Dôsledok 1 ... V každom segmente, ktorý leží úplne v intervale konvergencie, je súčet sérií (41,2) spojitou funkciou.

Dôkaz.

Pojmy radu (41.2) sú spojité funkcie a rady sa rovnomerne zbiehajú v uvažovanom segmente. Potom kontinuita jeho súčtu vyplýva z vety 40.2.

Dôsledok 2. Ak limity integrácie α, β ležia v intervale konvergencie výkonových radov, potom integrál súčtu radu je rovný súčtu integrálov pojmov radu:

(41.5)

Dôkaz tohto tvrdenia vyplýva z vety 40.3.

Veta 41,3. Ak má séria (41.2) interval konvergencie (- R, R), potom séria

φ (x) = a 1 + 2 a 2 x + 3 a 3 x ² +… + na n x n- 1 +…, (41,6)

získaný časovo rozlíšenou diferenciáciou radu (41.2), má rovnaký konvergenčný interval (- R, R). Kde

φ΄ (x) = s΄ (x) pre | x |< R , (41.7)

to znamená, že v rámci konvergenčného intervalu je derivácia súčtu výkonových radov rovná súčtu radu získaného jeho diferenciáciou medzi termínmi.

Dôkaz.

Vyberme ρ: 0< ρ < R и ζ: ρ < ζ < R ... Potom sa séria zbližuje, teda ak| x | ≤ ρ, potom

Kde teda termíny radu (41,6) sú v absolútnej hodnote menšie ako členy kladného radu, ktorý konverguje podľa d'Alembertovho znamienka:

to znamená, že je to majorant pre rad (41.6) pre. Preto sa rad (41.6) konverguje rovnomerne na [-ρ, ρ]. V dôsledku toho platí rovnosť (41,7) podľa vety 40,4. Z voľby ρ vyplýva, že séria (41,6) konverguje v ktoromkoľvek vnútornom bode intervalu (- R, R).

Dokážme, že mimo tohto intervalu sa séria (41,6) rozchádza. Skutočne, keby sa zbiehala pri x 1> R. , potom ho integrujte termín po termíne do intervalu (0, x 2), R.< x 2 < x 1 , dostali by sme, že séria (41.2) konverguje v bode x 2 , čo je v rozpore s hypotézou vety. Veta je teda úplne dokázaná.

Komentovať ... Série (41,6) je možné zase rozlišovať podľa výrazov a túto operáciu opakovať toľkokrát, koľkokrát chcete.

Výkon: ak sa rad výkonov zbieha v intervale (- R, R. ), potom je jeho súčet funkcia, ktorá má v rámci konvergenčného intervalu deriváty ľubovoľného poradia, z ktorých každý je súčtom radu získaného z pôvodného pomocou diferenciácie medzi jednotlivými termínmi zodpovedajúceho počtu krát; v tomto prípade je interval konvergencie pre sériu derivátov akéhokoľvek rádu (- R, R).

Katedra informatiky a vyššej matematiky KSPU

Funkčný rozsah sa nazýva formálne písomný prejav

u1 (X) + u 2 (X) + u 3 (X) + ... + u n ( X) + ... , (1)

kde u1 (X), u 2 (X), u 3 (X), ..., u n ( X), ... - postupnosť funkcií na nezávislej premennej X.

Skrátený zápis funkčného radu so sigma :.

Príklady funkčné rady môže slúžiť :

(2)

(3)

Zadaním nezávislej premennej X nejaký význam X0 a jeho nahradením do funkčného radu (1) získame číselný rad

u1 (X 0 ) + u 2 (X 0 ) + u 3 (X 0 ) + ... + u n ( X 0 ) + ...

Ak sa výsledný číselný rad zbieha, potom sa hovorí, že funkčný rad (1) konverguje pre X = X0 ; ak sa líši, čo sa hovorí, že séria (1) sa líši v X = X0 .

Príklad 1. Skúmajte konvergenciu funkčných radov(2) pre hodnoty X= 1 a X = - 1 .
Riešenie. O X= 1 dostaneme číselný rad

ktorá sa zbieha na základe Leibniz. O X= - 1 dostaneme číselný rad

,

ktorý sa líši ako súčin odlišných harmonických radov o - 1. Séria (2) teda konverguje pre X= 1 a rozchádza sa o X = - 1 .

Ak sa takáto kontrola konvergencie funkčného radu (1) vykonáva so zreteľom na všetky hodnoty nezávislej premennej z oblasti jej členov, body tejto oblasti sú rozdelené do dvoch množín: pre hodnoty X v jednom z nich sa série (1) zbiehajú a v druhom sa odlišujú.

Súbor hodnôt nezávislej premennej, pre ktorú funkčná rada konverguje, sa nazýva jej konvergenčná doména .

Príklad 2. Nájdite oblasť konvergencie funkčného radu

Riešenie. Členy radu sú definované v celom číselnom rade a so menovateľom tvoria geometrický priebeh q= hriech X... Séria sa preto zbieha, ak

a rozchádza sa, ak

(hodnoty nie sú možné). Ale pre hodnoty a pre iné hodnoty X... V dôsledku toho sa séria zbližuje pre všetky hodnoty X, okrem. Oblasťou jej konvergencie je celá číselná os, s výnimkou týchto bodov.

Príklad 3. Nájdite oblasť konvergencie funkčného radu

Riešenie. Členy radu tvoria so menovateľom geometrickú postupnosť q= ln X... Séria sa preto zbieha, ak alebo odkiaľ. Toto je oblasť konvergencie tejto série.

Príklad 4. Skúmajte konvergenciu funkčných radov

Riešenie. Zoberme si ľubovoľnú hodnotu. S touto hodnotou dostaneme číselný rad

(*)

Nájdite hranicu jeho spoločného termínu

V dôsledku toho sa séria (*) líši pre ľubovoľne zvolený, t.j. za akúkoľvek hodnotu X... Jeho doménou konvergencie je prázdna množina.

Rovnomerná konvergencia funkčného radu a jeho vlastností

Prejdeme k konceptu rovnomerná konvergencia funkčných radov ... Nechaj byť s(X) je súčtom tejto série a sn ( X) - súčet n prví členovia tejto série. Funkčný rozsah u1 (X) + u 2 (X) + u 3 (X) + ... + u n ( X) + ... sa nazýva rovnomerne konvergujúca v segmente [ a, b] ak pre ľubovoľne malé číslo ε > 0 existuje také číslo N.že pre všetkých n ≥ N. nerovnosť

|s(X) − s n ( X)| < ε

pre hocikoho X zo segmentu [ a, b] .

Vyššie uvedenú vlastnosť je možné geometricky znázorniť nasledovne.

Zoberme si graf funkcie r = s(X) ... Okolo tejto krivky postavíme pás šírky 2. ε n, to znamená, že zostrojíme krivky r = s(X) + ε n a r = s(X) − ε n(na obrázku nižšie sú zelené).

Potom pre akékoľvek ε n funkčný graf sn ( X) bude ležať úplne v uvažovanom páse. Rovnaké pásmo bude obsahovať grafy všetkých nasledujúcich čiastkových súčtov.

Všetky konvergujúce funkčné série, ktoré nemajú vyššie opísanú vlastnosť, nie sú rovnomerne konvergujúce.

Zvážte ešte jednu vlastnosť rovnomerne konvergujúcich funkčných sérií:

súčet série spojitých funkcií, ktoré sa rovnomerne zbiehajú v určitom intervale [ a, b], je funkcia, ktorá je v tomto segmente spojitá.

Príklad 5. Určte, či je súčet funkčných radov spojitý

Riešenie. Nájdite sumu n prví členovia tejto série:

Ak X> 0, potom

,

keby X < 0 , то

keby X= 0, potom

A preto .

Náš výskum ukázal, že súčet tejto série je nespojitá funkcia. Jeho graf je znázornený na obrázku nižšie.

Weierstrassov test na rovnomernú konvergenciu funkčných radov

K kritériu Weierstrass pristupujeme prostredníctvom konceptu zväčšiteľnosť funkčných sérií ... Funkčný rozsah

u1 (X) + u 2 (X) + u 3 (X) + ... + u n ( X) + ...

Oblasť konvergencie Funkčný rad A je rad členov, z ktorých sú funkcie / definované na nejakej množine E numerickej osi. Napríklad termíny radu sú definované na intervale a termíny radu sú definované na intervale Funkčný rad (1) sa nazýva konvergentný v bode X0 € E, ak FUNKČNÁ SÉRIA konverguje Doména konvergencie Rovnomerná konvergencia Weierstrass test Vlastnosti rovnomerne konvergentných funkčných radov numerických radov Ak sa séria (1) zbieha v každom bode x množiny DCE a rozchádza sa v každom bode, ktorý nepatrí do množiny D, potom sa hovorí, že séria konverguje v množine D a D sa nazýva doména konvergencie radu. Séria (1) sa nazýva absolútne konvergentná v množine D, ak séria konverguje k tejto množine. V prípade konvergencie radu (1) v množine D bude jej súčet S funkciou definovanou na D, Oblasť konvergencie niektorých funkčné série možno nájsť pomocou známych dostatočných kritérií stanovených pre série s kladnými pojmami, napríklad Dupamberov test, Cauchyho test. Príklad 1. Nájdite oblasť konvergencie radu M Pretože číselný rad konverguje pre p> 1 a diverguje pre p> 1, potom nastavením p - Igx získame tento rad. ktoré budú konvergovať pri Igx> Ц t.j. ak x> 10, a rozchádzajú sa pri Igx ^ 1, t.j. o 0< х ^ 10. Таким образом, областью сходимости ряда является луч Пример 2. Найти область сходимости ряда 4 Рассмотрим ряд Члены этого ряда положительны при всех значениях х. Применим к нему признак Даламбера. Имеем пе При ех < 1. т.е. при, этот ряд будет сходиться. Следовательно, заданный ряд сходится абсолютно на интервале При х > 0 riadkov sa líši, pretože Л =. Divergencia radu pri x = 0 je zrejmá. Príklad 3. Nájdite doménu konvergencie radu Termíny danej série sú na množine definované a spojité. Pri použití kritéria Kosh a nájdeme pre akékoľvek. V dôsledku toho sa séria líši pre všetky hodnoty x. Označíme Sn (x) n -tý parciálny súčet funkčných radov (1). Ak táto séria konverguje k množine D a jej súčet sa rovná 5 (g), potom ju možno reprezentovať ako kde je súčet sérií konvergujúcich k množine D, ktorá sa nazýva n -tý zvyšok funkčnej série (1 ). Pre všetky hodnoty х € D platí vzťah a preto. to znamená, že zvyšok Rn (x) konvergentného radu má tendenciu k nule ako n oo, bez ohľadu na x 6 D. Rovnomerná konvergencia Medzi všetkými konvergujúcimi funkčnými radmi majú dôležitú úlohu takzvané jednotne konvergentné rady. Nech je daná funkčná séria konvergujúca k množine D, ktorej súčet sa rovná S (x). Vezmite jeho n-tú definíciu čiastkového súčtu. Funkčné rady FUNKČNÉ SÉRIE Konvergenčná doména Rovnomerná konvergencia Weierstrassov test Vlastnosti rovnomerne konvergujúcich funkčných radov sa nazývajú rovnomerne konvergujúce na množine С1), ak pre akékoľvek e> 0 existuje číslo λ> 0 také, že nerovnosť platí pre všetky čísla n> N a pre všetky x zo súboru fI. Komentovať. Tu je číslo N rovnaké pre všetkých x 10 €, t.j. nezávisí od z, ale závisí od voľby čísla e, takže píšu N = N (e). Rovnomerná konvergencia funkčného radu / n (®) k funkcii S (x) na množine ft sa často označuje takto: Definíciu rovnomernej konvergencie radu / n (x) na množine ft je možné zapísať kratšie pomocou logických symbolov: Vysvetlíme geometrický význam funkčného rozsahu jednotnej konvergencie. Vezmeme ako množinu ft segment [a, 6] a zostrojíme grafy funkcií. Nerovnosť |, ktorá platí pre čísla n> N a pre všetky a; G [a, b], je možné zapísať v nasledujúcom tvare. Získané nerovnosti ukazujú, že grafy všetkých funkcií y = Sn (x) očíslované n> N budú úplne uzavreté v pásme ζ ohraničenom krivkami y = S (x) - e a y = 5 (g) + e (obr. 1). Príklad 1 rovnomerne konverguje k segmentu Tento rad sa strieda so znamienkami, spĺňa podmienky Leibnizovho testu pre akékoľvek x € [-1,1], a preto konverguje k segmentu (-1,1]. Nech S (x ) je jeho súčet a Sn (x) - jeho n -tý parciálny súčet Zvyšok radu v absolútnej hodnote nepresahuje absolútnu hodnotu jeho prvého členu: a keďže vezmite akékoľvek e. Potom bude nerovnosť | splnená, ak . Z toho zistíme, že n> 1. Ak vezmeme číslo (tu [a] označuje najväčšie celé číslo nepresahujúce a), potom nerovnosť | f bude platiť pre všetky čísla n> N a pre všetky x € [-1,1). To znamená, že tento rad sa rovnomerne zbieha na segmente [-1,1). I. Nie všetky funkčné rady konvergujúce na množinu D sa rovnomerne zbiehajú na príklade 2. Ukážme, že série konvergujú na segmente, ale nie rovnomerne. 4 Vypočítajme n -tý čiastkový súčet £ „(*) radu. Máme kde Táto séria konverguje na segment a jeho súčet, ak je absolútna hodnota rozdielu S (x) - 5 „(x) (zvyšok radu) rovná. Vezmite číslo e také, že. Vyriešme nerovnosť vzhľadom na n. Máme, odkiaľ (pretože a pri delení Inx sa znamienko nerovnosti zmení na opak). Nerovnosť bude splnená pre. Preto také číslo N (e) nezávislé od x také, aby nerovnosť platila pre každého) naraz pre všetky x zo segmentu. , neexistuje. Ak nahradíme segment 0 menším segmentom, kde, potom v poslednom uvedenom poradí budú dané rady konvergovať k funkcii S0 rovnomerne. Skutočne, pre, a teda pre všetkých x naraz §3. Weierstrassov test Dostatočné kritérium rovnomernej konvergencie funkčného radu poskytuje Weierstrassova veta. Veta 1 (Weierstrassov test). Predpokladajme, že pre všetky x z množiny Q termíny funkčného radu nepresahujú v absolútnej hodnote zodpovedajúce termíny konvergujúceho numerického radu = 1 s kladnými členmi, to znamená pre všetky x ∈ Q. Potom funkčný rad (1 ) na súprave konverguje absolútne a rovnomerne ... A Tek, ako v hypotéze vety termíny radu (1) spĺňajú podmienku (3) na celom súbore Q, potom podľa porovnávacieho kritéria konverguje rad 2 \ fn (x) \ pre akékoľvek x ∈ U , a preto sa séria (1) zbieha absolútne. Ukážme rovnomernú konvergenciu radu (1). Označme Sn (x) a čiastkové súčty radu (1) a (2). Máme Vezmite akékoľvek (ľubovoľne malé) číslo e> 0. Potom konvergencia číselného radu (2) znamená existenciu čísla N = N (e) také, že v dôsledku toho -e pre všetky čísla n> N (e ) a pre všetky xbn, t.j. rada (1) sa zbieha jednotne na množinu P. Poznámka. Číselný rad (2) sa často nazýva majorizácia alebo majorant pre funkčné rady (1). Príklad 1. Preskúmajte sériu kvôli rovnomernej konvergencii. Nerovnosť platí pre všetky. a pre všetkých. Číselný rad sa zbieha. Na základe kritéria Weierstrass sa uvažovaná funkčná rada absolútne a rovnomerne zbieha na celej osi. Príklad 2. Preskúmajte sériu kvôli rovnomernej konvergencii Termíny radu sú definované a spojité v intervale [-2,2 |. Pretože v intervale [-2,2) pre akékoľvek prirodzené n, potom teda nerovnosť platí pre. Pretože číselné rady konvergujú, potom podľa kritéria Weierstrassovej pôvodná funkčná rada konverguje v segmente absolútne a jednotne. Komentovať. Funkčné rady (1) sa môžu na súbore Piv zbiehať rovnomerne v prípade, že neexistuje žiadna číselná väčšia skupina (2), tj. Weierstrassov test je iba dostatočným kritériom rovnomernej konvergencie, ale nie je potrebný. Príklad. Ako je uvedené vyššie (príklad), séria konverguje rovnomerne na segment 1-1,1]. Neexistuje však pre neho žiadna majorizujúca konvergentná séria (2). Skutočne platí, že pre všetky prirodzené n a pre všetky x ∈ [-1,1) platí nerovnosť a rovnosť sa dosiahne pri. Preto podmienky požadovanej väčšinovej série (2) musia určite spĺňať podmienku, ale číselné rady FUNKČNÉ SÉRIE Konvergenčná oblasť Rovnomerná konvergencia Weierstrassov test Vlastnosti rovnomerne konvergujúcich funkčných radov sa líšia. To znamená, že aj série £ op sa budú líšiť. Vlastnosti rovnomerne konvergujúcich funkčných radov Rovnomerne konvergujúce funkčné rady majú množstvo dôležitých vlastností. Veta 2. Ak sú všetky členy radu konvergujúce rovnomerne na interval [a, b] vynásobené rovnakou funkciou g (x) ohraničenou na [a, 6], potom výsledná funkčná rada konverguje rovnomerne ďalej. Predpokladajme, že v intervale [a, b \ séria £ fn (x) konverguje rovnomerne na funkciu 5 (x) a funkcia g (x) je ohraničená, to znamená, že existuje konštanta C> 0 taká, že podľa definícia rovnomernej konvergencie radu pre akékoľvek číslo e> 0, existuje číslo N také, že pre všetky n> N a pre všetky x ∈ [a, b] platí nerovnosť, kde 5n (ar) je čiastočná súčet uvažovaného radu. Preto budeme mať pre kohokoľvek. séria konverguje rovnomerne na [a, b | k funkcii Veta 3. Predpokladajme, že všetky členy fn (x) funkčného radu sú spojité a rady sa rovnomerne zbiehajú na intervale [a, b \. Potom je súčet S (x) radu v tomto segmente spojitý. M Vezmite dva segmenty ľubovoľných bodov + sekeru na segmente [o, b]. Pretože táto séria konverguje rovnomerne na segment [a, b], potom pre akékoľvek číslo e> 0 existuje číslo N = N (e) také, že pre všetky n> N platia nerovnosti, kde 5n (x) sú čiastkové súčty radu fn (x). Tieto čiastkové súčty Sn (x) sú spojité v intervale [a, 6] ako súčet konečne mnohých funkcií fn (x) spojitých na [a, 6). Preto pre pevné číslo nie> N (e) a dané číslo e existuje číslo 6 = 6 (e)> 0 také, že pre prírastok Ax spĺňajúci podmienku | platí nerovnosť. Prírastok AS súčet S (x) môže byť reprezentovaný v nasledujúcej forme: odkiaľ. Ak vezmeme do úvahy nerovnosti (1) a (2), pre prírastky Ax spĺňajúce podmienku | dostaneme To znamená, že súčet Six) je v bode x spojitý. Pretože x je ľubovoľný bod segmentu [a, 6], potom 5 (x) je spojité na | a, 6 |. Komentovať. Funkčná séria, ktorej členy sú spojité na segmente [a, 6), ale ktoré konvergujú k (a, 6] nerovnomerne, môže mať nesúvislý súčet ako v príklade 1. Uvažujme funkčnú sériu na segmente | 0,1) . Vypočítajme jeho n-tý parciálny súčet, preto je na segmente nespojitý, aj keď termíny radu sú na ňom spojité. Na základe osvedčenej vety nie je táto séria rovnomerne konvergentná v intervale. Príklad 2. Uvažujme rad, Ako je uvedené vyššie, táto séria konverguje pre, séria bude konvergovať rovnomerne podľa Weierstrassovho kritéria, pretože 1 a číselný rad sa zbiehajú. Preto pre akékoľvek x> 1 je súčet tejto série spojitý. Komentovať. Táto funkcia sa nazýva Rímska funkcia (táto funkcia hrá v teórii čísel dôležitú úlohu). Veta 4 (o dočasnej integrácii funkčného radu). Predpokladajme, že všetky členy fn (x) radu sú spojité a rady sa v segmente [a, b] rovnomerne zbiehajú na funkciu S (x). Potom platí rovnosť Vďaka spojitosti funkcií fn (x) a rovnomernej konvergencii tohto radu na intervale [a, 6] je jeho súčet S (x) spojitý, a preto integrovateľný ďalej. Uvažujme rozdiel Z rovnomernej konvergencie radu na [o, b] vyplýva, že pre akékoľvek e> 0 existuje číslo N (e)> 0 také, že pre všetky čísla n> N (e) a pre všetky x ∈ [a, 6] Ak rad fn (0 nie je rovnomerne konvergentný, potom ho vo všeobecnosti nemožno integrovať z hľadiska výrazu, tj. veta 5 (o diferenciácii funkčného radu z hľadiska výrazov) Nechajte všetky termíny konvergujúceho radu 00 majú spojité deriváty a séria zložená z týchto derivátov sa zbieha rovnomerne v intervale [a, b]. Potom v každom bode platí rovnosť, to znamená, že daný rad je možné diferencovať podľa pojmu. Zoberme si akékoľvek dva body. Potom podľa vety 4 máme funkciu o- (x) spojitú ako súčet rovnomerne konvergujúcich sérií spojitých funkcií. Preto diferenciáciou rovnosti získame Cvičenia Nájdi oblasti konvergencie z týchto funkčných radov: Weierstrassovým testom ukážte rovnomernú konvergenciu týchto funkčných radov v uvedených intervaloch:

Téma 2. Funkčné rady. Silová séria

2.1. Funkčný rad

Doteraz sme zvažovali sériu čísel, ktoré boli členmi. Teraz sa obrátime na štúdium série, ktorej členmi sú funkcie.

Funkčný rozsah nazývaná séria

ktorých členy sú funkciami rovnakého argumentu definovaného na jednej množine E.

Napríklad,

1.
;

2.
;

Vzhľadom na argument NS nejaká číselná hodnota
,
, potom dostaneme číselný rad

ktoré sa môžu zbiehať (absolútne konvergovať) alebo sa môžu rozchádzať.

Ak o
výsledné číselné rady sa zbiehajú, potom bod
zavolalkonvergenčný bod funkčný rozsah. Zhromažďovanie všetkých bodov konvergencie sa nazývakonvergenčná doména funkčný rozsah. Označujeme región konvergencie NS očividne,
.

Ak pre numerické kladné rady je položená otázka: „Zbiera sa rad alebo rozchádza?“ Pod čím NS?».

Funkčný rozsah
ustanovuje právo, podľa ktorého je každá hodnota argumentu
,
, sa do korešpondencie vloží číslo rovnajúce sa súčtu číselných radov
... Teda na scéne NS funkcia je nastavená
, ktorá sa volá súčet funkčných radov.

Príklad 16.

Nájdite oblasť konvergencie funkčnej série

.

Riešenie.

Nechaj byť NS- pevné číslo, potom možno tento rad považovať za číselný rad, znamienko pozitívne na
a striedavo o
.

Zostavme sériu absolútnych hodnôt členov tejto série:

t.j. pre akúkoľvek hodnotu NS táto hranica je menšia ako jedna, čo znamená, že táto séria konverguje a absolútne (pretože sa skúmala séria absolútnych hodnôt členov radu) na celej číselnej osi.

Doménou absolútnej konvergencie je teda množina
.

Príklad 17.

Nájdite oblasť konvergencie funkčného radu
.

Riešenie.

Nechaj byť NS- pevné číslo,
, potom možno tento rad považovať za číselný rad, znamienko pozitívne na
a striedavo o
.

Zvážte sériu absolútnych hodnôt členov tejto série:

a naneste naň znak DAlembert.

Na základe DAlemberta sa séria zbieha, ak je hodnota limitu menšia ako jedna, t.j. táto séria sa zblíži, ak
.

Po vyriešení tejto nerovnosti dostaneme:


.

Séria teda zostavená z absolútnych hodnôt členov tejto série konverguje, čo znamená, že pôvodná séria sa absolútne zbieha a pri
táto séria sa líši.

O
séria sa môže zbiehať alebo rozchádzať, pretože pri týchto hodnotách NS hodnota limitu sa rovná jednej. Preto dodatočne skúmame konvergenciu série bodov
a
.

Náhrada do tohto riadka
, dostaneme číselný rad
, o ktorom je známe, že ide o harmonickú divergentnú sériu, čo znamená, že pointa
- bod divergencie danej série.

O
získa sa striedajúci sa číselný rad

o ktorom je známe, že sa podmienene zbieha (pozri príklad 15), čo znamená, že bod
- bod podmienenej konvergencie radu.

Oblasť konvergencie tejto série a série teda konverguje absolútne na.

Funkčný rozsah

zavolalmajorizovaný v nejakej oblasti variácií x, ak existuje taká konvergujúca znamienko-pozitívna séria

,

že pre všetky x z daného regiónu podmienka
o
... Riadok
zavolalmajorant.

Inými slovami, séria je majorizovaná, ak každý z jej výrazov v absolútnej hodnote nie je väčší ako zodpovedajúci člen niektorých konvergujúcich znakovo-pozitívnych radov.

Napríklad séria

je zameraný na akékoľvek NS pretože pre všetkých NS vzťah platí

o
,

a číslo je známe, že je konvergentný.

VetaWeierstrass

Séria dominujúca v určitej oblasti sa v tejto oblasti absolútne zbieha.

Uvažujme napríklad o funkčnej sérii
... Tejto sérii dominuje at
od o
členovia radu neprekračujú zodpovedajúce členy kladného radu ... V dôsledku toho podľa Weierstrassovej vety uvažovaná funkčná séria konverguje absolútne pre
.

2.2. Silová séria. Ábelova veta. Konvergenčná doména mocninovej série

Spomedzi celej škály funkčných sérií sú z hľadiska praktickej aplikácie najdôležitejšie silové a trigonometrické rady. Pozrime sa na takéto riadky podrobnejšie.

Silová séria o stupne
sa nazýva funkčná séria formulára

kde - nejaké pevné číslo,
- čísla nazývané koeficienty radu.

O
získame mocninový rad v mocninách NS ktoré má formu

.

Pre jednoduchosť budeme uvažovať mocninové rady v mocninách NS, pretože z takejto série je ľahké získať sériu mocnin
namiesto toho nahradiť NS výraz
.

Jednoduchosť a dôležitosť triedy výkonových radov je daná predovšetkým skutočnosťou, že čiastočný súčet výkonových radov je

je polynóm - funkcia, ktorej vlastnosti sú dobre študované a ktorej hodnoty sa dajú ľahko vypočítať iba pomocou aritmetických operácií.

Pretože výkonové rady sú špeciálnym prípadom funkčných radov, je potrebné pre ne nájsť aj oblasť konvergencie. Na rozdiel od oblasti konvergencie ľubovoľného funkčného radu, ktorým môže byť množina ľubovoľného tvaru, má oblasť konvergencie mocninového radu dobre definovaný tvar. Svedčí o tom nasledujúca veta.

VetaÁbel.

Ako mocnina
konverguje k nejakej hodnote
, potom konverguje a absolútne pre všetky hodnoty x, ktoré spĺňajú podmienku
... Ak sa rad výkonov líši o nejakú hodnotu
, potom sa líši pre hodnoty spĺňajúce podmienku
.

Z Ábelovej vety to vyplýva všetky body konvergencie mocninového radu v mocninách NS nachádzajúce sa od pôvodu nie sú ďalej než ktorýkoľvek z bodov divergencie. Body konvergencie zrejme vyplňujú určitú medzeru zameranú na pôvod. veta o doméne konvergencie mocninového radu platí.

Veta.

Pre akékoľvek výkonové rady
existuje čísloR. (R.>0)taký, že pre všetkých x ležiacich vo vnútri intervalu
, séria konverguje absolútne a pre všetkých x ležiacich mimo interval
, sa séria rozchádza.

ČísloR.zavolalpolomer konvergencie výkonový rad a interval
– konvergenčný interval mocninový rad v mocninách x.

Všimnite si, že veta nehovorí nič o konvergencii radu na koncoch intervalu konvergencie, t.j. v bodoch
... V týchto bodoch sa rôzne výkonové rady správajú odlišne: séria sa môže zbiehať (absolútne alebo podmienene) alebo sa môže líšiť. Preto by sa konvergencia sérií v týchto bodoch mala kontrolovať priamo podľa definície.

V špeciálnych prípadoch môže byť polomer konvergencie radu nula alebo nekonečno. Ak
, potom rad síl v mocninách NS konverguje iba v jednom bode
; keby
, potom sa výkonová rada zbieha na celej číselnej osi.

Ešte raz si všimnite, že výkonová rada
o stupne
možno redukovať na výkonovú sériu
nahradením
... Ak riadok
konverguje k
, t.j. pre
, potom po reverznej výmene dostaneme

 alebo
.

Teda interval konvergencie výkonových radov
má formu
... Bod sa volajú centrum konvergencie... Kvôli prehľadnosti je obvyklé znázorniť konvergenčný interval na číselnej osi (obrázok 1)

Konvergenčná doména teda pozostáva z konvergenčného intervalu, do ktorého je možné body sčítať
ak sa séria v týchto bodoch zbieha. Konvergenčný interval je možné nájsť priamou aplikáciou D'Alembertovho kritéria alebo radikálneho Cauchyho kritéria na sériu zloženú z absolútnych hodnôt členov danej série.

Príklad 18.

Nájdite oblasť konvergencie série
.

Riešenie.

Táto séria je výkonová séria v stupňoch NS, t.j.
... Uvažujte sériu zloženú z absolútnych hodnôt členov tejto série a použite d'Alembertov test.

Séria sa bude zbiehať, ak je hodnota limitu menšia ako 1, t.j.

, kde
.

Interval konvergencie tejto série
polomer konvergencie
.

Skúmame konvergenciu radu na koncoch intervalu, v bodoch
... Nahradením hodnoty v tomto riadku
, dostávame sériu

.

Výsledná séria je teda harmonickou divergentnou sériou v bode
rad sa rozchádza, takže pointa
nie je zahrnutý v regióne konvergencie.

O
dostávame striedavú sériu

,

ktorý je podmienene konvergentný (príklad 15), teda pointa
– konvergenčný bod (podmienený).

Región konvergencie radu
, a v bode
séria konverguje podmienene a v iných bodoch - absolútne.

Úvahy použité na vyriešenie príkladu je možné zovšeobecniť.

Zvážte výkonovú radu

Zostavíme sériu absolútnych hodnôt členov radu a použijeme na to Alamberov znak D.

Ak existuje (konečný alebo nekonečný) limit, potom podľa konvergenčných podmienok pre Alamberov atribút D bude séria konvergovať, ak

,

,

.

Z definície intervalu a polomeru konvergencie teda máme

Ak použijeme radikálne Cauchyovo kritérium a uvažujeme podobne, môžeme získať ďalší vzorec na nájdenie polomeru konvergencie.

Príklad 19

Riešenie.

Séria je exponenciálna v stupňoch NS. Aby sme našli konvergenčný interval, vypočítame polomer konvergencie pomocou vyššie uvedeného vzorca. Pre danú sériu má vzorec pre numerický koeficient formu

potom

Preto,

Pretože R. = , potom séria konverguje (a absolútne) pre všetky hodnoty NS, tí. konvergenčný región NS (–; +).

Všimnite si toho, že by bolo možné nájsť oblasť konvergencie bez použitia vzorcov, ale priamo pomocou Alambertovho testu D:

Pretože hodnota limitu nezávisí od NS a menej ako 1, potom séria konverguje pre všetky hodnoty NS, tí. o NS(-;+).

Príklad 20

Nájdite oblasť konvergencie série

1!(NS+5)+2!(NS + 5) 2 +3!(NS + 5) 3 +... + NS!(NS + 5) NS +...

Riešenie .

x + 5), tí. centrum konvergencie NS 0 = - 5. Numerický koeficient radu a NS = n!.

Nájdite polomer konvergencie série

.

Konvergenčný interval teda pozostáva z jedného bodu - centra konvergenčného intervalu x = - 5.

Príklad 21

Nájdite oblasť konvergencie série
.

Riešenie.

Táto séria je mocninová séria v silách ( NS–2), tí.

centrum konvergencie NS 0 = 2. Upozorňujeme, že séria je pre všetky fixné znamienka pozitívna NS, od výrazu ( NS- 2) povýšený na moc 2 NS. Uplatnime na sériu radikálne Cauchyovo kritérium.

Séria sa bude zbiehať, ak je hodnota limitu menšia ako 1, t.j.

,
,
,

teda polomer konvergencie
, potom konvergenčný integrál

,
.

Séria sa teda úplne zbieha pre NS
. Všimnite si toho, že konvergenčný integrál je symetrický vzhľadom na centrum konvergencie NS O = 2.

Skúmajme konvergenciu radu na koncoch konvergenčného intervalu.

Za predpokladu
, získame číselnú kladnú sériu

Použime potrebné konvergenčné kritérium:

preto sa číselný rad líši a bod
je bod divergencie. Všimnite si toho, že pri výpočte limitu bol použitý druhý pozoruhodný limit.

Za predpokladu
, dostávame rovnaké číselné rady (overte si to sami!), takže pointa
tiež nie je zahrnutý v konvergenčnom intervale.

Takže oblasť absolútnej konvergencie tejto série NS
.

2.3. Vlastnosti radu konvergentných síl

Vieme, že konečný súčet spojitých funkcií je spojitý; súčet diferencovateľných funkcií je diferencovateľný a derivácia súčtu sa rovná súčtu derivátov; konečnú sumu je možné integrovať termín po termíne.

Ukazuje sa, že vo všeobecnom prípade vlastnosti neplatia pre „nekonečné sumy“ funkcií - funkčných sérií.

Zoberme si napríklad rad funkcií

Je zrejmé, že všetci členovia série sú spojité funkcie. Nájdeme oblasť konvergencie tejto série a jej súčet. Aby sme to urobili, nájdeme čiastkové súčty série

potom súčet série

Teda suma S(NS) danej série ako limita postupnosti čiastkových súčtov existuje a je pre ňu konečná NS (-1;1), tento interval je teda oblasťou konvergencie radu. Jeho súčet je navyše nespojitou funkciou, pretože

Tento príklad teda ukazuje, že vo všeobecnom prípade vlastnosti konečných súčtov nemajú obdobu pre nekonečné súčty - série. Avšak v špeciálnom prípade funkčných radov - výkonových radov - súčty sú podobné vlastnostiam konečných súčtov.

- možno komplex nebude taký ťažký;) A názov tohto článku je tiež nelogický - série, o ktorých sa dnes bude diskutovať, pravdepodobne nie sú zložité, ale „vzácne zeminy“. Avšak ani študenti na čiastočný úväzok nie sú voči nim poistení, a preto sa zdá, že by to tak bolo doplnková činnosť treba brať s maximálnou vážnosťou. Koniec koncov, po vypracovaní si budete vedieť poradiť takmer s každou „beštiou“!

Začnime klasikou žánru:

Príklad 1

Najprv si všimnite, že toto NIE je séria energií (Pripomínam vám, že to tak vyzerá)... A za druhé, tu význam okamžite padne do oka, ktorý očividne nemôže vstúpiť do oblasti konvergencie série. A to je už malý úspech výskumu!

Ale napriek tomu, ako dosiahnuť veľký úspech? Ponáhľam sa, aby som vás potešil - také riadky je možné vyriešiť rovnako ako mocenský zákon- spoliehať sa na znak d'Alembert alebo radikálny znak Cauchy!

Riešenie: hodnota nie je zahrnutá v konvergenčnom rozsahu série. Toto je zásadný fakt a treba ho poznamenať!

Základný algoritmus funguje štandardným spôsobom. Pomocou d'Alembertovho testu nájdeme konvergenčný interval radu:

Séria sa zbieha pri. Zdvihnime modul hore:

Okamžite skontrolujme „zlý“ bod: hodnota nevstúpila do konvergenčnej oblasti série.

Skúmajme konvergenciu radu na „vnútorných“ koncoch intervalov:
Ak potom
Ak potom

Oba číselné rady sa líšia, pretože nie sú splnené nevyhnutné konvergenčné kritérium.

Odpoveď: oblasť konvergencie:

Urobme malú analytickú kontrolu. Nahraďme nejakú hodnotu zo správneho intervalu do funkčného radu, napríklad:
- zbieha sa d'Alembert.

V prípade substitúcie hodnôt z ľavého intervalu sa získajú aj konvergujúce rady:
Ak potom.

A nakoniec, ak, tak séria - naozaj sa rozchádza.

Niekoľko jednoduchých príkladov na zahriatie:

Príklad 2

Nájdite oblasť konvergencie funkčného radu

Príklad 3

Nájdite oblasť konvergencie funkčného radu

Buďte obzvlášť dobrí s „novým“ modul- dnes sa stretne 100 500 krát!

Stručné riešenia a odpovede na konci hodiny.

Použité algoritmy sa zdajú byť univerzálne a spoľahlivé, ale v skutočnosti to tak nie je - u mnohých funkčných sérií často „skĺznu“ alebo dokonca vedú k chybným záverom (a zvážim aj takéto príklady).

Drsnosť začína už na úrovni interpretácie výsledkov: zvážte napríklad sériu. Tu v limite získavame (overte si to sami), a teoreticky je potrebné dať odpoveď, že séria sa zbieha v jednom bode. Pointa je však „prehnaná“, čo znamená, že náš „pacient“ sa rozchádza všade!

A pre sériu „zrejmé“ riešenie „podľa Cauchyho“ neposkytuje vôbec nič:
- pre Ľubovoľnú hodnotu „x“.

A vzniká otázka, čo robiť? Použime metódu, ktorej bude venovaná hlavná časť hodiny! Možno to formulovať nasledovne:

Priama analýza numerických radov pri rôznych hodnotách

V skutočnosti sme to už začali robiť v Príklade 1. Najprv preskúmame niektoré konkrétne „x“ a zodpovedajúce číselné rady. Vyžaduje si to hodnotu:
- výsledný číselný rad sa líši.

A to okamžite vyvolá myšlienku: čo keď sa to isté stane v iných bodoch?
Skontrolujme to nevyhnutné kritérium pre konvergenciu série pre svojvoľný hodnoty:

Bod je účtovaný vyššie, pre všetky ostatné „x“ organizujeme druhá nádherná hranica:

Výkon: séria sa líši pozdĺž celého číselného radu

A toto riešenie je najfunkčnejšou možnosťou!

V praxi sa musí často porovnávať funkčný rozsah zovšeobecnené harmonické série :

Príklad 4

Riešenie: v prvom rade sa zaoberáme rozsah: v tomto prípade musí byť radikálny výraz striktne pozitívny a navyše musia existovať všetci členovia série, počnúc 1.. Z toho vyplýva, že:
... S týmito hodnotami sa získajú podmienene konvergujúce rady:
atď.

Iné „x“ nie sú vhodné, napríklad keď dostaneme nezákonný prípad, keď prví dvaja členovia série neexistujú.

To je všetko dobré, všetko je jasné, ale zostáva ešte jedna dôležitá otázka - ako správne vypracovať rozhodnutie? Navrhujem schému, ktorú možno žargónicky nazvať „prenos šípok“ do číselných radov:

Zvážte svojvoľný význam a skúmať konvergenciu číselných radov. Rutina Leibnizov znak:

1) Tento riadok sa strieda.

2) - členovia radu klesajú v absolútnej hodnote. Každý nasledujúci výraz v sérii má menšiu absolútnu hodnotu ako predchádzajúci: preto je pokles monotónny.

Záver: séria sa zbieha na základe Leibniza. Ako už bolo uvedené, konvergencia je tu podmienená - z toho dôvodu, že séria - rozchádza sa.

Len tak - úhľadne a správne! Pretože za „alfa“ sme šikovne skryli všetky prípustné číselné rady.

Odpoveď: funkčný rad existuje a konverguje podmienene pri.

Podobný príklad samostatného riešenia:

Príklad 5

Pozrite sa na konvergenciu funkčných sérií

Približný príklad dokončenia úlohy na konci hodiny.

Toľko k vašej „pracovnej hypotéze“! - funkčná séria konverguje k intervalu!

2) So symetrickým intervalom je všetko transparentné, uvažujeme svojvoľný hodnoty a dostaneme: - absolútne konvergujúce číselné rady.

3) A nakoniec „stred“. Aj tu je vhodné zvoliť dva intervaly.

Zvážte svojvoľný hodnota z intervalu a dostaneme číselný rad:

! Opäť - ak je to ťažké , nahraďte napríklad akékoľvek konkrétne číslo. Avšak ... chceli ste ťažkosti =)

Pre všetky hodnoty „en“ , znamená:
- teda tým porovnávacie kritérium séria konverguje spolu s nekonečne klesajúcou progresiou.

Pre všetky hodnoty "x" z intervalu, ktoré dostaneme - absolútne konvergujúce číselné rady.

Všetky X boli vyšetrené, X sú preč!

Odpoveď: oblasť konvergencie radu:

Musím povedať, nečakaný výsledok! A tiež treba dodať, že používanie znakov d'Alembert alebo Cauchy tu bude určite zavádzajúce!

Priame hodnotenie je „akrobacia“ matematickej analýzy, ale to samozrejme vyžaduje skúsenosti a niekde dokonca intuíciu.

Alebo možno niekto nájde cestu jednoduchšie? Napíšte! Mimochodom, existujú precedensy - čitatelia niekoľkokrát navrhli viac racionálne rozhodnutia a s potešením som ich publikoval.

Úspešné pristátie :)

Príklad 11

Nájdite oblasť konvergencie funkčného radu

Moja verzia riešenia je veľmi blízka.

Ďalšie hardcore nájdete na Oddiel VI (riadky) zbierka Kuznetsova (Problémy 11-13). Na internete sú hotové riešenia, ale tu som vám dlžný varovať- mnohé z nich sú neúplné, nesprávne alebo dokonca vo všeobecnosti chybné. A mimochodom, to bol jeden z dôvodov, prečo sa zrodil tento článok.

Zhrňme si tri lekcie a zorganizujme si súbor nástrojov. Takže:

Na nájdenie konvergenčného intervalu (intervalov) funkčného radu je možné použiť:

1) D'Alembertov znak alebo Cauchyov znak... A ak riadok nie je upokojiť- pri analýze výsledku získaného priamou substitúciou rôznych hodnôt dávame veľký pozor.

2) Kritérium jednotnej konvergencie Weierstrassu... Nezabúdajme!

3) Porovnanie s typickými číselnými radmi- pravidlá vo všeobecnom prípade.

Potom preskúmajte konce nájdených intervalov (V prípade potreby) a získame oblasť konvergencie radu.

Teraz máte k dispozícii dosť vážny arzenál, ktorý vám umožní zvládnuť takmer akúkoľvek tematickú úlohu.

Prajem vám úspech!

Riešenia a odpovede:

Príklad 2: Riešenie: hodnota nie je zahrnutá v konvergenčnom rozsahu série.
Používame znak d'Alembert:


Séria konverguje k:

Intervaly konvergencie funkčného radu sú teda: .
Pozrime sa na konvergenciu radu v koncových bodoch:
Ak potom ;
Ak potom .
Oba číselné rady sa líšia, tk. požadované konvergenčné kritérium nie je splnené.

Odpoveď : oblasť konvergencie: