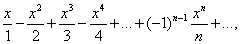
lukhov Yu.P. Lecture notes on higher mathematics. Lecture number 42 5

Lecture 42

THEME: Functional ranks

Plan.

1. Functional rows. Convergence region.
2. Uniform convergence. Weierstrass sign.
3. Properties of uniformly converging series: continuity of the sum of a series, term-by-term integration and differentiation.
4. Power series. Abel's theorem. Convergence region of the power series. Convergence radius.
5. Basic properties of power series: uniform convergence, continuity and infinite differentiability of the sum. Term-by-term integration and differentiation of power series.

Functional rows. Convergence region

Definition 40.1. An infinite sum of functions

u 1 (x) + u 2 (x) +… + u n (x) +…, (40.1)

where u n (x) = f (x, n) is called functional range.

If you set a specific numeric value NS , the series (40.1) will turn into a numerical series, and depending on the choice of the value NS such a series may converge or diverge. Only converging series are of practical value, so it is important to determine those values NS , at which the functional series becomes a converging numerical series.

Definition 40.2. Many meanings NS , when substituted into the functional series (40.1), a converging numerical series is obtained, is calledconvergence domainfunctional range.

Definition 40.3. Function s (x), defined in the region of convergence of the series, which for each value NS from the region of convergence is equal to the sum of the corresponding numerical series obtained from (40.1) for a given value x is called the sum of the functional series.

Example. Find the region of convergence and the sum of the functional series

1 + x + x ² + ... + x n + ...

When | x | ≥ 1 therefore the corresponding numerical series diverge. If

| x | < 1, рассматриваемый ряд представляет собой сумму бесконечно убывающей геометрической прогрессии, вычисляемую по формуле:

Consequently, the range of convergence of the series is the interval (-1, 1), and its sum has the indicated form.

Comment ... Just as for numerical series, you can introduce the concept of a partial sum of a functional series:

s n = 1 + x + x ² + ... + x n

and the remainder of the row: r n = s - s n.

Uniform convergence of a functional series

Let us first define the concept of uniform convergence of a numerical sequence.

Definition 40.4. Functional sequence f n (x) is called converging uniformly to the function f on the set X, if and

Remark 1. We will denote the usual convergence of a functional sequence and uniform convergence -.

Remark 2 ... We note once again the fundamental difference between uniform convergence and ordinary convergence: in the case of ordinary convergence, for the chosen value of ε, for each there exists your number N, for which at n> N inequality holds:

In this case, it may turn out that for a given ε, choose a common number N, ensuring the fulfillment of this inequality for any NS , impossible. In the case of uniform convergence, such a number N common to all x exists.

Let us now define the concept of uniform convergence of a functional series. Since each series corresponds to a sequence of its partial sums, the uniform convergence of the series is determined through the uniform convergence of this sequence:

Definition 40.5. The functional range is calleduniformly converging on the set X, if on X the sequence of its partial sums converges uniformly.

Weierstrass sign

Theorem 40.1. If the number series converges for all and for all n = 1, 2, ... the inequality holds, then the series converges absolutely and uniformly on the set NS.

Proof.

For any ε> 0 c there is such a number N, which is why

For residuals r n a number of fair estimates

Hence, therefore, the series converges uniformly.

Comment. The procedure for selecting a numerical series satisfying the conditions of Theorem 40.1 is usually called majorization , and this row itself - majorant for a given functional range.

Example. For a functional series, a majorant for any value NS is a converging positive series. Therefore, the original series converges uniformly at (-∞, + ∞).

Properties of uniformly converging series

Theorem 40.2. If the functions u n (x) are continuous for and the series converges uniformly on X, then its sum s (x) is also continuous at the point x 0.

Proof.

We choose ε> 0. Then, therefore, there is such a number n 0 that

- the sum of a finite number of continuous functions, thereforecontinuous at the point x 0. Therefore, there exists a δ> 0 such that Then we get:

That is, the function s (x) is continuous at x = x 0.

Theorem 40.3. Let the functions u n (x) are continuous on the segment [ a, b ] and the series converges uniformly on this segment. Then the series also converges uniformly on [ a, b] and (40.2)

(that is, under the conditions of the theorem, the series can be term-by-term integrated).

Proof.

By Theorem 40.2, the function s (x) = is continuous on [a, b ] and, therefore, is integrable on it, that is, the integral on the left-hand side of equality (40.2) exists. Let us show that the series converges uniformly to the function

We denote

Then for any ε there is a number N, which for n> N

Hence, the series converges uniformly, and its sum is equal to σ ( x) =.

The theorem is proved.

Theorem 40.4. Let the functions u n (x) continuously differentiable on the segment [ a, b ] and a series composed of their derivatives:

(40.3)

converges uniformly on [ a, b ]. Then, if the series converges at least at one point, then it converges uniformly on the whole [ a, b], its sum s (x) = is a continuously differentiable function and

(the series can be differentiated term by term).

Proof.

We define the function σ ( NS ) how. By Theorem 40.3, the series (40.3) can be term-by-term integrated:

The series on the right-hand side of this equality converges uniformly on [ a, b ] by Theorem 40.3. But the number series converges by the hypothesis of the theorem, therefore, the series also converges uniformly. Then the Function σ ( t ) is the sum of a uniformly convergent series of continuous functions on [ a, b ] and is therefore itself continuous. Then the function is continuously differentiable on [ a, b ], and, as required.

Definition 41.1. Power series is called a functional series of the form

(41.1)

Comment. By replacing x - x 0 = t series (41.1) can be reduced to the form; therefore, it suffices to prove all the properties of power series for series of the form

(41.2)

Theorem 41.1 (Abel's 1st theorem).If the power series (41.2) converges for x = x 0, then for any x: | x |< | x 0 | series (41.2) converges absolutely. If the series (41.2) diverges at x = x 0, then it diverges for any x: | x | > | x 0 |.

Proof.

If the series converges, then therefore there is a constant c> 0:

Consequently, the series for | x |<| x 0 | converges, since it is the sum of an infinitely decreasing geometric progression. Hence, the series for | x |<| x 0 | absolutely converges.

If it is known that series (41.2) diverges for x = x 0 , then it cannot converge for | x | > | x 0 | , since from what was proved earlier it would follow that it also converges at the point x 0.

Thus, if we find the largest of the numbers x 0 > 0 such that (41.2) converges for x = x 0, then the domain of convergence of this series, as follows from Abel's theorem, will be the interval (- x 0, x 0 ), possibly including one or both boundaries.

Definition 41.2. The number R ≥ 0 is called radius of convergencepower series (41.2) if this series converges, but diverges. Interval (- R, R) is called convergence interval series (41.2).

Examples.

1. To study the absolute convergence of the series, we use the d'Alembert criterion:. Consequently, the series converges only for NS = 0, and the radius of its convergence is 0: R = 0.
2. Using the same d'Alembert test, one can show that the series converges for any x, that is
3. For a series based on d'Alembert we get:

Therefore, at –1< x < 1 ряд сходится, при

x< -1 и x > 1 diverges. At NS = 1 we obtain a harmonic series, which, as is known, diverges, and for NS = -1 series converges conventionally on the basis of Leibniz. Thus, the radius of convergence of the series under consideration is R = 1, and the convergence interval is [-1, 1).

Formulas for determining the radius of convergence of a power series.

1. D'Alembert formula.

Consider a power series and apply the d'Alembert test to it: for the series to converge, it is necessary that. If exists, then the region of convergence is determined by the inequality, that is

- (41.3)

• d'Alembert formulato calculate the radius of convergence.

1. Cauchy-Hadamard formula.

Using the radical Cauchy criterion and arguing in a similar way, we find that we can define the convergence domain of a power series as a set of solutions to the inequality provided this limit exists, and, accordingly, find another formula for the radius of convergence:

(41.4)

• Cauchy-Hadamard formula.

Properties of power series.

Theorem 41.2 (Abel's 2nd theorem). If R Is the radius of convergence of the series (41.2) and this series converges at x = R , then it converges uniformly on the interval (- R, R).

Proof.

The positive series converges by Theorem 41.1. Consequently, the series (41.2) converges uniformly in the interval [-ρ, ρ] by Theorem 40.1. From the choice of ρ it follows that the interval of uniform convergence - (- R, R ), as required.

Corollary 1 ... On any segment that lies entirely within the interval of convergence, the sum of series (41.2) is a continuous function.

Proof.

The terms of the series (41.2) are continuous functions, and the series converges uniformly on the segment under consideration. Then the continuity of its sum follows from Theorem 40.2.

Corollary 2. If the limits of integration α, β lie within the interval of convergence of the power series, then the integral of the sum of the series is equal to the sum of the integrals of the terms of the series:

(41.5)

The proof of this statement follows from Theorem 40.3.

Theorem 41.3. If series (41.2) has an interval of convergence (- R, R), then the series

φ (x) = a 1 + 2 a 2 x + 3 a 3 x ² +… + na n x n- 1 +…, (41.6)

obtained by term-by-term differentiation of the series (41.2), has the same convergence interval (- R, R). Wherein

φ΄ (x) = s΄ (x) for | x |< R , (41.7)

that is, within the convergence interval, the derivative of the sum of the power series is equal to the sum of the series obtained by its term-by-term differentiation.

Proof.

Let us choose ρ: 0< ρ < R и ζ: ρ < ζ < R ... Then the series converges, therefore, that is, If| x | ≤ ρ, then

Where Thus, the terms of the series (41.6) are less in absolute value than the members of the positive series, which converges according to the d'Alembert sign:

that is, it is a majorant for the series (41.6) for Therefore, the series (41.6) converges uniformly on [-ρ, ρ]. Consequently, equality (41.7) is true by Theorem 40.4. It follows from the choice of ρ that series (41.6) converges at any interior point of the interval (- R, R).

Let us prove that outside this interval the series (41.6) diverges. Indeed, if it converged at x 1> R , then, integrating it term by term on the interval (0, x 2), R< x 2 < x 1 , we would get that series (41.2) converges at the point x 2 , which contradicts the hypothesis of the theorem. So, the theorem is completely proved.

Comment ... Series (41.6) can, in turn, be differentiated term by term and repeat this operation as many times as you like.

Output: if the power series converges on the interval (- R, R ), then its sum is a function that has derivatives of any order within the convergence interval, each of which is the sum of a series obtained from the original one using term-by-term differentiation the corresponding number of times; in this case, the interval of convergence for a series of derivatives of any order is (- R, R).

Department of Informatics and Higher Mathematics KSPU

Functional range is a formally written expression

u1 (x) + u 2 (x) + u 3 (x) + ... + u n ( x) + ... , (1)

where u1 (x), u 2 (x), u 3 (x), ..., u n ( x), ... - sequence of functions on the independent variable x.

Abbreviated notation of a functional series with sigma:.

Examples functional rows can serve :

(2)

(3)

By giving the independent variable x some meaning x0 and substituting it into the functional series (1), we obtain the number series

u1 (x 0 ) + u 2 (x 0 ) + u 3 (x 0 ) + ... + u n ( x 0 ) + ...

If the resulting number series converges, then the functional series (1) is said to converge for x = x0 ; if it diverges, which is said to be that series (1) diverges at x = x0 .

Example 1. Investigate the convergence of a functional series(2) for values x= 1 and x = - 1 .
Solution. At x= 1 we get a number series

which converges on the basis of Leibniz. At x= - 1 we get a number series

,

which diverges as the product of a diverging harmonic series by - 1. Thus, series (2) converges for x= 1 and diverges at x = - 1 .

If such a check for the convergence of the functional series (1) is carried out with respect to all values ​​of the independent variable from the domain of definition of its members, then the points of this domain are split into two sets: for the values x taken in one of them, series (1) converges, and in the other it diverges.

The set of values ​​of the independent variable for which the functional series converges is called its convergence domain .

Example 2. Find the region of convergence of a functional series

Solution. The members of the series are defined on the whole number line and form a geometric progression with the denominator q= sin x... Therefore, the series converges if

and diverges if

(values ​​are not possible). But for values ​​and for other values x... Consequently, the series converges for all values x, except . The area of ​​its convergence is the entire number line, with the exception of these points.

Example 3. Find the region of convergence of a functional series

Solution. The members of the series form a geometric progression with the denominator q= ln x... Therefore, the series converges, if, or, whence. This is the region of convergence of this series.

Example 4. Investigate the convergence of a functional series

Solution. Let's take an arbitrary value. With this value, we get a number series

(*)

Find the limit of its common term

Consequently, the series (*) diverges for an arbitrarily chosen one, i.e. for any value x... Its domain of convergence is an empty set.

Uniform convergence of a functional series and its properties

Let's move on to the concept uniform convergence of the functional series ... Let be s(x) is the sum of this series, and sn ( x) - sum n the first members of this series. Functional range u1 (x) + u 2 (x) + u 3 (x) + ... + u n ( x) + ... is called uniformly converging on the segment [ a, b] if for any arbitrarily small number ε > 0 there is such a number N that for all n ≥ N the inequality

|s(x) − s n ( x)| < ε

for anyone x from the segment [ a, b] .

The above property can be geometrically illustrated as follows.

Consider the graph of the function y = s(x) ... Let's build a strip of width 2 around this curve. ε n, that is, we will construct curves y = s(x) + ε n and y = s(x) − ε n(in the picture below they are green).

Then for any ε n function graph sn ( x) will lie entirely in the considered strip. The same band will contain graphs of all subsequent partial sums.

Any converging functional series that does not have the feature described above is non-uniformly converging.

Consider one more property of uniformly converging functional series:

the sum of a series of continuous functions converging uniformly on some interval [ a, b], is a function that is continuous on this segment.

Example 5. Determine if the sum of a functional series is continuous

Solution. Find the amount n the first members of this series:

If x> 0, then

,

if x < 0 , то

if x= 0, then

And therefore .

Our research has shown that the sum of this series is a discontinuous function. Its graph is shown in the figure below.

Weierstrass test for uniform convergence of function series

We approach the Weierstrass criterion through the concept majorizability of functional series ... Functional range

u1 (x) + u 2 (x) + u 3 (x) + ... + u n ( x) + ...

The region of convergence A functional series is a series of members of which are functions / defined on some set E of the numerical axis. For example, the terms of the series are defined on an interval, and the terms of the series are defined on an interval Functional series (1) is called convergent at the point X0 € E if the FUNCTIONAL SERIES converges Domain of convergence Uniform convergence Weierstrass test Properties of uniformly convergent functional series numerical series If series (1) converges at each point x of the set D C E and diverges at each point that does not belong to the set D, then the series is said to converge on the set D, and D is called the domain of convergence of the series. Series (1) is called absolutely convergent on the set D if the series converges on this set.In the case of convergence of the series (1) on the set D, its sum S will be a function defined on D, The region of convergence of some functional series can be found using the known sufficient criteria established for series with positive terms, for example, Dupamber's test, Cauchy's test. Example 1. Find the region of convergence of the series M Since the number series converges for p> 1 and diverges for p> 1, then, setting p - Igx, we obtain this series. which will converge at Igx> Ц i.e. if x> 10, and diverge at Igx ^ 1, i.e. at 0< х ^ 10. Таким образом, областью сходимости ряда является луч Пример 2. Найти область сходимости ряда 4 Рассмотрим ряд Члены этого ряда положительны при всех значениях х. Применим к нему признак Даламбера. Имеем пе При ех < 1. т.е. при, этот ряд будет сходиться. Следовательно, заданный ряд сходится абсолютно на интервале При х > 0 row diverges, since Л =. The divergence of the series at x = 0 is obvious. Example 3. Find the domain of convergence of a series The terms of a given series are defined and continuous on the set. Applying the criterion Kosh and, we find for any. Consequently, the series diverges for all values ​​of x. We denote by Sn (x) the nth partial sum of the functional series (1). If this series converges on the set D and its sum is equal to 5 (g), then it can be represented as where is the sum of the series converging on the set D, which is called the nth remainder of the functional series (1). For all values ​​of х € D the relation holds and therefore. that is, the remainder Rn (x) of a converging series tends to zero as n oo, whatever x 6 D. Uniform convergence Among all converging functional series, an important role is played by the so-called uniformly converging series. Let there be given a functional series converging on the set D whose sum is equal to S (x). Take its n-th partial sum Definition. Functional series FUNCTIONAL SERIES Convergence domain Uniform convergence The Weierstrass test Properties of uniformly converging functional series are called uniformly converging on the set С1) if for any e> 0 there is a number λ> 0 such that the inequality holds for all numbers n> N and for all x from the set fI. Comment. Here the number N is the same for all x € 10, i.e. does not depend on z, but depends on the choice of the number e, so they write N = N (e). The uniform convergence of the functional series / n (®) to the function S (x) on the set ft is often denoted as follows: The definition of the uniform convergence of the series / n (x) on the set ft can be written shorter with the help of logical symbols: Let us explain the geometrically meaning of uniform convergence functional range. We take as the set ft the segment [a, 6] and construct the graphs of the functions. Inequality |, which holds for numbers n> N and for all a; G [a, b], can be written in the following form The obtained inequalities show that the graphs of all functions y = Sn (x) with numbers n> N will be entirely enclosed within the ζ-band bounded by the curves y = S (x) - e and y = 5 (g) + e (Fig. 1). Example 1 converges uniformly on the segment This series is alternating with signs, satisfies the conditions of the Leibniz test for any x € [-1,1] and, therefore, converges on the segment (-1,1]. Let S (x) be its sum, and Sn (x) - its n-th partial sum The remainder of the series in absolute value does not exceed the absolute value of its first term: and since Take any e. Then the inequality | will be satisfied if. From this we find that n> 1. If we take a number (here [a] denotes the largest integer not exceeding a), then the inequality | f will be performed for all numbers n> N and for all x € [-1,1). This means that this series converges uniformly on the segment [-1,1). I. Not every function series converging on the set D is uniformly converging on Example 2. Let us show that the series converges on a segment, but not uniformly. 4 Let us calculate the nth partial sum £ „(*) of the series. We have Where This series converges on a segment and its sum if the absolute value of the difference S (x) - 5 „(x) (the remainder of the series) is equal to. Take a number e such that. Let Let us solve the inequality with respect to n. We have, whence (since, and when dividing by Inx, the inequality sign is reversed). The inequality will be fulfilled for. Therefore, such a number N (e) independent of x such that the inequality holds for each) at once for all x from the segment. , does not exist. If we replace the segment 0 with a smaller segment, where, then at the latter the given series will converge to the function S0 uniformly. Indeed, for, and therefore for all x at once §3. Weierstrass test A sufficient criterion for the uniform convergence of a functional series is given by the Weierstrass theorem. Theorem 1 (Weierstrass test). Suppose that for all x from the set Q the terms of the functional series do not exceed in absolute value the corresponding terms of the converging numerical series = 1 with positive terms, that is, for all x ∈ Q. Then the functional series (1) on the set converges absolutely and uniformly ... And Tek, as by the hypothesis of the theorem, the terms of the series (1) satisfy condition (3) on the whole set Q, then by the comparison criterion the series 2 \ fn (x) \ converges for any x ∈ U, and, therefore, the series (1) converges on Absolutely. Let us prove the uniform convergence of series (1). Let Denote by Sn (x) and an the partial sums of series (1) and (2), respectively. We have Take any (arbitrarily small) number e> 0. Then the convergence of the number series (2) implies the existence of a number N = N (e) such that, consequently, -e for all numbers n> N (e) and for all xbn , i.e. series (1) converges uniformly on the set P. Remark. Number series (2) is often called majorizing, or majorant, for functional series (1). Example 1. Investigate the series for uniform convergence. The inequality holds for all. and for everyone. The number series converges. By virtue of the Weierstrass criterion, the considered functional series converges absolutely and uniformly on the entire axis. Example 2. Investigate the series for uniform convergence. The terms of the series are defined and continuous on the interval [-2,2 |. Since on the interval [-2,2) for any natural n, then Thus, the inequality holds for. Since the number series converges, then according to the Weierstrass criterion, the original functional series converges absolutely and uniformly on a segment. Comment. Functional series (1) can converge uniformly on the set Piv in the case when there is no numerical majorant series (2), i.e., the Weierstrass test is only a sufficient criterion for uniform convergence, but it is not necessary. Example. As shown above (example), the series converges uniformly on the segment 1-1,1]. However, there is no majorizing convergent series (2) for it. Indeed, for all natural n and for all x ∈ [-1,1), the inequality holds, and the equality is attained at. Therefore, the terms of the required majorant series (2) must certainly satisfy the condition but the number series FUNCTIONAL SERIES Convergence region Uniform convergence Weierstrass test Properties of uniformly converging functional series diverge. This means that the series £ op will also diverge. Properties of uniformly converging functional series Uniformly converging functional series have a number of important properties. Theorem 2. If all the terms of a series converging uniformly on the interval [a, b] are multiplied by the same function g (x) bounded on [a, 6], then the resulting functional series converges uniformly on. Suppose that on the interval [a, b \ the series £ fn (x) converges uniformly to the function 5 (x), and the function g (x) is bounded, that is, there exists a constant C> 0 such that By the definition of the uniform convergence of the series for any number e> 0, there exists a number N such that for all n> N and for all x ∈ [a, b], the inequality holds where 5n (ar) is the partial sum of the series under consideration. Therefore, we will have for anyone. the series converges uniformly on [a, b | to a function Theorem 3. Suppose that all terms fn (x) of a functional series are continuous and the series converges uniformly on the interval [a, b \. Then the sum S (x) of the series is continuous on this segment. M Take two arbitrary points rig + Ax on the segment [o, b]. Since this series converges uniformly on the interval [a, b], then for any number e> 0 there is a number N = N (e) such that for all n> N the inequalities hold where 5n (x) are the partial sums of the series fn (x). These partial sums Sn (x) are continuous on the interval [a, 6] as the sums of a finite number of functions fn (x) continuous on [a, 6). Therefore, for a fixed number no> N (e) and a given number e, there is a number 6 = 6 (e)> 0 such that for the increment Ax satisfying the condition |, the inequality holds.The increment AS of the sum S (x) can be represented in the following form: from where. Taking into account inequalities (1) and (2), for the increments Ax satisfying the condition |, we obtain This means that the sum Six) is continuous at the point x. Since x is an arbitrary point of the segment [a, 6], then 5 (x) is continuous on | a, 6 |. Comment. A functional series whose terms are continuous on the segment [a, 6), but which converges on (a, 6] non-uniformly, may have a discontinuous sum as Example 1. Consider a functional series on the segment | 0,1). Let us calculate its n-th partial sum. Therefore, It is discontinuous on a segment, although the terms of the series are continuous on it. By virtue of the proved theorem, this series is not uniformly convergent on an interval. Example 2. Consider the series As shown above, this series converges for, the series will converge uniformly according to the Weierstrass criterion, since 1 and the number series converge. Therefore, for any x> 1, the sum of this series is continuous. Comment. The function is called the Rome function on (this function plays an important role in number theory). Theorem 4 (on term-by-term integration of a functional series). Suppose that all terms fn (x) of the series are continuous and the series converges uniformly on the interval [a, b] to the function S (x). Then the equality holds. By the continuity of the functions fn (x) and the uniform convergence of this series on the interval [a, 6], its sum S (x) is continuous and, therefore, integrable on. Consider the difference From the uniform convergence of the series on [o, b] it follows that for any e> 0 there is a number N (e)> 0 such that for all numbers n> N (e) and for all x ∈ [a, 6] If the series fn (0 is not uniformly convergent, then, generally speaking, it cannot be integrated term-by-term, i.e., Theorem 5 (on term-by-term differentiation of a functional series) Let all terms of the converging series 00 have continuous derivatives and a series composed of of these derivatives, converges uniformly on the interval [a, b]. Then at any point the equality holds, that is, the given series can be differentiated term by term. Let us take any two points. Then, by Theorem 4, we have the function o- (x) is continuous as the sum of a uniformly converging series of continuous functions.Therefore, differentiating the equality, we obtain Exercises Find the regions of convergence of these functional series: Using the Weierstrass test, prove the uniform convergence of these functional series on the indicated intervals:

Topic 2. Functional series. Power series

2.1. Functional ranks

So far, we have considered the series of which numbers were members. Let us now turn to the study of the series, the members of which are functions.

Functional range called a series

whose members are functions of the same argument defined on one set E.

For example,

1.
;

2.
;

Given the argument NS some numerical value
,
, then we get a number series

which can converge (converge absolutely) or diverge.

If at
the resulting number series converges, then the point
calledconvergence point functional range. The collection of all points of convergence is calledconvergence domain functional range. We denote the region of convergence NS, obviously,
.

If for numerical positive series the question is posed: "Does the row converge or diverge?" under what NS?».

Functional range
establishes the law according to which each value of the argument
,
, a number equal to the sum of a number series is put into correspondence
... Thus, on the set NS the function is set
, which is called the sum of the functional series.

Example 16.

Find the region of convergence of a functional series

.

Solution.

Let be NS- a fixed number, then this series can be considered as a numerical series, sign-positive at
and alternating at
.

Let's compose a series of the absolute values ​​of the members of this series:

i.e. for any value NS this limit is less than one, which means that this series converges, and absolutely (since a series of absolute values ​​of the members of the series was investigated) on the entire numerical axis.

Thus, the domain of absolute convergence is the set
.

Example 17.

Find the region of convergence of a functional series
.

Solution.

Let be NS- fixed number,
, then this series can be considered as a numerical series, sign-positive at
and alternating at
.

Consider a series of absolute values ​​of the members of this series:

and apply the DAlembert sign to it.

On the basis of DAlembert, the series converges if the value of the limit is less than one, i.e. this series will converge if
.

Having solved this inequality, we get:


.

Thus, for, the series composed of the absolute values ​​of the members of this series converges, which means that the original series converges absolutely, and for
this series diverges.

At
the series can converge or diverge, since at these values NS the value of the limit is equal to one. Therefore, we additionally investigate the convergence of a series of points
and
.

Substituting into this row
, we get a number series
, about which it is known that it is a harmonic divergent series, which means that the point
- the point of divergence of a given series.

At
an alternating number series is obtained

about which it is known that it converges conditionally (see example 15), which means that the point
- the point of conditional convergence of the series.

Thus, the region of convergence of this series, and the series converges absolutely at.

Functional range

calledmajorized in some region of variation of x, if there is such a converging sign-positive series

,

that for all x from the given region the condition
at
... Row
calledmajorant.

In other words, a series is majorized if each of its terms in absolute value is not greater than the corresponding term of some converging sign-positive series.

For example, the series

is majorized for any NS since for everyone NS the relation holds

at
,

and a number is known to be convergent.

TheoremWeierstrass

A series dominated in a certain area absolutely converges in this area.

Consider, for example, a functional series
... This series is dominated at
since at
the members of the series do not exceed the corresponding members of the positive series ... Consequently, by the Weierstrass theorem, the considered functional series converges absolutely for
.

2.2. Power series. Abel's theorem. Convergence domain of a power series

Among all the variety of functional series, the most important from the point of view of practical application are power and trigonometric series. Let's consider such rows in more detail.

Power series by degrees
is called a functional series of the form

where - some fixed number,
- numbers called the coefficients of the series.

At
we obtain a power series in powers NS which has the form

.

For simplicity, we will consider power series in powers NS, since from such a series it is easy to obtain a series in powers
substituting instead NS expression
.

The simplicity and importance of the class of power series are primarily due to the fact that the partial sum of the power series

is a polynomial - a function whose properties are well studied and whose values ​​are easily calculated using only arithmetic operations.

Since power series are a special case of a functional series, it is also necessary to find the convergence region for them. Unlike the region of convergence of an arbitrary functional series, which can be a set of arbitrary form, the region of convergence of a power series has a well-defined form. This is indicated by the following theorem.

TheoremAbel.

If the power series
converges at some value
, then it converges, and absolutely, for all values ​​of x satisfying the condition
... If the power series diverges at some value
, then it diverges for values ​​satisfying the condition
.

It follows from Abel's theorem that all points of convergence of a power series in powers NS located from the origin are not further than any of the divergence points. Obviously, the points of convergence fill a certain gap centered at the origin. the theorem on the domain of convergence of a power series is valid.

Theorem.

For any power series
there is a numberR (R>0)such that for all x lying inside the interval
, the series converges absolutely and for all x lying outside the interval
, the series diverges.

NumberRcalledradius of convergence power series, and the interval
– convergence interval power series in powers of x.

Note that the theorem does not say anything about the convergence of the series at the ends of the interval of convergence, i.e. in points
... At these points, different power series behave differently: the series can converge (absolutely or conditionally), or it can diverge. Therefore, the convergence of the series at these points should be checked directly by definition.

In special cases, the radius of convergence of the series can be zero or infinity. If
, then the power series in powers NS converges only at one point
; if
, then the power series converges on the entire number axis.

Note once again that the power series
by degrees
can be reduced to a power series
by replacing
... If the row
converges at
, i.e. for
, then after the reverse replacement we get

 or
.

Thus, the interval of convergence of the power series
has the form
... Point are called center of convergence... For clarity, it is customary to depict the convergence interval on the numerical axis (Figure 1)

Thus, the convergence domain consists of the convergence interval, to which the points can be added
if the series converges at these points. The convergence interval can be found by directly applying the DAlembert criterion or the radical Cauchy criterion to a series composed of the absolute values ​​of the members of a given series.

Example 18.

Find the region of convergence of the series
.

Solution.

This series is a power series in degrees NS, i.e.
... Consider a series made up of the absolute values ​​of the members of this series, and use the d'Alembert test.

The series will converge if the value of the limit is less than 1, i.e.

, where
.

Thus, the interval of convergence of this series
, radius of convergence
.

We investigate the convergence of the series at the ends of the interval, at the points
... Substituting into this row the value
, we get the series

.

The resulting series is a harmonic divergent series, therefore, at the point
the row diverges, so the point
is not included in the region of convergence.

At
we get an alternating series

,

which is conditionally convergent (example 15), therefore, the point
– convergence point (conditional).

Thus, the region of convergence of the series
, and at the point
the series converges conditionally, and at other points - absolutely.

The reasoning used to solve the example can be generalized.

Consider the power series

Let us compose a series of the absolute values ​​of the members of the series and apply the Alamber sign D to it.

If there is a (finite or infinite) limit, then according to the convergence condition for the Alamber attribute D, the series will converge if

,

,

.

Hence, from the definition of the interval and the radius of convergence, we have

Applying the radical Cauchy criterion and reasoning similarly, one can obtain another formula for finding the radius of convergence

Example 19

Solution.

The series is exponential in degrees NS. To find the convergence interval, we calculate the convergence radius using the above formula. For a given series, the formula for the numerical coefficient has the form

, then

Hence,

Because R = , then the series converges (and absolutely) for all values NS, those. convergence region NS (–; +).

Note that it would be possible to find the region of convergence without using formulas, but by directly applying Alambert's test D:

Since the value of the limit does not depend on NS and less than 1, then the series converges for all values NS, those. at NS(-;+).

Example 20

Find the region of convergence of the series

1!(NS+5)+2!(NS + 5) 2 +3!(NS + 5) 3 +... + NS!(NS + 5) NS +...

Solution .

x + 5), those. center of convergence NS 0 = - 5. Numerical coefficient of the series a NS = n!.

Find the radius of convergence of the series

.

Thus, the convergence interval consists of one point - the center of the convergence interval x = - 5.

Example 21

Find the region of convergence of the series
.

Solution.

This series is a power series in powers ( NS–2), those.

center of convergence NS 0 = 2. Note that the series is sign-positive for any fixed NS, since the expression ( NS- 2) raised to the power of 2 NS. Let us apply the radical Cauchy criterion to the series.

The series will converge if the value of the limit is less than 1, i.e.

,
,
,

hence the radius of convergence
, then the convergence integral

,
.

Thus, the series converges absolutely for NS
. Note that the convergence integral is symmetric with respect to the center of convergence NS O = 2.

Let us investigate the convergence of the series at the ends of the convergence interval.

Assuming
, we get a numeric positive series

Let's use the necessary convergence criterion:

therefore, the number series diverges, and the point
is the point of divergence. Note that when calculating the limit, a second remarkable limit was used.

Assuming
, we get the same number series (check it yourself!), so the point
is also not included in the convergence interval.

So, the region of absolute convergence of this series NS
.

2.3. Properties of convergent power series

We know that a finite sum of continuous functions is continuous; the sum of differentiable functions is differentiable, and the derivative of the sum is equal to the sum of the derivatives; the final sum can be integrated term by term.

It turns out that in the general case the properties do not hold for "infinite sums" of functions - functional series.

For example, consider the function series

Obviously, all members of the series are continuous functions. Let us find the region of convergence of this series and its sum. To do this, we find the partial sums of the series

then the sum of the series

Thus, the sum S(NS) of a given series, as the limit of a sequence of partial sums, exists and is finite for NS (-1;1), hence, this interval is the region of convergence of the series. Moreover, its sum is a discontinuous function, since

So, this example shows that in the general case the properties of finite sums have no analogue for infinite sums - series. However, for the special case of functional series - power series - the properties of the sum are similar to those of the finite sums.

- perhaps the complex will not be so difficult;) And the title of this article is also disingenuous - the series, which will be discussed today, are more likely not complex, but "rare earth". However, even part-time students are not insured against them, and therefore, to this, it would seem, additional activity should be taken with the utmost seriousness. After all, after working it out, you will be able to deal with almost any "beast"!

Let's start with the classics of the genre:

Example 1

First, note that this is NOT a power series (I remind you that it looks like)... And, secondly, here the meaning immediately catches the eye, which obviously cannot enter the region of convergence of the series. And this is already a small research success!

But still, how to come to great success? I hasten to please you - such rows can be solved in the same way as power-law- relying on the d'Alembert sign or the radical Cauchy sign!

Solution: the value is not included in the convergence range of the series. This is an essential fact, and it must be noted!

The basic algorithm works in a standard way. Using the d'Alembert test, we find the convergence interval of the series:

The series converges at. Let's lift the module up:

Let's immediately check the “bad” point: the value did not enter the convergence region of the series.

Let us investigate the convergence of the series at the "inner" ends of the intervals:
if then
if then

Both numerical series diverge, since it is not fulfilled necessary convergence criterion.

Answer: area of ​​convergence:

Let's do a little analytical check. Let's substitute some value from the right interval into the function series, for example:
- converges in d'Alembert.

In the case of substitution of values ​​from the left interval, converging series are also obtained:
if, then.

And finally, if, then the series - really diverges.

A couple of simple examples to warm up:

Example 2

Find the region of convergence of a functional series

Example 3

Find the region of convergence of a functional series

Be especially good with the "new" module- he will meet 100,500 times today!

Brief solutions and answers at the end of the lesson.

The algorithms used seem to be universal and reliable, but in reality this is not so - for many functional series they often "slip" or even lead to erroneous conclusions (and I will consider such examples too).

Roughness begins already at the level of interpretation of the results: consider, for example, a series. Here, in the limit, we obtain (check it yourself), and in theory it is necessary to give the answer that the series converges at a single point. However, the point is "overplayed", which means that our "patient" diverges everywhere!

And for a series, the "obvious" solution "according to Cauchy" gives nothing at all:
- for ANY value "x".

And the question arises, what to do? Let's use the method that the main part of the lesson will be devoted to! It can be formulated as follows:

Direct analysis of numerical series at different values

In fact, we have already started doing this in Example 1. First, we examine some specific "x" and the corresponding number series. It begs to take the value:
- the resulting numerical series diverges.

And this immediately prompts the thought: what if the same thing happens at other points?
Let's check a necessary criterion for the convergence of a series for arbitrary values:

The point is accounted for above, for all the other "x" we organize a standard appointment second wonderful limit:

Output: the series diverges along the whole number line

And this solution is the most working option!

In practice, the functional range often has to be compared with generalized harmonic series :

Example 4

Solution: first of all, we deal with scope: in this case, the radical expression must be strictly positive, and, in addition, all members of the series must exist, starting from the 1st. It follows from this that:
... With these values, conditionally converging series are obtained:
etc.

Other "x" are not suitable, so, for example, when we get an illegal case where the first two members of the series do not exist.

This is all good, this is all understandable, but there remains one more important question - how to correctly draw up a decision? I propose a scheme that can be jargonally called "transferring arrows" to numerical series:

Consider arbitrary meaning and investigate the convergence of the number series. Routine Leibniz's sign:

1) This row is alternating.

2) - the members of the series decrease in absolute value. Each next term in the series is less in absolute value than the previous one: hence, the decrease is monotonic.

Conclusion: the series converges on the basis of Leibniz. As already noted, the convergence here is conditional - for the reason that the series - diverges.

Just like that - neatly and correctly! For behind the "alpha" we cleverly hid all the admissible number series.

Answer: the functional series exists and converges conditionally at.

A similar example for a stand-alone solution:

Example 5

Explore the convergence of a functional series

An approximate example of finishing the assignment at the end of the lesson.

So much for your "working hypothesis"! - the functional series converges on the interval!

2) With a symmetric interval, everything is transparent, we consider arbitrary values ​​and we get: - absolutely converging numerical series.

3) And, finally, the "middle". It is also convenient to select two intervals here.

Consider arbitrary value from the interval and we get a number series:

! Again - if difficult , substitute any specific number, for example. However, ... you wanted difficulties =)

For all values ​​of "en" , means:
- thus, by comparison criterion the series converges along with an infinitely decreasing progression.

For all values ​​of "x" from the interval we obtain - absolutely converging numerical series.

All the X's have been examined, the X's are gone!

Answer: area of ​​convergence of the series:

I must say, an unexpected result! And it should also be added that the use of d'Alembert or Cauchy signs here will definitely be misleading!

Direct assessment is the "aerobatics" of mathematical analysis, but this, of course, requires experience, and somewhere even intuition.

Maybe someone will find the way easier? Write! By the way, there are precedents - several times readers have suggested more rational decisions and I published them with pleasure.

Successful landing :)

Example 11

Find the region of convergence of a functional series

My version of the solution is very close.

Additional hardcore can be found at Section VI (Rows) collection of Kuznetsov (Problems 11-13). There are ready-made solutions on the internet, but here I owe you warn- many of them are incomplete, incorrect, or even generally erroneous. And, by the way, this was one of the reasons why this article was born.

Let's summarize the three lessons and organize our toolbox. So:

To find the convergence interval (s) of a functional series, one can use:

1) D'Alembert's sign or Cauchy's sign... And if the row is not sedate- we take great care when analyzing the result obtained by direct substitution of various values.

2) The criterion for the uniform convergence of Weierstrass... Let's not forget!

3) Comparison with typical numerical series- rules in the general case.

Then explore the ends of the found intervals (if needed) and we obtain the region of convergence of the series.

Now you have at your disposal a fairly serious arsenal that will allow you to cope with almost any thematic task.

Wish you success!

Solutions and Answers:

Example 2: Solution: the value is not included in the convergence range of the series.
We use the d'Alembert sign:


The series converges for:

Thus, the intervals of convergence of the functional series are: .
Let us investigate the convergence of the series at the endpoints:
if then ;
if then .
Both numerical series diverge, tk. the required convergence criterion is not fulfilled.

Answer : area of ​​convergence: