Solution of fractionally rational trigonometric equations. Solving trigonometric equations. How to solve trigonometric equations

Solution methods trigonometric equations.

Solving a trigonometric equation consists of two stages: equation transformation to get its simplest view (see above) and solutionobtained simplest trigonometric equation. There are seven basic methods for solving trigonometric equations.

1. Algebraic method.

(variable substitution and substitution method).

2. Factoring.

PRI me R 1. Solve the equation: sin x+ cos x = 1 .

Solution. Move all the terms of the equation to the left:

Sin x+ cos x – 1 = 0 ,

We transform and factorize the expression in

Left side of the equation:

PRI me R 2. Solve the equation: cos 2 x+ sin x Cos x = 1.

SOLUTION cos 2 x+ sin x Cos x– sin 2 x- cos 2 x = 0 ,

Sin x Cos x– sin 2 x = 0 ,

Sin x(Cos x– sin x ) = 0 ,

PRI me R 3. Solve the equation: cos 2 x- cos 8 x+ cos 6 x = 1.

SOLUTION cos 2 x+ cos 6 x= 1 + cos 8 x,

2 cos 4 x cos 2 x= 2 cos² 4 x ,

Cos 4 x · (cos 2 x- cos 4 x) = 0 ,

Cos 4 x 2 sin 3 x Sin x = 0 ,

1). cos 4 x= 0, 2). sin 3 x= 0, 3). sin x = 0 ,

3. Bringing to homogeneous equation. The equation called homogeneous from relationally sin and cos , if all of him members of the same degree with respect to sin and cos same angle... To solve a homogeneous equation, you need: a) move all its members to the left side; b) take all common factors out of brackets; v) equate all factors and parentheses to zero; G) the parentheses equated to zero give homogeneous equation of lesser degree, which should be divided by cos(or sin) in the senior degree; d) solve the resulting algebraic equation with respect totan . sin 2 x+ 4 sin x Cos x+ 5 cos 2 x = 2. SOLUTION. 3sin 2 x+ 4 sin x Cos x+ 5 cos 2 x= 2sin 2 x+ 2cos 2 x , Sin 2 x+ 4 sin x Cos x+ 3 cos 2 x = 0 , Tan 2 x+ 4 tan x + 3 = 0 , from here y 2 + 4y +3 = 0 , The roots of this equation are:y 1 = - 1, y 2 = - 3, hence 1) tan x= –1, 2) tan x = –3,

4. Move to half corner.

Let's consider this method with an example:

EXAMPLE Solve equation: 3 sin x- 5 cos x = 7.

SOLUTION.6 sin ( x/ 2) cos ( x/ 2) - 5 cos ² ( x/ 2) + 5 sin ² ( x/ 2) =

7 sin ² ( x/ 2) + 7 cos ² ( x/ 2) ,

2 sin² ( x/ 2) - 6 sin ( x/ 2) cos ( x/ 2) + 12 cos ² ( x/ 2) = 0 ,

tan ² ( x/ 2) - 3 tan ( x/ 2) + 6 = 0 ,

. . . . . . . . . .

5. Introduction of an auxiliary angle.

Consider an equation of the form:

a sin x + b cos x = c ,

Where a, b, c- coefficients;x- the unknown.

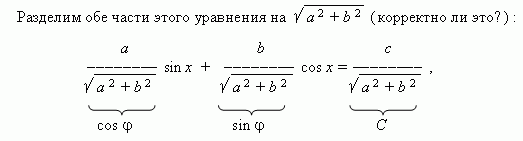
Now the coefficients of the equation have the properties of sine and cosine, namely: modulus (absolute value) of each of which no more than 1, and the sum of their squares is 1. Then we can denote them respectively how cos and sin (here - so-called auxiliary corner), andtake our equation

In this lesson we will look at basic trigonometric functions, their properties and graphs and also list basic types of trigonometric equations and systems... In addition, we indicate general solutions of the simplest trigonometric equations and their special cases.

This lesson will help you prepare for one of the types of assignments. B5 and C1.

Preparation for the exam in mathematics

Experiment

Lesson 10. Trigonometric functions. Trigonometric equations and their systems.

Theory

Lesson summary

We have already used the term "trigonometric function" many times. Even in the first lesson of this topic, we defined them using right triangle and a single trigonometric circle... Using such methods of setting trigonometric functions, we can already conclude that for them exactly one value of the function corresponds to one value of the argument (or angle), i.e. we have the right to call sine, cosine, tangent and cotangent functions.

In this lesson, it's time to try to abstract from the previously considered methods of calculating the values ​​of trigonometric functions. Today we will move on to the usual algebraic approach to working with functions, we will look at their properties and draw graphs.

As for the properties of trigonometric functions, special attention should be paid to:

Domain of definition and range of values, since for sine and cosine there are limits on the range of values, and for tangent and cotangent there are limits on the range of definition;

The periodicity of all trigonometric functions, since we have already noted the presence of the smallest non-zero argument, the addition of which does not change the value of the function. Such an argument is called the period of the function and is denoted by a letter. For sine / cosine and tangent / cotangent, these periods are different.

Consider the function:

1) Scope of definition;

2) Range of values ;

3) The function is odd ;

Let's plot the function. In this case, it is convenient to start plotting from the image of the area, which limits the graph at the top with a number of 1 and at the bottom with a number, which is related to the range of values ​​of the function. In addition, for plotting it is useful to remember the values ​​of the sines of several main table angles, for example, that This will allow you to build the first full "wave" of the chart and then redraw it to the right and left, using the fact that the picture will be repeated with an offset by a period, i.e. on .

Now let's look at the function:

The main properties of this function:

1) Scope of definition;

2) Range of values ;

3) The function is even This implies the symmetry of the graph of the function relative to the ordinate;

4) The function is not monotonic throughout its domain of definition;

Let's plot the function. As in plotting the sine, it is convenient to start with the image of the area that bounds the graph at the top with a number of 1 and at the bottom with a number, which is related to the range of values ​​of the function. We will also plot the coordinates of several points on the graph, for which it is necessary to remember the values ​​of the cosines of several basic table angles, for example, that with the help of these points we can build the first full "wave" of the graph and then redraw it to the right and left, using the fact that the picture will be repeated with a period offset, i.e. on .

Let's move on to the function:

The main properties of this function:

1) Domain of definition except, where. We have already pointed out in previous lessons that does not exist. This statement can be generalized taking into account the period of the tangent;

2) Range of values, i.e. tangent values ​​are not limited;

3) The function is odd ;

4) The function monotonically increases within its so-called branches of the tangent, which we will now see in the figure;

5) The function is periodic with a period

Let's plot the function. In this case, it is convenient to start plotting from the image of the vertical asymptotes of the graph at points that are not included in the domain of definition, i.e. etc. Next, we depict the branches of the tangent inside each of the stripes formed by the asymptotes, pressing them to the left asymptote and to the right. At the same time, do not forget that each branch increases monotonically. We represent all branches in the same way, because the function has a period equal to. This can be seen from the fact that each branch is obtained by displacing the adjacent one along the abscissa axis.

And we conclude by examining the function:

The main properties of this function:

1) Domain of definition except, where. From the table of values ​​of trigonometric functions, we already know that it does not exist. This statement can be generalized considering the cotangent period;

2) Range of values, i.e. cotangent values ​​are not limited;

3) The function is odd ;

4) The function decreases monotonically within its branches, which are similar to the branches of the tangent;

5) The function is periodic with a period

Let's plot the function. In this case, as for the tangent, it is convenient to start plotting from the image of the vertical asymptotes of the graph at points that are not included in the domain of definition, i.e. etc. Next, we depict the branches of the cotangent inside each of the stripes formed by the asymptotes, pressing them to the left asymptote and to the right. In this case, we take into account that each branch decreases monotonically. All branches, similarly to the tangent, are depicted in the same way, since the function has a period equal to.

Separately, it should be noted that trigonometric functions with a complex argument may have a non-standard period. We are talking about functions of the form:

Their period is equal. And about the functions:

Their period is equal.

As you can see, to calculate the new period, the standard period is simply multiplied by the argument. It does not depend on other modifications of the function.

You can learn more about and understand where these formulas come from in the lesson about plotting and transforming function graphs.

We have come to one of the most important parts of the topic "Trigonometry", which we will devote to solving trigonometric equations. The ability to solve such equations is important, for example, when describing oscillatory processes in physics. Imagine that you have driven a few laps in a kart in a sports car, solving a trigonometric equation will help determine how long you have already been in the race, depending on the position of the car on the track.

Let's write down the simplest trigonometric equation:

The solution to such an equation is the arguments, the sine of which is equal to. But we already know that because of the periodicity of the sine, there are an infinite number of such arguments. Thus, the solution to this equation will be, etc. The same applies to the solution of any other simplest trigonometric equation, there will be an infinite number of them.

Trigonometric equations are divided into several basic types. Separately, we should dwell on the simplest, tk. all the rest boil down to them. There are four such equations (according to the number of basic trigonometric functions). General solutions are known for them, they must be remembered.

The simplest trigonometric equations and their general solutions look like this:

Please note that we must take into account the known limitations on the values ​​of sine and cosine. If, for example,, then the equation has no solutions and the indicated formula should not be applied.

In addition, the specified root formulas contain a parameter in the form of an arbitrary integer. V school curriculum this is the only case when a solution to an equation without a parameter contains a parameter. This arbitrary integer shows that it is possible to write out an infinite number of roots of any of the above equations simply by substituting all integers in turn instead.

You can get acquainted with the detailed receipt of these formulas by repeating the chapter "Trigonometric Equations" in the 10th grade algebra program.

Separately, it is necessary to pay attention to the solution of particular cases of the simplest equations with sine and cosine. These equations are:

General solution formulas should not be applied to them. Such equations are most conveniently solved using a trigonometric circle, which gives a simpler result than formulas for general solutions.

For example, the solution to the equation is ... Try to get this answer yourself and solve the rest of the above equations.

In addition to the indicated most common type of trigonometric equations, there are several more standard ones. Let's list them taking into account those that we have already indicated:

1) The simplest, for example, ;

2) Particular cases of the simplest equations, for example, ;

3) Complex Argument Equations, for example, ;

4) Equations Reducing to the Simplest Way of Taking a Common Factor, for example, ;

5) Equations that reduce to the simplest way by transforming trigonometric functions, for example, ;

6) Equations Reducing to the Simplest Using Substitution, for example, ;

7) Homogeneous equations, for example, ;

8) Equations Solved Using Function Properties, for example, ... Do not be afraid that there are two variables in this equation, it is being solved at the same time;

As well as equations that are solved using various methods.

In addition to solving trigonometric equations, you must be able to solve their systems.

The most common systems of the following types:

1) In which one of the equations is the power, for example, ;

2) Systems of the simplest trigonometric equations, for example, .

In today's lesson, we looked at the basic trigonometric functions, their properties and graphs. And also got acquainted with the general formulas for solving the simplest trigonometric equations, indicated the main types of such equations and their systems.

In the practical part of the lesson, we will analyze methods for solving trigonometric equations and their systems.

Box 1.Solving particular cases of the simplest trigonometric equations.

As we already said in the main part of the lesson, special cases of trigonometric equations with sine and cosine of the form:

have more simple solutions than the formulas for general solutions give.

For this, a trigonometric circle is used. Let us analyze the method for solving them using the example of an equation.

Let's draw on the trigonometric circle the point at which the cosine value is equal to zero, it is also the coordinate along the abscissa axis. As you can see, there are two such points. Our task is to indicate what is the angle that corresponds to these points on the circle.

We start counting from the positive direction of the abscissa axis (cosine axis) and, when plotting the angle, we get to the first depicted point, i.e. one solution would be this angle value. But we are still satisfied with the angle that corresponds to the second point. How to get into it?

Examples:

\ (2 \ sin (⁡x) = \ sqrt (3) \)
tg \ ((3x) = - \) \ (\ frac (1) (\ sqrt (3)) \)
\ (4 \ cos ^ 2⁡x + 4 \ sin⁡x-1 = 0 \)
\ (\ cos⁡4x + 3 \ cos⁡2x = 1 \)

How to solve trigonometric equations:

Any trigonometric equation should be reduced to one of the following types:

\ (\ sin⁡t = a \), \ (\ cos⁡t = a \), tg \ (t = a \), ctg \ (t = a \)

where \ (t \) is an expression with an x, \ (a \) is a number. Such trigonometric equations are called the simplest... They can be easily solved using () or special formulas:

For an infographic on solving the simplest trigonometric equations, see here:, and.

Example ... Solve the trigonometric equation \ (\ sin⁡x = - \) \ (\ frac (1) (2) \).
Solution:

Answer: \ (\ left [\ begin (gathered) x = - \ frac (π) (6) + 2πk, \\ x = - \ frac (5π) (6) + 2πn, \ end (gathered) \ right. \) \ (k, n∈Z \)

For what each symbol in the formula for the roots of trigonometric equations means, see.

Attention! The equations \ (\ sin⁡x = a \) and \ (\ cos⁡x = a \) have no solutions if \ (a ϵ (-∞; -1) ∪ (1; ∞) \). Because the sine and cosine for any x is greater than or equal to \ (- 1 \) and less than or equal to \ (1 \):

\ (- 1≤ \ sin x≤1 \) \ (- 1≤ \ cos⁡x≤1 \)

Example ... Solve the equation \ (\ cos⁡x = -1,1 \).
Solution: \(-1,1<-1\), а значение косинуса не может быть меньше \(-1\). Значит у уравнения нет решения.
Answer : no solutions.

Example ... Solve the trigonometric equation tg \ (⁡x = 1 \).
Solution:

Let's solve the equation using the number circle. For this: 1) Construct a circle) 2) Construct the axes \ (x \) and \ (y \) and the tangent axis (it passes through the point \ ((0; 1) \) parallel to the \ (y \) axis). 3) On the tangent axis, mark the point \ (1 \). 4) Let's connect this point and the origin - a straight line. 5) Let's mark the points of intersection of this line and the number circle. 6) Let's sign the values ​​of these points: \ (\ frac (π) (4) \), \ (\ frac (5π) (4) \) 7) Let's write down all the values ​​of these points. Since they are at a distance of exactly \ (π \) from each other, all values ​​can be written in one formula:

Answer: \ (x = \) \ (\ frac (π) (4) \) \ (+ πk \), \ (k∈Z \).

Example ... Solve the trigonometric equation \ (\ cos⁡ (3x + \ frac (π) (4)) = 0 \).
Solution:

Let's use the number circle again. 1) Construct a circle, axes \ (x \) and \ (y \). 2) On the cosine axis (axis \ (x \)) we mark \ (0 \). 3) Let's draw a perpendicular to the cosine axis through this point. 4) Let's mark the points of intersection of the perpendicular and the circle. 5) Let's sign the values ​​of these points: \ (- \) \ (\ frac (π) (2) \), \ (\ frac (π) (2) \). 6) Let's write out all the value of these points and equate them to the cosine (to what is inside the cosine). \ (3x + \) \ (\ frac (π) (4) \) \ (= ± \) \ (\ frac (π) (2) \) \ (+ 2πk \), \ (k∈Z \) \ (3x + \) \ (\ frac (π) (4) \) \ (= \) \ (\ frac (π) (2) \) \ (+ 2πk \) \ (3x + \) \ (\ frac ( π) (4) \) \ (= - \) \ (\ frac (π) (2) \) \ (+ 2πk \) 8) As usual, we will express \ (x \) in the equations. Do not forget to treat numbers with \ (π \), as well as \ (1 \), \ (2 \), \ (\ frac (1) (4) \), etc. These are the same numbers as everyone else. No numerical discrimination! \ (3x = - \) \ (\ frac (π) (4) \) \ (+ \) \ (\ frac (π) (2) \) \ (+ 2πk \) \ (3x = - \) \ (\ frac (π) (4) \) \ (+ \) \ (\ frac (π) (2) \) \ (+ 2πk \) \ (3x = \) \ (\ frac (π) (4) \) \ (+ 2πk \) \ (|: 3 \) \ (3x = - \) \ (\ frac (3π) (4) \) \ (+ 2πk \) \ (|: 3 \) \ (x = \) \ (\ frac (π) (12) \) \ (+ \) \ (\ frac (2πk) (3) \) \ (x = - \) \ (\ frac (π) ( 4) \) \ (+ \) \ (\ frac (2πk) (3) \)

Answer: \ (x = \) \ (\ frac (π) (12) \) \ (+ \) \ (\ frac (2πk) (3) \) \ (x = - \) \ (\ frac (π) ( 4) \) \ (+ \) \ (\ frac (2πk) (3) \), \ (k∈Z \).

Reducing trigonometric equations to the simplest is a creative task, here you need to use and, and special methods for solving equations:
- Method (the most popular in the exam).
- Method.
- Method of auxiliary arguments.

Consider an example of solving the square-trigonometric equation

Example ... Solve the trigonometric equation \ (2 \ cos ^ 2⁡x-5 \ cos⁡x + 2 = 0 \)
Solution:

\ (2 \ cos ^ 2⁡x-5 \ cos⁡x + 2 = 0 \)	Let's make the replacement \ (t = \ cos⁡x \).
	Our equation has become typical. You can solve it with.
\ (D = 25-4 \ cdot 2 \ cdot 2 = 25-16 = 9 \)
\ (t_1 = \) \ (\ frac (5-3) (4) \) \ (= \) \ (\ frac (1) (2) \); \ (t_2 = \) \ (\ frac (5 + 3) (4) \) \ (= 2 \)	We do the reverse replacement.
\ (\ cos⁡x = \) \ (\ frac (1) (2) \); \ (\ cos⁡x = 2 \)	Solve the first equation using the number circle. The second equation has no solutions because \ (\ cos⁡x∈ [-1; 1] \) and cannot be equal to two for any x.
	Let's write down all the numbers lying on at these points.

Answer: \ (x = ± \) \ (\ frac (π) (3) \) \ (+ 2πk \), \ (k∈Z \).

An example of solving a trigonometric equation with the study of ODZ:

Example (exam) ... Solve the trigonometric equation \ (= 0 \)

\ (\ frac (2 \ cos ^ 2⁡x- \ sin (⁡2x)) (ctg x) \)\(=0\)	If there is a fraction and there is a cotangent, then you need to write it down. Let me remind you that the cotangent is actually a fraction: ctg \ (x = \) \ (\ frac (\ cos⁡x) (\ sin⁡x) \) Therefore, ODZ for ctg \ (x \): \ (\ sin⁡x ≠ 0 \).
ODZ: ctg \ (x ≠ 0 \); \ (\ sin⁡x ≠ 0 \) \ (x ≠ ± \) \ (\ frac (π) (2) \) \ (+ 2πk \); \ (x ≠ πn \); \ (k, n∈Z \)	Let's mark the “non-solutions” on the number circle.
\ (\ frac (2 \ cos ^ 2⁡x- \ sin (⁡2x)) (ctg x) \)\(=0\)	Let's get rid of the denominator in the equation by multiplying it by ctg \ (x \). We can do this, since we wrote above that ctg \ (x ≠ 0 \).
\ (2 \ cos ^ 2⁡x- \ sin⁡ (2x) = 0 \)	Apply the double angle sine formula: \ (\ sin⁡ (2x) = 2 \ sin⁡x \ cos⁡x \).
\ (2 \ cos ^ 2⁡x-2 \ sin⁡x \ cos⁡x = 0 \)	If your hands are stretched out to divide by cosine - pull them back! You can divide by an expression with a variable if it is not exactly zero (for example, such as \ (x ^ 2 + 1.5 ^ x \)). Instead, put \ (\ cos⁡x \) outside the parentheses.
\ (\ cos⁡x (2 \ cos⁡x-2 \ sin⁡x) = 0 \)	Let's "split" the equation into two.
\ (\ cos⁡x = 0 \); \ (2 \ cos⁡x-2 \ sin⁡x = 0 \)	Solve the first equation with a number circle. Divide the second equation by \ (2 \) and move \ (\ sin⁡x \) to the right side.
\ (x = ± \) \ (\ frac (π) (2) \) \ (+ 2πk \), \ (k∈Z \). \ (\ cos⁡x = \ sin⁡x \)	The roots that turned out are not included in the LDZ. Therefore, we will not write them down in response. The second equation is typical. Divide it by \ (\ sin⁡x \) (\ (\ sin⁡x = 0 \) cannot be a solution to the equation, since in this case \ (\ cos⁡x = 1 \) or \ (\ cos⁡ x = -1 \)).
	Use the circle again.
\ (x = \) \ (\ frac (π) (4) \) \ (+ πn \), \ (n∈Z \)	These roots are not excluded by the ODZ, so you can write them in response.

Answer: \ (x = \) \ (\ frac (π) (4) \) \ (+ πn \), \ (n∈Z \).

Class: 10

"Equations will last forever."

A. Einstein

Lesson objectives:

• Educational:
  • deepening understanding of methods for solving trigonometric equations;
  • develop skills to distinguish, correctly select ways to solve trigonometric equations.
• Educational:
  • fostering cognitive interest in the educational process;
  • the formation of the ability to analyze the task;
  • contribute to the improvement of the psychological climate in the classroom.
• Developing:
  • contribute to the development of the skill of independent acquisition of knowledge;
  • promote the ability of students to argue their point of view;

Equipment: poster with basic trigonometric formulas, computer, projector, screen.

1 lesson

I. Updating basic knowledge

Solve the equations orally:

1) cosx = 1;
2) 2 cosx = 1;
3) cosx = -;
4) sin2x = 0;
5) sinx = -;
6) sinx =;
7) tgx =;
8) cos 2 x - sin 2 x = 0

1) x = 2k;
2) x = ± + 2k;
3) x = ± + 2k;
4) x = k;
5) x = (–1) + k;
6) x = (–1) + 2k;
7) x = + k;
8) x = + k; to Z.

II. Learning new material

- Today we will consider more complex trigonometric equations. Let's consider 10 ways to solve them. Next there will be two lessons to consolidate, and the next lesson will be a test work. At the stand "To the lesson" posted tasks, similar to which will be on the test work, you need to solve them before the test work. (The day before, before testing, post the solutions of these tasks on the stand).

So, let's move on to considering ways to solve trigonometric equations. Some of these methods will probably seem difficult to you, while others - easy, because you already know some of the techniques for solving equations.

Four students in the class received an individual assignment: to understand and show you 4 ways to solve trigonometric equations.

(The presenters have prepared slides in advance. The rest of the class will write the main steps for solving the equations in a notebook.)

1 student: 1 way. Solving Equations by Factoring

sin 4x = 3 cos 2x

To solve the equation, we use the formula for the sine of a double angle sin 2 = 2 sin cos
2 sin 2x cos 2x - 3 cos 2x = 0,
cos 2x (2 sin 2x - 3) = 0. The product of these factors is zero if at least one of the factors is zero.

2x = + k, k Z or sin 2x = 1.5 - there are no solutions, because | sin | 1
x = + k; to Z.
Answer: x = + k, k Z.

2 student. Method 2. Solving equations by converting the sum or difference of trigonometric functions into a product

cos 3x + sin 2x - sin 4x = 0.

To solve the equation, we use the formula sin– sin = 2 sin сos

cos 3x + 2 sin сos = 0,

cos 3x - 2 sin x cos 3x = 0,

cos 3x (1 - 2 sinx) = 0. The resulting equation is equivalent to a combination of two equations:

The set of solutions to the second equation is completely included in the set of solutions to the first equation. Means

Answer:

3 student. Method 3. Solving equations by transforming the product of trigonometric functions into a sum

sin 5x cos 3x = sin 6x cos2x.

To solve the equation, we use the formula

Answer:

4 student. Method 4. Solving equations that reduce to quadratic equations

3 sin x - 2 cos 2 x = 0,
3 sin x - 2 (1 - sin 2 x) = 0,
2 sin 2 x + 3 sin x - 2 = 0,

Let sin x = t, where | t |. We get the quadratic equation 2t 2 + 3t - 2 = 0,

D = 9 + 16 = 25.

Thus . does not satisfy the condition | t |.

Hence sin x =. That's why .

Answer:

III. Consolidation of what was learned from the textbook by A.N. Kolmogorov

1.No. 164 (a), 167 (a) (quadratic equation)
2.No. 168 (a) (factorization)
3.No. 174 (a) (sum to product conversion)
4. (product to sum conversion)

(At the end of the lesson, show the solution of these equations on the screen for verification)

№ 164 (a)

2 sin 2 x + sin x - 1 = 0.
Let sin x = t, | t | 1. Then
2 t 2 + t - 1 = 0, t = - 1, t =. Where

Answer: - .

№ 167 (a)

3 tg 2 x + 2 tg x - 1 = 0.

Let tg x = 1, then we get the equation 3 t 2 + 2 t - 1 = 0.

Answer:

№ 168 (a)

Answer:

№ 174 (a)

Solve the equation:

Answer:

2 lesson (lesson-lecture)

IV. Learning new material(continuation)

- So, we will continue to study ways to solve trigonometric equations.

Method 5. Solving homogeneous trigonometric equations

Equations of the form a sin x + b cos x = 0, where a and b are some numbers, are called homogeneous equations of the first degree with respect to sin x or cos x.

Consider the equation

sin x - cos x = 0... Divide both sides of the equation by cos x. This can be done, there will be no root loss, because , if cos x = 0, then sin x = 0... But this contradicts the basic trigonometric identity sin 2 x + cos 2 x = 1.

We get tg x - 1 = 0.

tg x = 1,

Equations of the form a sin 2 x + bcos 2 x + c sin x cos x = 0, where a, b, c - some numbers are called homogeneous equations of the second degree with respect to sin x or cos x.

Consider the equation

sin 2 x - 3 sin x cos x + 2 cos 2 = 0. Divide both sides of the equation by cos x, and there will be no root loss, since cos x = 0 is not the root of this equation.

tg 2 x - 3tg x + 2 = 0.

Let tg x = t. D = 9 - 8 = 1.

Then Hence tg x = 2 or tg x = 1.

As a result, x = arctan 2 +, x =

Answer: arctg 2 +,

Consider another equation: 3 sin 2 x - 3 sin x cos x + 4 cos 2 x = 2.
Rewrite the right side of the equation as 2 = 2 1 = 2 (sin 2 x + cos 2 x). Then we get:
3sin 2 x - 3sin x cos x + 4cos 2 x = 2 (sin 2 x + cos 2 x),
3sin 2 x - 3sin x cos x + 4cos 2 x - 2sin 2 x - 2 cos 2 x = 0,
sin 2 x - 3sin x cos x + 2cos 2 x = 0. (Received 2 equation, which has already been analyzed).

Answer: arctg 2 + k,

Method 6. Solving linear trigonometric equations

A linear trigonometric equation is an equation of the form a sin x + b cos x = c, where a, b, c are some numbers.

Consider the equation sin x + cos x= – 1.
Let's rewrite the equation as:

Considering that and, we get:

Answer:

Method 7. Introducing an additional argument

Expression a cos x + b sin x can be converted:

(we have already used this transformation when simplifying trigonometric expressions)

Let's introduce an additional argument - an angle such that

Then

Consider the equation: 3 sinx + 4 cosx = 1. =

Homework: No. 164 -170 (c, d).

The concept of solving trigonometric equations.

• To solve a trigonometric equation, convert it to one or more basic trigonometric equations. Solving a trigonometric equation ultimately comes down to solving four basic trigonometric equations.

Solving basic trigonometric equations.

• There are 4 types of basic trigonometric equations:
• sin x = a; cos x = a
• tg x = a; ctg x = a
• Solving basic trigonometric equations involves looking at the different x positions on the unit circle and using a conversion table (or calculator).
• Example 1.sin x = 0.866. Using a conversion table (or calculator), you get the answer: x = π / 3. The unit circle gives another answer: 2π / 3. Remember: all trigonometric functions are periodic, that is, their values ​​are repeated. For example, the periodicity of sin x and cos x is 2πn, and the periodicity of tg x and ctg x is πn. Therefore, the answer is written as follows:
• x1 = π / 3 + 2πn; x2 = 2π / 3 + 2πn.
• Example 2.cos x = -1/2. Using a conversion table (or calculator), you get the answer: x = 2π / 3. The unit circle gives another answer: -2π / 3.
• x1 = 2π / 3 + 2π; x2 = -2π / 3 + 2π.
• Example 3.tg (x - π / 4) = 0.
• Answer: x = π / 4 + πn.
• Example 4. ctg 2x = 1.732.
• Answer: x = π / 12 + πn.

Transformations used to solve trigonometric equations.

• To transform trigonometric equations, algebraic transformations (factorization, reduction of homogeneous terms, etc.) and trigonometric identities are used.
• Example 5. Using trigonometric identities, the equation sin x + sin 2x + sin 3x = 0 is transformed into the equation 4cos x * sin (3x / 2) * cos (x / 2) = 0. Thus, you need to solve the following basic trigonometric equations: cos x = 0; sin (3x / 2) = 0; cos (x / 2) = 0.

• Finding angles from known values ​​of functions.

  • Before learning methods for solving trigonometric equations, you need to learn how to find angles from known values ​​of functions. This can be done using a conversion table or calculator.
  • Example: cos x = 0.732. The calculator will give the answer x = 42.95 degrees. The unit circle will give additional angles, the cosine of which is also 0.732.

• Set the solution aside on the unit circle.

  • You can defer the solutions to the trigonometric equation on the unit circle. The solutions of the trigonometric equation on the unit circle represent the vertices of a regular polygon.
  • Example: The solutions x = π / 3 + πn / 2 on the unit circle are the vertices of a square.
  • Example: The solutions x = π / 4 + πn / 3 on the unit circle represent the vertices of a regular hexagon.

• Methods for solving trigonometric equations.

  • If a given trig equation contains only one trig function, solve that equation as the basic trig equation. If a given equation includes two or more trigonometric functions, then there are 2 methods for solving such an equation (depending on the possibility of its transformation).
    • Method 1.
  • Convert this equation to an equation of the form: f (x) * g (x) * h (x) = 0, where f (x), g (x), h (x) are the basic trigonometric equations.
  • Example 6.2cos x + sin 2x = 0. (0< x < 2π)
  • Solution. Using the double angle formula sin 2x = 2 * sin x * cos x, replace sin 2x.
  • 2cos x + 2 * sin x * cos x = 2cos x * (sin x + 1) = 0. Now solve the two basic trigonometric equations: cos x = 0 and (sin x + 1) = 0.
  • Example 7.cos x + cos 2x + cos 3x = 0. (0< x < 2π)
  • Solution: Using trigonometric identities, transform this equation into an equation of the form: cos 2x (2cos x + 1) = 0. Now solve the two basic trigonometric equations: cos 2x = 0 and (2cos x + 1) = 0.
  • Example 8.sin x - sin 3x = cos 2x. (0< x < 2π)
  • Solution: Using trigonometric identities, transform this equation into an equation of the form: -cos 2x * (2sin x + 1) = 0. Now solve the two basic trigonometric equations: cos 2x = 0 and (2sin x + 1) = 0.
    • Method 2.
  • Convert the given trigonometric equation to an equation containing only one trigonometric function. Then replace this trigonometric function with some unknown, for example, t (sin x = t; cos x = t; cos 2x = t, tg x = t; tg (x / 2) = t, etc.).
  • Example 9.3sin ^ 2 x - 2cos ^ 2 x = 4sin x + 7 (0< x < 2π).
  • Solution. In this equation, replace (cos ^ 2 x) with (1 - sin ^ 2 x) (by identity). The transformed equation is:
  • 3sin ^ 2 x - 2 + 2sin ^ 2 x - 4sin x - 7 = 0. Replace sin x with t. The equation now looks like this: 5t ^ 2 - 4t - 9 = 0. This is a quadratic equation with two roots: t1 = -1 and t2 = 9/5. The second root t2 does not satisfy the range of values ​​of the function (-1< sin x < 1). Теперь решите: t = sin х = -1; х = 3π/2.
  • Example 10.tg x + 2 tg ^ 2 x = ctg x + 2
  • Solution. Replace tg x with t. Rewrite the original equation as follows: (2t + 1) (t ^ 2 - 1) = 0. Now find t and then find x for t = tg x.

• Special trigonometric equations.

  • There are several special trigonometric equations that require specific transformations. Examples:
  • a * sin x + b * cos x = c; a (sin x + cos x) + b * cos x * sin x = c;
  • a * sin ^ 2 x + b * sin x * cos x + c * cos ^ 2 x = 0

• Periodicity of trigonometric functions.

  • As mentioned earlier, all trigonometric functions are periodic, that is, their values ​​are repeated after a certain period. Examples:
    • The period of the function f (x) = sin x is 2π.
    • The period of the function f (x) = tan x is equal to π.
    • The period of the function f (x) = sin 2x is π.
    • The period of the function f (x) = cos (x / 2) is 4π.
  • If the period is specified in the problem, calculate the value of "x" within this period.
  • Note: Solving trigonometric equations is not an easy task and often leads to errors. So check your answers carefully. To do this, you can use a graphing calculator to plot the given equation R (x) = 0. In such cases, solutions will be presented as decimal fractions (that is, π is replaced by 3.14).