சமன்பாட்டை படிகளில் தீர்க்கவும். இணையத்தில் பின்னங்களுடன் சமன்பாட்டைத் தீர்க்கவும். எளிய நேரியல் சமன்பாடுகளின் உண்மையான எடுத்துக்காட்டுகளைத் தீர்ப்பது

இந்த வீடியோவில், ஒரே அல்காரிதத்தைப் பயன்படுத்தி தீர்க்கப்படும் நேரியல் சமன்பாடுகளின் முழு தொகுப்பையும் பகுப்பாய்வு செய்வோம் - அதனால்தான் அவை எளிமையானவை என்று அழைக்கப்படுகின்றன.

தொடங்குவதற்கு, வரையறுப்போம்: நேரியல் சமன்பாடு என்றால் என்ன, அவற்றில் எது எளிமையானது என்று அழைக்கப்பட வேண்டும்?

ஒரு நேரியல் சமன்பாடு என்பது ஒரே ஒரு மாறி மட்டுமே இருக்கும் மற்றும் முதல் பட்டத்தில் மட்டுமே உள்ளது.

எளிமையான சமன்பாடு என்பது கட்டுமானத்தைக் குறிக்கிறது:

மற்ற அனைத்து நேரியல் சமன்பாடுகளும் அல்காரிதத்தைப் பயன்படுத்தி எளிமையானவையாகக் குறைக்கப்படுகின்றன:

1. திறந்த அடைப்புக்குறிகள், ஏதேனும் இருந்தால்;
2. மாறி உள்ள சொற்களை சம அடையாளத்தின் ஒரு பக்கத்திற்கும், மாறி இல்லாத விதிமுறைகளை மற்றொன்றுக்கும் நகர்த்தவும்;
3. சம அடையாளத்தின் இடது மற்றும் வலது பக்கம் ஒத்த சொற்களைக் கொண்டு வாருங்கள்;
4. இதன் விளைவாக வரும் சமன்பாட்டை $x$ மாறியின் குணகத்தால் வகுக்கவும்.

நிச்சயமாக, இந்த அல்காரிதம் எப்போதும் உதவாது. உண்மை என்னவென்றால், சில நேரங்களில், இந்த அனைத்து சூழ்ச்சிகளுக்கும் பிறகு, $x$ மாறியின் குணகம் பூஜ்ஜியத்திற்கு சமமாக மாறும். இந்த வழக்கில், இரண்டு விருப்பங்கள் சாத்தியமாகும்:

1. சமன்பாட்டில் தீர்வுகள் எதுவும் இல்லை. எடுத்துக்காட்டாக, நீங்கள் $0\cdot x=8$ போன்ற ஒன்றைப் பெறும்போது, ​​அதாவது. இடதுபுறத்தில் பூஜ்ஜியம், வலதுபுறம் பூஜ்ஜியம் அல்லாத எண். கீழேயுள்ள வீடியோவில், இந்த நிலைமை ஏன் சாத்தியமாகிறது என்பதற்கான பல காரணங்களைப் பார்ப்போம்.
2. தீர்வு அனைத்து எண்கள். சமன்பாடு $0\cdot x=0$ என குறைக்கப்பட்டால் மட்டுமே இது சாத்தியமாகும். நாம் எந்த $x$ ஐ மாற்றினாலும், அது "பூஜ்ஜியம் பூஜ்ஜியத்திற்கு சமம்" என்று மாறிவிடும் என்பது மிகவும் தர்க்கரீதியானது, அதாவது. சரியான எண் சமத்துவம்.

இப்போது உண்மையான சிக்கல்களின் உதாரணத்தில் இவை அனைத்தும் எவ்வாறு செயல்படுகின்றன என்பதைப் பார்ப்போம்.

சமன்பாடுகளைத் தீர்ப்பதற்கான எடுத்துக்காட்டுகள்

இன்று நாம் நேரியல் சமன்பாடுகளைக் கையாளுகிறோம், எளிமையானவை மட்டுமே. பொதுவாக, ஒரு நேரியல் சமன்பாடு என்பது சரியாக ஒரு மாறியைக் கொண்டிருக்கும் எந்த சமத்துவத்தையும் குறிக்கிறது, மேலும் அது முதல் நிலைக்கு மட்டுமே செல்கிறது.

இத்தகைய கட்டுமானங்கள் தோராயமாக அதே வழியில் தீர்க்கப்படுகின்றன:

1. முதலில், நீங்கள் அடைப்புக்குறிகளைத் திறக்க வேண்டும், ஏதேனும் இருந்தால் (எங்கள் கடைசி உதாரணத்தைப் போல);
2. பிறகு இதே போல் கொண்டு வாருங்கள்
3. இறுதியாக, மாறியை தனிமைப்படுத்தவும், அதாவது. மாறியுடன் இணைக்கப்பட்டுள்ள அனைத்தும் - அதில் உள்ள விதிமுறைகள் - ஒரு பக்கத்திற்கு மாற்றப்படும், மேலும் அது இல்லாமல் மீதமுள்ள அனைத்தும் மறுபக்கத்திற்கு மாற்றப்படும்.

பின்னர், ஒரு விதியாக, நீங்கள் விளைந்த சமத்துவத்தின் ஒவ்வொரு பக்கத்திலும் ஒத்ததாக இருக்க வேண்டும், அதன் பிறகு அது "x" இல் உள்ள குணகத்தால் வகுக்க மட்டுமே உள்ளது, மேலும் இறுதி பதிலைப் பெறுவோம்.

கோட்பாட்டில், இது அழகாகவும் எளிமையாகவும் தெரிகிறது, ஆனால் நடைமுறையில், அனுபவம் வாய்ந்த உயர்நிலைப் பள்ளி மாணவர்கள் கூட மிகவும் எளிமையான நேரியல் சமன்பாடுகளில் புண்படுத்தும் தவறுகளைச் செய்யலாம். வழக்கமாக, அடைப்புக்குறிகளைத் திறக்கும்போது அல்லது "பிளஸ்கள்" மற்றும் "மைனஸ்கள்" எண்ணும் போது தவறுகள் செய்யப்படுகின்றன.

கூடுதலாக, ஒரு நேரியல் சமன்பாட்டில் தீர்வுகள் இல்லை, அல்லது தீர்வு முழு எண் கோடாக இருக்கும், அதாவது. எந்த எண். இன்றைய பாடத்தில் இந்த நுணுக்கங்களை பகுப்பாய்வு செய்வோம். ஆனால் நீங்கள் ஏற்கனவே புரிந்து கொண்டபடி, எளிமையான பணிகளுடன் தொடங்குவோம்.

எளிய நேரியல் சமன்பாடுகளைத் தீர்ப்பதற்கான திட்டம்

தொடங்குவதற்கு, எளிமையான நேரியல் சமன்பாடுகளைத் தீர்ப்பதற்கான முழுத் திட்டத்தையும் மீண்டும் ஒருமுறை எழுதுகிறேன்:

1. அடைப்புக்குறிகள் ஏதேனும் இருந்தால் விரிவாக்கவும்.
2. தனித்து மாறிகள், அதாவது. "x" உள்ள அனைத்தும் ஒரு பக்கத்திற்கும், "x" இல்லாமல் - மற்றொன்றுக்கும் மாற்றப்படும்.
3. இதே போன்ற விதிமுறைகளை நாங்கள் முன்வைக்கிறோம்.
4. "x" இல் உள்ள குணகத்தால் எல்லாவற்றையும் வகுக்கிறோம்.

நிச்சயமாக, இந்த திட்டம் எப்போதும் வேலை செய்யாது, இது சில நுணுக்கங்கள் மற்றும் தந்திரங்களைக் கொண்டுள்ளது, இப்போது நாம் அவற்றைப் பற்றி அறிந்து கொள்வோம்.

எளிய நேரியல் சமன்பாடுகளின் உண்மையான எடுத்துக்காட்டுகளைத் தீர்ப்பது

பணி எண் 1

முதல் கட்டத்தில், அடைப்புக்குறிகளைத் திறக்க வேண்டும். ஆனால் அவை இந்த எடுத்துக்காட்டில் இல்லை, எனவே இந்த படிநிலையைத் தவிர்க்கிறோம். இரண்டாவது கட்டத்தில், நாம் மாறிகளை தனிமைப்படுத்த வேண்டும். தயவுசெய்து கவனிக்கவும்: நாங்கள் தனிப்பட்ட விதிமுறைகளைப் பற்றி மட்டுமே பேசுகிறோம். எழுதுவோம்:

இடது மற்றும் வலதுபுறத்தில் ஒத்த சொற்களை நாங்கள் தருகிறோம், ஆனால் இது ஏற்கனவே இங்கே செய்யப்பட்டுள்ளது. எனவே, நாங்கள் நான்காவது படிக்குச் செல்கிறோம்: ஒரு காரணி மூலம் வகுக்கவும்:

\[\frac(6x)(6)=-\frac(72)(6)\]

இதோ விடை கிடைத்தது.

பணி #2

இந்த பணியில், அடைப்புக்குறிகளை நாம் கவனிக்க முடியும், எனவே அவற்றை விரிவாக்குவோம்:

இடது மற்றும் வலதுபுறத்தில், ஏறக்குறைய ஒரே கட்டுமானத்தைப் பார்க்கிறோம், ஆனால் வழிமுறையின்படி செயல்படுவோம், அதாவது. சீக்வெஸ்டர் மாறிகள்:

இது போன்ற சில இங்கே:

இது எந்த வேர்களில் வேலை செய்கிறது? பதில்: எதற்கும். எனவே, $x$ எந்த எண் என்று எழுதலாம்.

பணி #3

மூன்றாவது நேரியல் சமன்பாடு ஏற்கனவே மிகவும் சுவாரஸ்யமானது:

\[\left(6-x \right)+\left(12+x \right)-\left(3-2x \right)=15\]

இங்கே பல அடைப்புக்குறிகள் உள்ளன, ஆனால் அவை எதையும் பெருக்கவில்லை, அவற்றுக்கு முன்னால் வெவ்வேறு அடையாளங்கள் உள்ளன. அவற்றை உடைப்போம்:

எங்களுக்கு ஏற்கனவே தெரிந்த இரண்டாவது படியை நாங்கள் செய்கிறோம்:

\[-x+x+2x=15-6-12+3\]

கணக்கிடுவோம்:

நாங்கள் கடைசி படியைச் செய்கிறோம் - எல்லாவற்றையும் "x" இல் உள்ள குணகத்தால் வகுக்கிறோம்:

\[\frac(2x)(x)=\frac(0)(2)\]

நேரியல் சமன்பாடுகளைத் தீர்க்கும்போது நினைவில் கொள்ள வேண்டியவை

மிகவும் எளிமையான பணிகளை நாம் புறக்கணித்தால், பின்வருவனவற்றைச் சொல்ல விரும்புகிறேன்:

• நான் மேலே கூறியது போல், ஒவ்வொரு நேரியல் சமன்பாட்டிற்கும் ஒரு தீர்வு இல்லை - சில நேரங்களில் வெறுமனே வேர்கள் இல்லை;
• வேர்கள் இருந்தாலும், அவற்றில் பூஜ்ஜியம் நுழையலாம் - அதில் தவறில்லை.

பூஜ்ஜியம் மற்ற எண்களைப் போலவே உள்ளது, நீங்கள் அதை எப்படியாவது பாகுபடுத்தக்கூடாது அல்லது பூஜ்ஜியத்தைப் பெற்றால், நீங்கள் ஏதாவது தவறு செய்தீர்கள் என்று கருதக்கூடாது.

மற்றொரு அம்சம் அடைப்புக்குறிகளின் விரிவாக்கத்துடன் தொடர்புடையது. தயவுசெய்து கவனிக்கவும்: அவர்களுக்கு முன்னால் "மைனஸ்" இருந்தால், அதை அகற்றுவோம், ஆனால் அடைப்புக்குறிக்குள் அடையாளங்களை மாற்றுகிறோம் எதிர். பின்னர் அதை நிலையான வழிமுறைகளின்படி திறக்கலாம்: மேலே உள்ள கணக்கீடுகளில் நாம் பார்த்ததைப் பெறுவோம்.

இந்த எளிய உண்மையைப் புரிந்துகொள்வது, உயர்நிலைப் பள்ளியில் முட்டாள்தனமான மற்றும் புண்படுத்தும் தவறுகளைத் தவிர்க்க உதவும்.

சிக்கலான நேரியல் சமன்பாடுகளைத் தீர்ப்பது

இன்னும் சிக்கலான சமன்பாடுகளுக்கு செல்லலாம். இப்போது கட்டுமானங்கள் மிகவும் சிக்கலானதாக மாறும் மற்றும் பல்வேறு மாற்றங்களைச் செய்யும்போது ஒரு இருபடி செயல்பாடு தோன்றும். இருப்பினும், நீங்கள் இதைப் பற்றி பயப்படக்கூடாது, ஏனென்றால் ஆசிரியரின் நோக்கத்தின்படி, நாம் ஒரு நேரியல் சமன்பாட்டைத் தீர்த்தால், மாற்றத்தின் செயல்பாட்டில் ஒரு இருபடி செயல்பாட்டைக் கொண்ட அனைத்து மோனோமியல்களும் அவசியம் குறைக்கப்படும்.

எடுத்துக்காட்டு #1

வெளிப்படையாக, முதல் படி அடைப்புக்குறிகளைத் திறக்க வேண்டும். இதை மிகவும் கவனமாக செய்வோம்:

இப்போது தனியுரிமையை எடுத்துக் கொள்வோம்:

\[-x+6((x)^(2))-6((x)^(2))+x=-12\]

இது போன்ற சில இங்கே:

வெளிப்படையாக, இந்த சமன்பாட்டிற்கு தீர்வுகள் இல்லை, எனவே பதிலில் பின்வருமாறு எழுதுகிறோம்:

\[\வகை \]

அல்லது வேர்கள் இல்லை.

எடுத்துக்காட்டு #2

நாங்கள் அதே படிகளைச் செய்கிறோம். முதல் படி:

எல்லாவற்றையும் ஒரு மாறியுடன் இடதுபுறமாக நகர்த்துவோம், அது இல்லாமல் - வலதுபுறம்:

இது போன்ற சில இங்கே:

வெளிப்படையாக, இந்த நேரியல் சமன்பாட்டிற்கு தீர்வு இல்லை, எனவே இதை இப்படி எழுதுகிறோம்:

\[\varnothing\],

அல்லது வேர்கள் இல்லை.

தீர்வின் நுணுக்கங்கள்

இரண்டு சமன்பாடுகளும் முழுமையாக தீர்க்கப்படுகின்றன. இந்த இரண்டு வெளிப்பாடுகளின் எடுத்துக்காட்டில், எளிமையான நேரியல் சமன்பாடுகளில் கூட, எல்லாம் அவ்வளவு எளிதல்ல என்பதை நாங்கள் மீண்டும் உறுதிசெய்தோம்: ஒன்று, அல்லது எதுவுமில்லை, அல்லது எண்ணற்ற பல இருக்கலாம். எங்கள் விஷயத்தில், இரண்டு சமன்பாடுகளைக் கருத்தில் கொண்டோம், இரண்டிலும் வெறுமனே வேர்கள் இல்லை.

ஆனால் நான் மற்றொரு உண்மைக்கு உங்கள் கவனத்தை ஈர்க்க விரும்புகிறேன்: அடைப்புக்குறிகளுடன் எவ்வாறு வேலை செய்வது மற்றும் அவர்களுக்கு முன்னால் ஒரு கழித்தல் அடையாளம் இருந்தால் அவற்றை எவ்வாறு விரிவாக்குவது. இந்த வெளிப்பாட்டைக் கவனியுங்கள்:

திறப்பதற்கு முன், நீங்கள் எல்லாவற்றையும் "x" ஆல் பெருக்க வேண்டும். தயவுசெய்து கவனிக்கவும்: பெருக்கவும் ஒவ்வொரு தனிப்பட்ட கால. உள்ளே இரண்டு சொற்கள் உள்ளன - முறையே, இரண்டு சொற்கள் மற்றும் பெருக்கப்படுகிறது.

இந்த வெளித்தோற்றத்தில் அடிப்படை, ஆனால் மிக முக்கியமான மற்றும் ஆபத்தான மாற்றங்கள் முடிந்த பின்னரே, அதற்குப் பிறகு ஒரு கழித்தல் அடையாளம் உள்ளது என்ற பார்வையில் அடைப்புக்குறியைத் திறக்க முடியும். ஆம், ஆம்: இப்போதுதான், மாற்றங்கள் செய்யப்படும்போது, ​​அடைப்புக்குறிகளுக்கு முன்னால் ஒரு கழித்தல் அடையாளம் இருப்பதை நினைவில் கொள்கிறோம், அதாவது கீழே உள்ள அனைத்தும் அறிகுறிகளை மாற்றுகிறது. அதே நேரத்தில், அடைப்புக்குறிகள் மறைந்துவிடும், மிக முக்கியமாக, முன் "கழித்தல்" கூட மறைந்துவிடும்.

இரண்டாவது சமன்பாட்டிலும் இதைச் செய்கிறோம்:

இந்த சிறிய, முக்கியமற்ற உண்மைகளுக்கு நான் கவனம் செலுத்துவது தற்செயல் நிகழ்வு அல்ல. சமன்பாடுகளைத் தீர்ப்பது எப்போதுமே அடிப்படை மாற்றங்களின் வரிசையாக இருப்பதால், எளிய செயல்களை தெளிவாகவும் திறமையாகவும் செய்ய இயலாமை உயர்நிலைப் பள்ளி மாணவர்கள் என்னிடம் வந்து மீண்டும் அத்தகைய எளிய சமன்பாடுகளைத் தீர்க்க கற்றுக்கொள்கிறார்கள்.

நிச்சயமாக, நீங்கள் இந்த திறன்களை தன்னியக்கத்திற்கு மேம்படுத்தும் நாள் வரும். நீங்கள் இனி ஒவ்வொரு முறையும் பல மாற்றங்களைச் செய்ய வேண்டியதில்லை, எல்லாவற்றையும் ஒரே வரியில் எழுதுவீர்கள். ஆனால் நீங்கள் கற்றுக் கொண்டிருக்கும் போது, ​​ஒவ்வொரு செயலையும் தனித்தனியாக எழுத வேண்டும்.

இன்னும் சிக்கலான நேரியல் சமன்பாடுகளைத் தீர்ப்பது

நாம் இப்போது தீர்க்கப் போவதை எளிமையான பணி என்று அழைக்க முடியாது, ஆனால் பொருள் அப்படியே உள்ளது.

பணி எண் 1

\[\இடது(7x+1 \வலது)\இடது(3x-1 \வலது)-21((x)^(2))=3\]

முதல் பகுதியில் உள்ள அனைத்து கூறுகளையும் பெருக்குவோம்:

பின்வாங்குவோம்:

இது போன்ற சில இங்கே:

கடைசி படி செய்வோம்:

\[\frac(-4x)(4)=\frac(4)(-4)\]

இங்கே எங்கள் இறுதி பதில். மேலும், தீர்க்கும் செயல்பாட்டில் இருபடி சார்புடன் கூடிய குணகங்கள் இருந்தபோதிலும், அவை பரஸ்பரம் ரத்து செய்யப்பட்டன, இது சமன்பாட்டை சரியாக நேரியல் அல்ல, சதுரமாக மாற்றுகிறது.

பணி #2

\[\இடது(1-4x \வலது)\இடது(1-3x \வலது)=6x\இடது(2x-1 \வலது)\]

முதல் படியை கவனமாகச் செய்வோம்: முதல் அடைப்புக்குறியில் உள்ள ஒவ்வொரு உறுப்பையும் இரண்டாவதாக உள்ள ஒவ்வொரு தனிமத்தால் பெருக்கவும். மொத்தத்தில், மாற்றங்களுக்குப் பிறகு நான்கு புதிய சொற்கள் பெறப்பட வேண்டும்:

இப்போது ஒவ்வொரு காலத்திலும் பெருக்கத்தை கவனமாக செய்யுங்கள்:

"x" உடன் உள்ள விதிமுறைகளை இடதுபுறமாகவும், இல்லாமல் - வலதுபுறமாகவும் நகர்த்துவோம்:

\[-3x-4x+12((x)^(2))-12((x)^(2))+6x=-1\]

இதே போன்ற சொற்கள் இங்கே:

எங்களுக்கு உறுதியான பதில் கிடைத்துள்ளது.

தீர்வின் நுணுக்கங்கள்

இந்த இரண்டு சமன்பாடுகளைப் பற்றிய மிக முக்கியமான கருத்து இதுதான்: ஒரு சொல்லுக்கு மேல் உள்ள அடைப்புக்குறிகளைப் பெருக்கத் தொடங்கியவுடன், இது பின்வரும் விதியின்படி செய்யப்படுகிறது: முதல் சொல்லிலிருந்து முதல் வார்த்தையை எடுத்து ஒவ்வொரு உறுப்புடன் பெருக்குகிறோம். இரண்டாவது இருந்து; பின்னர் நாம் முதல் உறுப்பிலிருந்து இரண்டாவது உறுப்பை எடுத்து, அதே போல் இரண்டாவதிலிருந்து ஒவ்வொரு உறுப்புடன் பெருக்குகிறோம். இதன் விளைவாக, நாங்கள் நான்கு சொற்களைப் பெறுகிறோம்.

இயற்கணிதத் தொகையில்

கடைசி உதாரணத்துடன், இயற்கணிதத் தொகை என்றால் என்ன என்பதை மாணவர்களுக்கு நினைவூட்ட விரும்புகிறேன். கிளாசிக்கல் கணிதத்தில், $1-7$ என்பது எளிமையான கட்டுமானத்தைக் குறிக்கும்: ஒன்றிலிருந்து ஏழரைக் கழிக்கிறோம். இயற்கணிதத்தில், நாம் இதன் மூலம் பின்வருவனவற்றைக் குறிக்கிறோம்: "ஒன்று" என்ற எண்ணுடன் மற்றொரு எண்ணைச் சேர்க்கிறோம், அதாவது "மைனஸ் ஏழு." இந்த இயற்கணிதத் தொகை வழக்கமான எண்கணிதத் தொகையிலிருந்து வேறுபடுகிறது.

அனைத்து மாற்றங்களையும், ஒவ்வொரு கூட்டல் மற்றும் பெருக்கத்தையும் செய்யும்போது, ​​​​மேலே விவரிக்கப்பட்டதைப் போன்ற கட்டுமானங்களைப் பார்க்கத் தொடங்கினால், பல்லுறுப்புக்கோவைகள் மற்றும் சமன்பாடுகளுடன் பணிபுரியும் போது இயற்கணிதத்தில் உங்களுக்கு எந்த பிரச்சனையும் இருக்காது.

முடிவில், நாம் பார்த்ததை விட இன்னும் சிக்கலான இரண்டு எடுத்துக்காட்டுகளைப் பார்ப்போம், அவற்றைத் தீர்க்க, எங்கள் நிலையான வழிமுறையை சற்று விரிவுபடுத்த வேண்டும்.

ஒரு பின்னத்துடன் சமன்பாடுகளைத் தீர்ப்பது

அத்தகைய பணிகளைத் தீர்க்க, எங்கள் வழிமுறையில் மேலும் ஒரு படி சேர்க்கப்பட வேண்டும். ஆனால் முதலில், நான் எங்கள் வழிமுறையை நினைவூட்டுகிறேன்:

1. அடைப்புக்குறிகளைத் திறக்கவும்.
2. தனி மாறிகள்.
3. இதேபோல் கொண்டு வாருங்கள்.
4. ஒரு காரணி மூலம் வகுக்கவும்.

ஐயோ, இந்த அற்புதமான அல்காரிதம், அதன் அனைத்து செயல்திறனுக்காகவும், நமக்கு முன்னால் பின்னங்கள் இருக்கும்போது முற்றிலும் பொருத்தமானது அல்ல. நாம் கீழே காண்பதில், இரண்டு சமன்பாடுகளிலும் இடது மற்றும் வலதுபுறத்தில் ஒரு பின்னம் உள்ளது.

இந்த வழக்கில் எப்படி வேலை செய்வது? ஆம், இது மிகவும் எளிமையானது! இதைச் செய்ய, நீங்கள் அல்காரிதத்தில் இன்னும் ஒரு படியைச் சேர்க்க வேண்டும், இது முதல் செயலுக்கு முன்னும் பின்னும் செய்யப்படலாம், அதாவது பின்னங்களிலிருந்து விடுபட. எனவே, அல்காரிதம் பின்வருமாறு இருக்கும்:

1. பின்னங்களை அகற்றவும்.
2. அடைப்புக்குறிகளைத் திறக்கவும்.
3. தனி மாறிகள்.
4. இதேபோல் கொண்டு வாருங்கள்.
5. ஒரு காரணி மூலம் வகுக்கவும்.

"பிரிவுகளை அகற்றுவது" என்றால் என்ன? முதல் நிலையான படிக்குப் பிறகும் அதற்கு முன்பும் இதை ஏன் செய்ய முடியும்? உண்மையில், எங்கள் விஷயத்தில், அனைத்து பின்னங்களும் வகுப்பின் அடிப்படையில் எண்களாகும், அதாவது. எல்லா இடங்களிலும் வகுத்தல் என்பது ஒரு எண் மட்டுமே. எனவே, சமன்பாட்டின் இரு பகுதிகளையும் இந்த எண்ணால் பெருக்கினால், பின்னங்களை அகற்றுவோம்.

எடுத்துக்காட்டு #1

\[\frac(\left(2x+1 \right)\left(2x-3 \right))(4)=((x)^(2))-1\]

இந்த சமன்பாட்டில் உள்ள பின்னங்களை அகற்றுவோம்:

\[\frac(\left(2x+1 \right)\left(2x-3 \right)\cdot 4)(4)=\left(((x)^(2))-1 \right)\cdot நான்கு\]

தயவுசெய்து கவனிக்கவும்: எல்லாம் ஒரு முறை "நான்கு" ஆல் பெருக்கப்படுகிறது, அதாவது. உங்களிடம் இரண்டு அடைப்புக்குறிகள் இருப்பதால் அவை ஒவ்வொன்றையும் "நான்கால்" பெருக்க வேண்டும் என்று அர்த்தமல்ல. எழுதுவோம்:

\[\left(2x+1 \right)\left(2x-3 \right)=\left(((x)^(2))-1 \right)\cdot 4\]

இப்போது அதை திறப்போம்:

ஒரு மாறியின் தனிமையை நாங்கள் செய்கிறோம்:

இதே போன்ற சொற்களின் குறைப்பை நாங்கள் மேற்கொள்கிறோம்:

\[-4x=-1\இடது| :\இடது(-4 \வலது) \வலது.\]

\[\frac(-4x)(-4)=\frac(-1)(-4)\]

நாங்கள் இறுதி தீர்வைப் பெற்றுள்ளோம், இரண்டாவது சமன்பாட்டிற்கு செல்கிறோம்.

எடுத்துக்காட்டு #2

\[\frac(\left(1-x \right)\left(1+5x \right))(5)+((x)^(2))=1\]

இங்கே நாம் ஒரே மாதிரியான செயல்களைச் செய்கிறோம்:

\[\frac(\left(1-x \right)\left(1+5x \right)\cdot 5)(5)+((x)^(2))\cdot 5=5\]

\[\frac(4x)(4)=\frac(4)(4)\]

பிரச்சினை தீர்ந்துவிட்டது.

உண்மையில், இன்று நான் சொல்ல விரும்பியதெல்லாம் இதுதான்.

முக்கிய புள்ளிகள்

முக்கிய கண்டுபிடிப்புகள் பின்வருமாறு:

• நேரியல் சமன்பாடுகளைத் தீர்ப்பதற்கான அல்காரிதத்தை அறிந்து கொள்ளுங்கள்.
• அடைப்புக்குறிகளைத் திறக்கும் திறன்.
• உங்களிடம் எங்காவது இருபடி செயல்பாடுகள் இருந்தால் கவலைப்பட வேண்டாம், பெரும்பாலும், மேலும் மாற்றங்களின் செயல்பாட்டில், அவை குறைக்கப்படும்.
• நேரியல் சமன்பாடுகளில் உள்ள வேர்கள், எளிமையானவை கூட, மூன்று வகைகளாகும்: ஒரு ஒற்றை ரூட், முழு எண் கோடு ஒரு ரூட், வேர்கள் எதுவும் இல்லை.

இந்த பாடம் அனைத்து கணிதத்தையும் மேலும் புரிந்துகொள்ள எளிய, ஆனால் மிக முக்கியமான தலைப்பில் தேர்ச்சி பெற உதவும் என்று நம்புகிறேன். ஏதாவது தெளிவாக தெரியவில்லை என்றால், தளத்திற்குச் சென்று, அங்கு வழங்கப்பட்ட எடுத்துக்காட்டுகளைத் தீர்க்கவும். காத்திருங்கள், இன்னும் பல சுவாரஸ்யமான விஷயங்கள் உங்களுக்காகக் காத்திருக்கின்றன!

ஆன்லைன் பின்னம் கால்குலேட்டர் பின்னங்களுடன் எளிய எண்கணித செயல்பாடுகளைச் செய்ய உங்களை அனுமதிக்கிறது: பின்னங்களின் கூட்டல், பின்னங்களின் கழித்தல், பின்னங்களின் பெருக்கல், பின்னங்களின் பிரிவு. கணக்கீடுகளைச் செய்ய, இரண்டு பின்னங்களின் எண்கள் மற்றும் வகுப்பிகளுடன் தொடர்புடைய புலங்களை நிரப்பவும்.

கணிதத்தில் பின்னம்ஒரு அலகு அல்லது அதன் பல பகுதிகளைக் குறிக்கும் எண் அழைக்கப்படுகிறது.

ஒரு பொதுவான பின்னம் இரண்டு எண்களாக எழுதப்படுகிறது, பொதுவாக ஒரு கிடைமட்ட கோட்டால் பிரிக்கப்படுகிறது, இது பிரிவு அடையாளத்தைக் குறிக்கிறது. பட்டைக்கு மேலே உள்ள எண்ணை எண் என்று அழைக்கப்படுகிறது. பட்டைக்கு கீழே உள்ள எண் வகுத்தல் எனப்படும். ஒரு பகுதியின் வகுத்தல், முழுமையும் பிரிக்கப்பட்டுள்ள சம பாகங்களின் எண்ணிக்கையைக் காட்டுகிறது, மேலும் பின்னத்தின் எண்ணிக்கையானது எடுக்கப்பட்ட முழுப் பகுதிகளின் எண்ணிக்கையையும் காட்டுகிறது.

பின்னங்கள் சரி மற்றும் தவறு.

• ஒரு சரியான பின்னம், அதன் எண் வகுப்பை விட குறைவாக உள்ளது.
• ஒரு முறையற்ற பின்னம் என்பது வகுப்பை விட எண் அதிகமாக இருக்கும் போது.

ஒரு கலப்பு பின்னம் என்பது முழு எண்ணாகவும் சரியான பின்னமாகவும் எழுதப்பட்ட பின்னமாகும், மேலும் இந்த எண் மற்றும் பின்னம் பகுதியின் கூட்டுத்தொகையாக புரிந்து கொள்ளப்படுகிறது. அதன்படி, முழு எண் பகுதி இல்லாத பின்னம் ஒரு எளிய பின்னம் என்று அழைக்கப்படுகிறது. எந்த கலப்பு பின்னமும் முறையற்ற எளிய பின்னமாக மாற்றப்படும்.

ஒரு கலப்பு பின்னத்தை சாதாரணமாக மாற்ற, முழு எண் பகுதியின் பெருக்கத்தையும் பிரிவின் எண்ணையும் சேர்க்க வேண்டியது அவசியம்:

ஒரு சாதாரண பின்னத்தை ஒரு கலவையாக மாற்றுவது எப்படி

ஒரு சாதாரண பின்னத்தை கலவையாக மாற்ற, நீங்கள் கண்டிப்பாக:

1. ஒரு பகுதியின் எண்ணை அதன் வகுப்பால் வகுக்கவும்
2. பிரிவின் முடிவு முழு எண் பகுதியாக இருக்கும்
3. கிளையின் எஞ்சிய பகுதி எண்களாக இருக்கும்

ஒரு பொதுவான பகுதியை தசமமாக மாற்றுவது எப்படி

ஒரு பகுதியை தசமமாக மாற்ற, அதன் எண்ணை வகுப்பால் வகுக்க வேண்டும்.

ஒரு தசமத்தை பொதுவான பின்னமாக மாற்ற, நீங்கள் கண்டிப்பாக:

ஒரு பகுதியை ஒரு சதவீதமாக மாற்றுவது எப்படி

ஒரு சாதாரண அல்லது கலப்பு பகுதியை ஒரு சதவீதமாக மாற்ற, நீங்கள் அதை தசம பின்னமாக மாற்றி 100 ஆல் பெருக்க வேண்டும்.

சதவீதங்களை பின்னங்களாக மாற்றுவது எப்படி

சதவீதங்களை பின்னங்களாக மாற்ற, சதவீதங்களிலிருந்து தசமப் பகுதியைப் பெறுவது அவசியம் (100 ஆல் வகுத்தல்), அதன் விளைவாக வரும் தசமப் பகுதியை சாதாரணமாக மாற்றவும்.

பின்னங்கள் சேர்த்தல்

இரண்டு பின்னங்களைச் சேர்ப்பதற்கான வழிமுறை பின்வருமாறு:

1. பின்னங்களை அவற்றின் எண்களைச் சேர்ப்பதன் மூலம் சேர்க்கவும்.

பின்னங்களின் கழித்தல்

இரண்டு பின்னங்களைக் கழிக்கும்போது செயல்களின் அல்காரிதம்:

1. கலப்பு பின்னங்களை பொதுவான பின்னங்களாக மாற்றவும் (முழுப் பகுதியை அகற்றவும்).
2. பின்னங்களை ஒரு பொதுவான வகுப்பிற்கு கொண்டு வாருங்கள். இதைச் செய்ய, நீங்கள் முதல் பகுதியின் எண் மற்றும் வகுப்பை இரண்டாவது பின்னத்தின் வகுப்பால் பெருக்க வேண்டும், மேலும் இரண்டாவது பகுதியின் எண் மற்றும் வகுப்பை முதல் பின்னத்தின் வகுப்பால் பெருக்க வேண்டும்.
3. முதல் பகுதியின் எண்ணிலிருந்து இரண்டாவது பின்னத்தின் எண்ணைக் கழிப்பதன் மூலம் ஒரு பகுதியை மற்றொன்றிலிருந்து கழிக்கவும்.
4. எண் மற்றும் வகுப்பின் மிகப் பெரிய பொது வகுப்பினை (GCD) கண்டறிந்து, எண் மற்றும் வகுப்பினை GCD ஆல் வகுப்பதன் மூலம் பின்னத்தைக் குறைக்கவும்.
5. இறுதிப் பகுதியின் எண் வகுப்பினை விட அதிகமாக இருந்தால், முழுப் பகுதியையும் தேர்ந்தெடுக்கவும்.

பின்னங்களின் பெருக்கல்

இரண்டு பின்னங்களை பெருக்கும் போது செயல்களின் அல்காரிதம்:

1. கலப்பு பின்னங்களை பொதுவான பின்னங்களாக மாற்றவும் (முழுப் பகுதியை அகற்றவும்).
2. எண் மற்றும் வகுப்பின் மிகப் பெரிய பொது வகுப்பினை (GCD) கண்டறிந்து, எண் மற்றும் வகுப்பினை GCD ஆல் வகுப்பதன் மூலம் பின்னத்தைக் குறைக்கவும்.
3. இறுதிப் பகுதியின் எண் வகுப்பினை விட அதிகமாக இருந்தால், முழுப் பகுதியையும் தேர்ந்தெடுக்கவும்.

பின்னங்களின் பிரிவு

இரண்டு பின்னங்களை பிரிக்கும்போது செயல்களின் வழிமுறை:

1. கலப்பு பின்னங்களை பொதுவான பின்னங்களாக மாற்றவும் (முழுப் பகுதியை அகற்றவும்).
2. பின்னங்களைப் பிரிக்க, நீங்கள் அதன் எண் மற்றும் வகுப்பினை மாற்றுவதன் மூலம் இரண்டாவது பகுதியை மாற்ற வேண்டும், பின்னர் பின்னங்களைப் பெருக்க வேண்டும்.
3. முதல் பின்னத்தின் எண்ணிக்கையை இரண்டாவது பின்னத்தின் எண் மற்றும் முதல் பின்னத்தின் வகுப்பை இரண்டாவது வகுப்பால் பெருக்கவும்.
4. எண் மற்றும் வகுப்பின் மிகப் பெரிய பொது வகுப்பினை (GCD) கண்டறிந்து, எண் மற்றும் வகுப்பினை GCD ஆல் வகுப்பதன் மூலம் பின்னத்தைக் குறைக்கவும்.
5. இறுதிப் பகுதியின் எண் வகுப்பினை விட அதிகமாக இருந்தால், முழுப் பகுதியையும் தேர்ந்தெடுக்கவும்.

ஆன்லைன் கால்குலேட்டர்கள் மற்றும் மாற்றிகள்:

தெரியாத ஒரு சமன்பாடு, அடைப்புக்குறிகளைத் திறந்து, போன்ற சொற்களைக் குறைத்த பிறகு, வடிவம் பெறுகிறது

கோடாரி + பி = 0, a மற்றும் b ஆகியவை தன்னிச்சையான எண்கள் எனப்படும் நேரியல் சமன்பாடு தெரியாத ஒருவருடன். இந்த நேரியல் சமன்பாடுகளை எவ்வாறு தீர்ப்பது என்பதை இன்று கண்டுபிடிப்போம்.

எடுத்துக்காட்டாக, அனைத்து சமன்பாடுகளும்:

2x + 3 \u003d 7 - 0.5x; 0.3x = 0; x / 2 + 3 \u003d 1/2 (x - 2) - நேரியல்.

சமன்பாட்டை உண்மையான சமத்துவமாக மாற்றும் தெரியாதவற்றின் மதிப்பு அழைக்கப்படுகிறது முடிவு அல்லது சமன்பாட்டின் வேர் .

எடுத்துக்காட்டாக, சமன்பாடு 3x + 7 \u003d 13 இல் தெரியாத x க்கு பதிலாக எண் 2 ஐ மாற்றினால், சரியான சமத்துவம் 3 2 + 7 \u003d 13 ஐப் பெறுகிறோம். எனவே, மதிப்பு x \u003d 2 தீர்வு அல்லது சமன்பாட்டின் வேர்.

மேலும் x \u003d 3 என்பது 3x + 7 \u003d 13 என்ற சமன்பாட்டை உண்மையான சமத்துவமாக மாற்றாது, ஏனெனில் 3 2 + 7 ≠ 13. எனவே, மதிப்பு x \u003d 3 சமன்பாட்டின் ஒரு தீர்வு அல்லது ரூட் அல்ல.

எந்த நேரியல் சமன்பாடுகளின் தீர்வும் படிவத்தின் சமன்பாடுகளின் தீர்வுக்கு குறைக்கப்படுகிறது

கோடாரி + பி = 0.

சமன்பாட்டின் இடது பக்கத்திலிருந்து வலப்புறத்திற்கு இலவச காலத்தை மாற்றுகிறோம், அதே நேரத்தில் b க்கு முன்னால் உள்ள அடையாளத்தை எதிர்மாறாக மாற்றுகிறோம்.

a ≠ 0 என்றால், x = – b/a .

எடுத்துக்காட்டு 1 3x + 2 =11 சமன்பாட்டை தீர்க்கவும்.

சமன்பாட்டின் இடது பக்கத்திலிருந்து 2 ஐ வலது பக்கம் மாற்றுகிறோம், 2 க்கு முன்னால் உள்ள அடையாளத்தை எதிர்மாறாக மாற்றுகிறோம்.
3x \u003d 11 - 2.

பிறகு கழிப்போம்
3x = 9.

x ஐக் கண்டுபிடிக்க, நீங்கள் அறியப்பட்ட காரணி மூலம் தயாரிப்பைப் பிரிக்க வேண்டும், அதாவது,
x = 9:3.

எனவே x = 3 என்பது சமன்பாட்டின் தீர்வு அல்லது மூலமாகும்.

பதில்: x = 3.

a = 0 மற்றும் b = 0 எனில், பின்னர் நாம் சமன்பாடு 0x \u003d 0 ஐப் பெறுகிறோம். இந்தச் சமன்பாட்டில் எண்ணற்ற தீர்வுகள் உள்ளன, ஏனெனில் எந்த எண்ணையும் 0 ஆல் பெருக்கும்போது, ​​நமக்கு 0 கிடைக்கும், ஆனால் b என்பதும் 0. இந்தச் சமன்பாட்டின் தீர்வு எந்த எண்ணாகும்.

உதாரணம் 2சமன்பாடு 5(x - 3) + 2 = 3 (x - 4) + 2x - 1 ஐ தீர்க்கவும்.

அடைப்புக்குறிகளை விரிவாக்குவோம்:
5x - 15 + 2 \u003d 3x - 12 + 2x - 1.

5x - 3x - 2x \u003d - 12 - 1 + 15 - 2.

இங்கே ஒத்த உறுப்பினர்கள்:
0x = 0.

பதில்: x என்பது எந்த எண்.

a = 0 மற்றும் b ≠ 0 எனில், பிறகு சமன்பாடு 0x = - b கிடைக்கும். இந்த சமன்பாட்டிற்கு தீர்வுகள் இல்லை, ஏனெனில் எந்த எண்ணையும் 0 ஆல் பெருக்கும்போது, ​​நமக்கு 0 கிடைக்கும், ஆனால் b ≠ 0.

எடுத்துக்காட்டு 3 x + 8 = x + 5 சமன்பாட்டைத் தீர்க்கவும்.

இடதுபுறத்தில் தெரியாதவற்றைக் கொண்ட விதிமுறைகளையும், வலதுபுறத்தில் இலவச விதிமுறைகளையும் தொகுக்கலாம்:
x - x \u003d 5 - 8.

இங்கே ஒத்த உறுப்பினர்கள்:
0x = - 3.

பதில்: தீர்வுகள் இல்லை.

அதன் மேல் படம் 1 நேரியல் சமன்பாட்டைத் தீர்ப்பதற்கான திட்டம் காட்டப்பட்டுள்ளது

ஒரு மாறி மூலம் சமன்பாடுகளைத் தீர்ப்பதற்கான பொதுவான திட்டத்தை உருவாக்குவோம். உதாரணம் 4 இன் தீர்வைக் கவனியுங்கள்.

எடுத்துக்காட்டு 4 சமன்பாட்டைத் தீர்ப்போம்

1) சமன்பாட்டின் அனைத்து விதிமுறைகளையும் 12 க்கு சமமான வகுப்பின் குறைந்தபட்ச பொது மடங்குகளால் பெருக்கவும்.

2) குறைத்த பிறகு நாம் பெறுகிறோம்
4 (x - 4) + 3 2 (x + 1) - 12 = 6 5 (x - 3) + 24x - 2 (11x + 43)

3) தெரியாத மற்றும் இலவச உறுப்பினர்களைக் கொண்ட உறுப்பினர்களைப் பிரிக்க, அடைப்புக்குறிகளைத் திறக்கவும்:
4x - 16 + 6x + 6 - 12 \u003d 30x - 90 + 24x - 22x - 86.

4) தெரியாதவற்றைக் கொண்ட விதிமுறைகளை ஒரு பகுதியில் தொகுக்கிறோம், மற்றொன்றில் - இலவச விதிமுறைகள்:
4x + 6x - 30x - 24x + 22x \u003d - 90 - 86 + 16 - 6 + 12.

5) இதே போன்ற உறுப்பினர்கள் இங்கே உள்ளனர்:
- 22x = - 154.

6) வகுக்க - 22 , நாம் பெறுகிறோம்
x = 7.

நீங்கள் பார்க்க முடியும் என, சமன்பாட்டின் வேர் ஏழு.

பொதுவாக, அத்தகைய சமன்பாடுகளை பின்வருமாறு தீர்க்கலாம்:

a) சமன்பாட்டை முழு எண் வடிவத்திற்கு கொண்டு வரவும்;

b) திறந்த அடைப்புக்குறிகள்;

c) சமன்பாட்டின் ஒரு பகுதியில் தெரியாதவற்றைக் கொண்ட சொற்களையும், மற்றொன்றில் இலவச சொற்களையும் தொகுத்தல்;

ஈ) ஒத்த உறுப்பினர்களைக் கொண்டு வருதல்;

e) aх = b வடிவத்தின் சமன்பாட்டைத் தீர்க்கவும், இது போன்ற விதிமுறைகளைக் கொண்டு வந்த பிறகு பெறப்பட்டது.

இருப்பினும், இந்த திட்டம் ஒவ்வொரு சமன்பாட்டிற்கும் தேவையில்லை. பல எளிய சமன்பாடுகளைத் தீர்க்கும் போது, ​​முதலில் இருந்து தொடங்காமல், இரண்டாவதாக ( உதாரணமாக. 2), மூன்றாவது ( உதாரணமாக. 13) மற்றும் ஐந்தாவது கட்டத்தில் இருந்து கூட, உதாரணம் 5 இல் உள்ளது.

உதாரணம் 5சமன்பாட்டை 2x = 1/4 தீர்க்கவும்.

தெரியாத x \u003d 1/4: 2,
x = 1/8 .

முக்கிய மாநிலத் தேர்வில் எதிர்கொள்ளும் சில நேரியல் சமன்பாடுகளின் தீர்வைக் கவனியுங்கள்.

எடுத்துக்காட்டு 6சமன்பாடு 2 (x + 3) = 5 - 6x ஐ தீர்க்கவும்.

2x + 6 = 5 - 6x

2x + 6x = 5 - 6

பதில்: - 0.125

எடுத்துக்காட்டு 7சமன்பாட்டை தீர்க்கவும் - 6 (5 - 3x) \u003d 8x - 7.

– 30 + 18x = 8x – 7

18x - 8x = - 7 +30

பதில்: 2.3

எடுத்துக்காட்டு 8 சமன்பாட்டை தீர்க்கவும்

3(3x - 4) = 4 7x + 24

9x - 12 = 28x + 24

9x - 28x = 24 + 12

எடுத்துக்காட்டு 9 f (x + 2) = 3 7's என்றால் f(6) ஐக் கண்டறியவும்

தீர்வு

நாம் f(6) ஐக் கண்டுபிடிக்க வேண்டும், மேலும் f (x + 2)
பின்னர் x + 2 = 6.

நேரியல் சமன்பாட்டை x + 2 = 6 தீர்க்கிறோம்,
நாம் x \u003d 6 - 2, x \u003d 4 ஐப் பெறுகிறோம்.

x = 4 என்றால்
f(6) = 3 7-4 = 3 3 = 27

பதில்: 27.

உங்களிடம் இன்னும் கேள்விகள் இருந்தால், சமன்பாடுகளின் தீர்வை இன்னும் முழுமையாக சமாளிக்க விருப்பம் உள்ளது, அட்டவணையில் எனது பாடங்களுக்கு பதிவு செய்யவும். உங்களுக்கு உதவ நான் மகிழ்ச்சியடைவேன்!

எங்கள் ஆசிரியர் ஓல்கா அலெக்ஸாண்ட்ரோவ்னாவிடமிருந்து புதிய வீடியோ டுடோரியலைப் பார்க்கவும் TutorOnline பரிந்துரைக்கிறது, இது நேரியல் சமன்பாடுகள் மற்றும் பிற இரண்டையும் புரிந்துகொள்ள உதவும்.

தளத்தில், பொருளின் முழு அல்லது பகுதி நகலுடன், மூலத்திற்கான இணைப்பு தேவை.

பகுத்தறிவற்ற சமன்பாடுகள் என்றால் என்ன, அவற்றை எவ்வாறு தீர்ப்பது

தீவிரத்தின் அடையாளத்தின் கீழ் அல்லது ஒரு பகுதியளவு சக்திக்கு உயர்த்துவதற்கான அடையாளத்தின் கீழ் மாறி கொண்டிருக்கும் சமன்பாடுகள் என்று அழைக்கப்படுகின்றன. பகுத்தறிவற்ற. நாம் ஒரு பகுதியளவு சக்தியைக் கையாளும் போது, ​​சமன்பாட்டைத் தீர்ப்பதற்கான பல கணித செயல்பாடுகளை நாம் இழக்கிறோம், எனவே பகுத்தறிவற்ற சமன்பாடுகள் ஒரு சிறப்பு வழியில் தீர்க்கப்படுகின்றன.

பகுத்தறிவற்ற சமன்பாடுகள் பொதுவாக சமன்பாட்டின் இரு பக்கங்களையும் ஒரே சக்திக்கு உயர்த்துவதன் மூலம் தீர்க்கப்படுகின்றன. அதே நேரத்தில், சமன்பாட்டின் இரு பகுதிகளையும் ஒரே ஒற்றைப்படை சக்திக்கு உயர்த்துவது சமன்பாட்டின் சமமான மாற்றமாகும், மேலும் சமமான ஒன்றுக்கு சமமானதல்ல. ஒரு சமமான சக்திக்கு உயர்த்தப்பட்டால், எதிர்மறை மதிப்புகள் "இழந்தன" போன்ற அதிவேகத்தின் அம்சங்களால் இத்தகைய வேறுபாடு பெறப்படுகிறது.

ஒரு பகுத்தறிவற்ற சமன்பாட்டின் இரு பக்கங்களையும் ஒரு சக்தியாக உயர்த்துவதன் புள்ளி "பகுத்தறிவின்மை" யிலிருந்து விடுபடுவதாகும். எனவே, பகுத்தறிவற்ற சமன்பாட்டின் இரு பகுதிகளையும் நாம் உயர்த்த வேண்டும், சமன்பாட்டின் இரு பகுதிகளின் அனைத்து பகுதியளவு சக்திகளும் முழு எண்களாக மாறும். அதன் பிறகு, இந்த சமன்பாட்டிற்கான தீர்வை நீங்கள் தேடலாம், இது பகுத்தறிவற்ற சமன்பாட்டின் தீர்வுகளுடன் ஒத்துப்போகும், சம சக்திக்கு உயர்த்தும் விஷயத்தில், அடையாளம் இழக்கப்படும் மற்றும் இறுதி தீர்வுகளுக்கு சரிபார்ப்பு தேவைப்படும் மற்றும் அனைத்தும் வேலை செய்யாது.

எனவே, சமன்பாட்டின் இரு பகுதிகளையும் ஒரே சமமான சக்திக்கு உயர்த்துவதில் முக்கிய சிரமம் தொடர்புடையது - மாற்றத்தின் சமத்துவமின்மை காரணமாக, வெளிப்புற வேர்கள் தோன்றக்கூடும். எனவே, கண்டுபிடிக்கப்பட்ட அனைத்து வேர்களையும் சரிபார்க்க வேண்டியது அவசியம். கண்டுபிடிக்கப்பட்ட வேர்களைச் சரிபார்ப்பது பகுத்தறிவற்ற சமன்பாட்டைத் தீர்ப்பவர்களால் பெரும்பாலும் மறந்துவிடப்படுகிறது. பகுத்தறிவின்மையிலிருந்து விடுபடுவதற்கும் அதைத் தீர்ப்பதற்கும் ஒரு பகுத்தறிவற்ற சமன்பாட்டை உயர்த்துவது எந்த அளவிற்கு அவசியம் என்பதும் எப்போதும் தெளிவாகத் தெரியவில்லை. எங்களின் ஸ்மார்ட் கால்குலேட்டர் ஒரு பகுத்தறிவற்ற சமன்பாட்டைத் தீர்க்க வடிவமைக்கப்பட்டுள்ளது மற்றும் அனைத்து வேர்களையும் தானாகவே சரிபார்க்கிறது, இது மறதியை நீக்கும்.

பகுத்தறிவற்ற சமன்பாடுகளின் இலவச ஆன்லைன் கால்குலேட்டர்

எங்களின் இலவச தீர்வியானது, இணையத்தில் எந்த ஒரு சிக்கலான சமன்பாட்டையும் சில நொடிகளில் தீர்க்க உங்களை அனுமதிக்கும். நீங்கள் செய்ய வேண்டியது உங்கள் தரவை கால்குலேட்டரில் உள்ளிடுவது மட்டுமே. எங்கள் இணையதளத்தில் சமன்பாட்டை எவ்வாறு தீர்ப்பது என்பதையும் நீங்கள் அறிந்து கொள்ளலாம். உங்களிடம் ஏதேனும் கேள்விகள் இருந்தால், அவற்றை எங்கள் VKontakte குழுவில் கேட்கலாம்.

சேவை ஒதுக்கீடு. மேட்ரிக்ஸ் கால்குலேட்டர் ஒரு மேட்ரிக்ஸ் வழியில் நேரியல் சமன்பாடுகளின் அமைப்புகளை தீர்க்க வடிவமைக்கப்பட்டுள்ளது (அதே போன்ற சிக்கல்களைத் தீர்ப்பதற்கான உதாரணத்தைப் பார்க்கவும்).

அறிவுறுத்தல். ஆன்லைன் தீர்வுக்கு, நீங்கள் சமன்பாட்டின் வகையைத் தேர்ந்தெடுத்து அதனுடன் தொடர்புடைய மெட்ரிக்குகளின் பரிமாணத்தை அமைக்க வேண்டும். A, B, C க்கு மெட்ரிக்ஸ் கொடுக்கப்பட்டால், X என்பது விரும்பிய அணி. படிவத்தின் (1), (2) மற்றும் (3) மேட்ரிக்ஸ் சமன்பாடுகள் தலைகீழ் அணி A -1 மூலம் தீர்க்கப்படுகின்றன. A X - B = C என்ற வெளிப்பாடு கொடுக்கப்பட்டால், முதலில் C + B என்ற மெட்ரிக்ஸைச் சேர்த்து, A X = D , D = C + B என்ற வெளிப்பாடுக்கான தீர்வைக் கண்டறிய வேண்டும். A*X = B 2 என்ற வெளிப்பாடு கொடுக்கப்பட்டால், அணி B முதலில் ஸ்கொயர் செய்யப்பட வேண்டும்.

மெட்ரிக்குகளின் அடிப்படை செயல்பாடுகளை நீங்கள் அறிந்துகொள்ளவும் பரிந்துரைக்கப்படுகிறது.

எடுத்துக்காட்டு #1. உடற்பயிற்சி. மேட்ரிக்ஸ் சமன்பாட்டிற்கு ஒரு தீர்வைக் கண்டறியவும்
தீர்வு. குறி:
பின்னர் அணி சமன்பாடு படிவத்தில் எழுதப்படும்: A·X·B = C.
அணி A இன் நிர்ணயம் detA=-1 ஆகும்
A ஒரு தனிமையற்ற அணி என்பதால், தலைகீழ் அணி A -1 உள்ளது. இடதுபுறத்தில் உள்ள சமன்பாட்டின் இரு பக்கங்களையும் A -1 ஆல் பெருக்கவும்: இந்த சமன்பாட்டின் இரு பக்கங்களையும் இடதுபுறத்தில் A -1 ஆல் மற்றும் வலதுபுறத்தில் B -1 ஆல் பெருக்கவும்: A -1 A X B B -1 = A -1 C B -1 . A A -1 = B B -1 = E மற்றும் E X = X E = X என்பதால், X = A -1 C B -1

தலைகீழ் அணி A -1:
தலைகீழ் அணி B -1 ஐக் கண்டறியவும்.
இடமாற்ற அணி B T:
தலைகீழ் அணி B -1:
X = A -1 C B -1 என்ற சூத்திரத்தின் மூலம் அணி X ஐத் தேடுகிறோம்

பதில்:

எடுத்துக்காட்டு #2. உடற்பயிற்சி.மேட்ரிக்ஸ் சமன்பாட்டை தீர்க்கவும்
தீர்வு. குறி:
பின்னர் அணி சமன்பாடு படிவத்தில் எழுதப்படும்: A X = B.
அணி A இன் நிர்ணயம் detA=0 ஆகும்
A ஒரு சிதைந்த அணி என்பதால் (தீர்மானி 0), எனவே, சமன்பாட்டிற்கு தீர்வு இல்லை.

எடுத்துக்காட்டு #3. உடற்பயிற்சி. மேட்ரிக்ஸ் சமன்பாட்டிற்கு ஒரு தீர்வைக் கண்டறியவும்
தீர்வு. குறி:
பின்னர் அணி சமன்பாடு வடிவத்தில் எழுதப்படும்: X·A = B.
அணி A இன் நிர்ணயம் detA=-60 ஆகும்
A ஒரு தனிமையற்ற அணி என்பதால், தலைகீழ் அணி A -1 உள்ளது. சமன்பாட்டின் வலது இருபுறமும் A -1 ஆல் பெருக்கவும்: X A A -1 = B A -1 , இதிலிருந்து X = B A -1 என்பதைக் காணலாம்.
தலைகீழ் அணி A -1 ஐக் கண்டறியவும்.
இடமாற்ற அணி A T: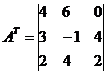
தலைகீழ் அணி A -1:
X = B A -1 என்ற சூத்திரத்தின் மூலம் அணி X ஐத் தேடுகிறோம்


பதில்: >