क्रियाओं का उपयोग करके समीकरण को हल करें। भिन्न वाले समीकरणों को ऑनलाइन हल करें। सरल रैखिक समीकरणों के वास्तविक उदाहरणों को हल करना

इस वीडियो में हम पूरे सेट का विश्लेषण करेंगे रेखीय समीकरण, जिन्हें समान एल्गोरिदम का उपयोग करके हल किया जाता है - इसीलिए उन्हें सबसे सरल कहा जाता है।

सबसे पहले, आइए परिभाषित करें: एक रैखिक समीकरण क्या है और किसे सबसे सरल कहा जाता है?

एक रैखिक समीकरण वह होता है जिसमें केवल एक चर होता है, और केवल पहली डिग्री तक।

सबसे सरल समीकरण का अर्थ है निर्माण:

एल्गोरिथम का उपयोग करके अन्य सभी रैखिक समीकरणों को सरलतम बना दिया गया है:

1. कोष्ठक, यदि कोई हो, विस्तृत करें;
2. एक चर वाले पदों को समान चिह्न के एक ओर ले जाएँ, और बिना चर वाले पदों को दूसरी ओर ले जाएँ;
3. समान चिह्न के बाएँ और दाएँ के लिए समान पद दीजिए;
4. परिणामी समीकरण को चर $x$ के गुणांक से विभाजित करें।

बेशक, यह एल्गोरिथम हमेशा मदद नहीं करता है। तथ्य यह है कि कभी-कभी इन सभी साजिशों के बाद चर $x$ का गुणांक प्राप्त होता है शून्य के बराबर. इस मामले में, दो विकल्प संभव हैं:

1. समीकरण का कोई समाधान नहीं है। उदाहरण के लिए, जब $0\cdot x=8$ जैसा कुछ निकलता है, यानी। बाईं ओर शून्य है, और दाईं ओर शून्य के अलावा कोई अन्य संख्या है। नीचे दिए गए वीडियो में हम कई कारणों पर गौर करेंगे कि यह स्थिति क्यों संभव है।
2. समाधान सभी संख्याएँ हैं। यह एकमात्र मामला है जब यह संभव है जब समीकरण को $0\cdot x=0$ की संरचना में घटा दिया गया हो। यह काफी तर्कसंगत है कि चाहे हम $x$ को किसी भी स्थान पर रखें, फिर भी यह "शून्य, शून्य के बराबर है" ही निकलेगा, यानी। सही संख्यात्मक समानता.

अब आइए देखें कि वास्तविक जीवन के उदाहरणों का उपयोग करके यह सब कैसे काम करता है।

समीकरणों को हल करने के उदाहरण

आज हम रैखिक समीकरणों और केवल सबसे सरल समीकरणों से निपट रहे हैं। सामान्य तौर पर, एक रैखिक समीकरण का मतलब किसी भी समानता से होता है जिसमें बिल्कुल एक चर होता है, और यह केवल पहली डिग्री तक जाता है।

ऐसे निर्माण लगभग उसी तरह हल किए जाते हैं:

1. सबसे पहले, आपको कोष्ठक का विस्तार करना होगा, यदि कोई हो (जैसा कि हमारे पिछले उदाहरण में है);
2. फिर समान मिला लें
3. अंत में, वेरिएबल को अलग करें, यानी वेरिएबल से जुड़ी हर चीज को - जिन शर्तों में यह निहित है - एक तरफ ले जाएं, और जो कुछ भी इसके बिना रहता है उसे दूसरी तरफ ले जाएं।

फिर, एक नियम के रूप में, आपको परिणामी समानता के प्रत्येक पक्ष पर समान देने की आवश्यकता है, और उसके बाद जो कुछ बचा है उसे "x" के गुणांक से विभाजित करना है, और हमें अंतिम उत्तर मिलेगा।

सिद्धांत रूप में, यह अच्छा और सरल दिखता है, लेकिन व्यवहार में, अनुभवी हाई स्कूल के छात्र भी काफी सरल रैखिक समीकरणों में आक्रामक गलतियाँ कर सकते हैं। आमतौर पर, त्रुटियाँ या तो कोष्ठक खोलते समय या "प्लस" और "माइनस" की गणना करते समय की जाती हैं।

इसके अलावा, ऐसा होता है कि एक रैखिक समीकरण का कोई समाधान नहीं होता है, या समाधान पूरी संख्या रेखा होती है, यानी। कोई संख्या। आज के पाठ में हम इन सूक्ष्मताओं पर गौर करेंगे। लेकिन हम शुरुआत करेंगे, जैसा कि आप पहले ही समझ चुके हैं, उसी से सरल कार्य.

सरल रैखिक समीकरणों को हल करने की योजना

सबसे पहले, मैं एक बार फिर सरलतम रैखिक समीकरणों को हल करने की पूरी योजना लिखूंगा:

1. कोष्ठक का विस्तार करें, यदि कोई हो।
2. हम चरों को अलग करते हैं, अर्थात्। हम हर उस चीज़ को एक तरफ ले जाते हैं जिसमें "X" है, और हर चीज़ को बिना "X" के दूसरी तरफ ले जाते हैं।
3. हम समान शर्तें प्रस्तुत करते हैं।
4. हम हर चीज़ को "x" के गुणांक से विभाजित करते हैं।

बेशक, यह योजना हमेशा काम नहीं करती है; इसमें कुछ सूक्ष्मताएँ और तरकीबें हैं, और अब हम उन्हें जानेंगे।

सरल रैखिक समीकरणों के वास्तविक उदाहरणों को हल करना

कार्य क्रमांक 1

पहले चरण में हमें कोष्ठक खोलने की आवश्यकता है। लेकिन वे इस उदाहरण में नहीं हैं, इसलिए हम इस चरण को छोड़ देते हैं। दूसरे चरण में हमें वेरिएबल्स को अलग करने की आवश्यकता है। कृपया ध्यान दें: हम केवल व्यक्तिगत शब्दों के बारे में बात कर रहे हैं। आइए इसे लिखें:

हम बाएँ और दाएँ समान शब्द प्रस्तुत करते हैं, लेकिन यह यहाँ पहले ही किया जा चुका है। इसलिए, हम चौथे चरण पर आगे बढ़ते हैं: गुणांक से विभाजित करें:

\[\frac(6x)(6)=-\frac(72)(6)\]

तो हमें जवाब मिल गया.

कार्य क्रमांक 2

हम इस समस्या में कोष्ठक देख सकते हैं, तो आइए उनका विस्तार करें:

बाईं ओर और दाईं ओर दोनों पर हम लगभग एक ही डिज़ाइन देखते हैं, लेकिन आइए एल्गोरिथम के अनुसार कार्य करें, अर्थात। चरों को अलग करना:

यहाँ कुछ ऐसे ही हैं:

यह किन जड़ों पर काम करता है? उत्तर: किसी के लिए. इसलिए, हम लिख सकते हैं कि $x$ कोई भी संख्या है।

कार्य क्रमांक 3

तीसरा रैखिक समीकरण अधिक दिलचस्प है:

\[\left(6-x \right)+\left(12+x \right)-\left(3-2x \right)=15\]

यहां कई कोष्ठक हैं, लेकिन उन्हें किसी भी चीज़ से गुणा नहीं किया जाता है, उनके पहले बस अलग-अलग चिह्न होते हैं। आइए उन्हें तोड़ें:

हम दूसरा चरण करते हैं जो हमें पहले से ही ज्ञात है:

\[-x+x+2x=15-6-12+3\]

आइए गणित करें:

हम अंतिम चरण अपनाते हैं - हर चीज़ को "x" के गुणांक से विभाजित करते हैं:

\[\frac(2x)(x)=\frac(0)(2)\]

रैखिक समीकरणों को हल करते समय याद रखने योग्य बातें

यदि हम बहुत सरल कार्यों को नजरअंदाज करते हैं, तो मैं निम्नलिखित कहना चाहूंगा:

• जैसा कि मैंने ऊपर कहा, प्रत्येक रैखिक समीकरण का कोई हल नहीं होता - कभी-कभी कोई मूल ही नहीं होता;
• यदि जड़ें हैं भी, तो उनमें शून्य भी हो सकता है - इसमें कुछ भी गलत नहीं है।

शून्य अन्य संख्याओं के समान ही है; आपको इसके साथ किसी भी तरह का भेदभाव नहीं करना चाहिए या यह नहीं मानना ​​चाहिए कि यदि आपको शून्य मिलता है, तो आपने कुछ गलत किया है।

एक अन्य विशेषता कोष्ठक के खुलने से संबंधित है। कृपया ध्यान दें: जब उनके सामने "माइनस" होता है, तो हम उसे हटा देते हैं, लेकिन कोष्ठक में हम संकेतों को बदल देते हैं विलोम. और फिर हम इसे मानक एल्गोरिदम का उपयोग करके खोल सकते हैं: हमें वही मिलेगा जो हमने ऊपर की गणना में देखा था।

इसे समझना साधारण तथ्यइससे आप हाई स्कूल में मूर्खतापूर्ण और आक्रामक गलतियाँ करने से बच सकेंगे, जब ऐसे कार्यों को हल्के में लिया जाता है।

जटिल रैखिक समीकरणों को हल करना

आइए अधिक जटिल समीकरणों की ओर बढ़ते हैं। अब निष्पादित होने पर डिज़ाइन और अधिक जटिल हो जाएंगे विभिन्न परिवर्तनएक द्विघात फलन उत्पन्न होगा. हालाँकि, हमें इससे डरना नहीं चाहिए, क्योंकि यदि, लेखक की योजना के अनुसार, हम एक रैखिक समीकरण को हल कर रहे हैं, तो परिवर्तन प्रक्रिया के दौरान द्विघात फलन वाले सभी एकपदी निश्चित रूप से रद्द हो जाएंगे।

उदाहरण क्रमांक 1

जाहिर है, पहला कदम कोष्ठक खोलना है। आइए इसे बहुत सावधानी से करें:

आइए अब गोपनीयता पर एक नजर डालते हैं:

\[-x+6((x)^(2))-6((x)^(2))+x=-12\]

यहाँ कुछ ऐसे ही हैं:

जाहिर है, इस समीकरण का कोई समाधान नहीं है, इसलिए हम इसे उत्तर में लिखेंगे:

\[\कुछ भी नहीं\]

या कोई जड़ें नहीं हैं.

उदाहरण क्रमांक 2

हम वही क्रियाएं करते हैं. पहला कदम:

आइए एक वेरिएबल के साथ सब कुछ बाईं ओर ले जाएं, और इसके बिना - दाईं ओर:

यहाँ कुछ ऐसे ही हैं:

जाहिर है, इस रैखिक समीकरण का कोई हल नहीं है, इसलिए हम इसे इस प्रकार लिखेंगे:

\[\कुछ नहीं\],

या कोई जड़ें नहीं हैं.

समाधान की बारीकियां

दोनों समीकरण पूर्णतः हल हो गये हैं। उदाहरण के रूप में इन दो अभिव्यक्तियों का उपयोग करते हुए, हम एक बार फिर आश्वस्त हो गए कि सबसे सरल रैखिक समीकरणों में भी, सब कुछ इतना सरल नहीं हो सकता है: या तो एक, या कोई नहीं, या अनंत रूप से कई जड़ें हो सकती हैं। हमारे मामले में, हमने दो समीकरणों पर विचार किया, दोनों का कोई मूल नहीं है।

लेकिन मैं आपका ध्यान एक अन्य तथ्य की ओर आकर्षित करना चाहूंगा: कोष्ठकों के साथ कैसे काम करें और यदि उनके सामने ऋण चिह्न हो तो उन्हें कैसे खोलें। इस अभिव्यक्ति पर विचार करें:

खोलने से पहले, आपको हर चीज़ को "X" से गुणा करना होगा। कृपया ध्यान दें: गुणा करता है प्रत्येक व्यक्तिगत पद. अंदर दो पद हैं - क्रमशः, दो पद और गुणा।

और इन प्रतीत होने वाले प्राथमिक, लेकिन बहुत महत्वपूर्ण और खतरनाक परिवर्तनों के पूरा होने के बाद ही, क्या आप इस तथ्य के दृष्टिकोण से ब्रैकेट खोल सकते हैं कि इसके बाद एक ऋण चिह्न है। हाँ, हाँ: केवल अब, जब परिवर्तन पूरे हो जाते हैं, तो हमें याद आता है कि कोष्ठक के सामने एक ऋण चिह्न है, जिसका अर्थ है कि नीचे सब कुछ बस चिह्न बदलता है। उसी समय, कोष्ठक स्वयं गायब हो जाते हैं और, सबसे महत्वपूर्ण बात, सामने वाला "माइनस" भी गायब हो जाता है।

हम दूसरे समीकरण के साथ भी ऐसा ही करते हैं:

यह कोई संयोग नहीं है कि मैं इन छोटे, महत्वहीन लगने वाले तथ्यों पर ध्यान देता हूं। क्योंकि समीकरणों को हल करना हमेशा प्रारंभिक परिवर्तनों का एक क्रम होता है, जहां स्पष्ट रूप से और सक्षम रूप से सरल कार्यों को करने में असमर्थता इस तथ्य की ओर ले जाती है कि हाई स्कूल के छात्र मेरे पास आते हैं और फिर से ऐसे सरल समीकरणों को हल करना सीखते हैं।

निःसंदेह, वह दिन आएगा जब आप इन कौशलों को स्वचालितता की हद तक निखार लेंगे। अब आपको हर बार इतने सारे परिवर्तन नहीं करने पड़ेंगे; आप सब कुछ एक पंक्ति में लिखेंगे। लेकिन जब आप अभी सीख रहे हैं, तो आपको प्रत्येक क्रिया को अलग से लिखना होगा।

और भी अधिक जटिल रैखिक समीकरणों को हल करना

अब हम जो हल करने जा रहे हैं उसे शायद ही सबसे सरल कार्य कहा जा सकता है, लेकिन अर्थ वही रहता है।

कार्य क्रमांक 1

\[\left(7x+1 \right)\left(3x-1 \right)-21((x)^(2))=3\]

आइए पहले भाग के सभी तत्वों को गुणा करें:

आइए कुछ गोपनीयता बरतें:

यहाँ कुछ ऐसे ही हैं:

आइए अंतिम चरण पूरा करें:

\[\frac(-4x)(4)=\frac(4)(-4)\]

यहाँ हमारा अंतिम उत्तर है. और, इस तथ्य के बावजूद कि हल करने की प्रक्रिया में हमारे पास द्विघात फलन वाले गुणांक थे, उन्होंने एक-दूसरे को रद्द कर दिया, जो समीकरण को द्विघात नहीं बल्कि रैखिक बनाता है।

कार्य क्रमांक 2

\[\left(1-4x \right)\left(1-3x \right)=6x\left(2x-1 \right)\]

आइए पहले चरण को ध्यानपूर्वक पूरा करें: पहले ब्रैकेट के प्रत्येक तत्व को दूसरे ब्रैकेट के प्रत्येक तत्व से गुणा करें। परिवर्तनों के बाद कुल चार नए पद होने चाहिए:

आइए अब प्रत्येक पद में सावधानीपूर्वक गुणन करें:

आइए "X" वाले शब्दों को बाईं ओर और बिना वाले शब्दों को दाईं ओर ले जाएं:

\[-3x-4x+12((x)^(2))-12((x)^(2))+6x=-1\]

यहाँ समान शब्द हैं:

एक बार फिर हमें अंतिम उत्तर मिल गया है.

समाधान की बारीकियां

इन दो समीकरणों के बारे में सबसे महत्वपूर्ण नोट निम्नलिखित है: जैसे ही हम उन कोष्ठकों को गुणा करना शुरू करते हैं जिनमें एक से अधिक पद होते हैं, यह निम्नलिखित नियम के अनुसार किया जाता है: हम पहले से पहला पद लेते हैं और प्रत्येक तत्व से गुणा करते हैं दूसरा; फिर हम पहले से दूसरा तत्व लेते हैं और इसी तरह दूसरे तत्व से प्रत्येक तत्व को गुणा करते हैं। परिणामस्वरूप, हमारे पास चार पद होंगे।

बीजगणितीय योग के बारे में

इस अंतिम उदाहरण के साथ, मैं छात्रों को याद दिलाना चाहूंगा कि बीजगणितीय योग क्या है। शास्त्रीय गणित में, $1-7$ से हमारा तात्पर्य एक साधारण निर्माण से है: एक में से सात घटाएँ। बीजगणित में, इससे हमारा तात्पर्य निम्नलिखित है: संख्या "एक" में हम एक और संख्या जोड़ते हैं, जिसका नाम है "शून्य सात"। इस प्रकार एक बीजगणितीय योग एक सामान्य अंकगणितीय योग से भिन्न होता है।

जैसे ही, सभी परिवर्तनों, प्रत्येक जोड़ और गुणा को निष्पादित करते समय, आपको ऊपर वर्णित संरचनाओं के समान संरचनाएं दिखाई देने लगती हैं, तो आपको बहुपद और समीकरणों के साथ काम करते समय बीजगणित में कोई समस्या नहीं होगी।

अंत में, आइए कुछ और उदाहरण देखें जो हमारे द्वारा अभी देखे गए से भी अधिक जटिल होंगे, और उन्हें हल करने के लिए हमें अपने मानक एल्गोरिदम को थोड़ा विस्तारित करना होगा।

भिन्न वाले समीकरणों को हल करना

ऐसे कार्यों को हल करने के लिए हमें अपने एल्गोरिदम में एक और कदम जोड़ना होगा। लेकिन पहले, मैं आपको हमारे एल्गोरिदम की याद दिला दूं:

1. कोष्ठक खोलना।
2. अलग चर.
3. समान लाओ.
4. अनुपात से विभाजित करें.

अफसोस, यह अद्भुत एल्गोरिदम, अपनी सभी प्रभावशीलता के बावजूद, पूरी तरह से उपयुक्त नहीं साबित होता है जब हमारे सामने भिन्न होते हैं। और जो हम नीचे देखेंगे, उसमें दोनों समीकरणों में बाएँ और दाएँ दोनों तरफ एक भिन्न है।

इस मामले में कैसे काम करें? हाँ, यह बहुत आसान है! ऐसा करने के लिए, आपको एल्गोरिदम में एक और कदम जोड़ने की आवश्यकता है, जिसे पहली क्रिया से पहले और बाद में दोनों किया जा सकता है, अर्थात् भिन्नों से छुटकारा पाना। तो एल्गोरिथ्म इस प्रकार होगा:

1. भिन्नों से छुटकारा पाएं.
2. कोष्ठक खोलना।
3. अलग चर.
4. समान लाओ.
5. अनुपात से विभाजित करें.

"भिन्नों से छुटकारा पाने" का क्या मतलब है? और यह पहले मानक चरण के बाद और पहले दोनों समय क्यों किया जा सकता है? वास्तव में, हमारे मामले में, सभी भिन्न अपने हर में संख्यात्मक हैं, अर्थात। हर जगह हर एक संख्या ही है. इसलिए, यदि हम समीकरण के दोनों पक्षों को इस संख्या से गुणा करें, तो हमें भिन्नों से छुटकारा मिल जाएगा।

उदाहरण क्रमांक 1

\[\frac(\left(2x+1 \right)\left(2x-3 \right))(4)=((x)^(2))-1\]

आइए इस समीकरण में भिन्नों से छुटकारा पाएं:

\[\frac(\left(2x+1 \right)\left(2x-3 \right)\cdot 4)(4)=\left(((x)^(2))-1 \right)\cdot 4\]

कृपया ध्यान दें: प्रत्येक चीज़ को एक बार "चार" से गुणा किया जाता है, अर्थात। सिर्फ इसलिए कि आपके पास दो कोष्ठक हैं इसका मतलब यह नहीं है कि आपको प्रत्येक को "चार" से गुणा करना होगा। आइए लिखें:

\[\left(2x+1 \right)\left(2x-3 \right)=\left(((x)^(2))-1 \right)\cdot 4\]

अब आइए विस्तार करें:

हम चर को अलग करते हैं:

हम समान शर्तों की कमी करते हैं:

\[-4x=-1\बाएँ| :\left(-4 \right) \right.\]

\[\frac(-4x)(-4)=\frac(-1)(-4)\]

हमें अंतिम समाधान मिल गया है, आइए दूसरे समीकरण पर चलते हैं।

उदाहरण क्रमांक 2

\[\frac(\left(1-x \right)\left(1+5x \right))(5)+((x)^(2))=1\]

यहां हम वही सभी क्रियाएं करते हैं:

\[\frac(\left(1-x \right)\left(1+5x \right)\cdot 5)(5)+((x)^(2))\cdot 5=5\]

\[\frac(4x)(4)=\frac(4)(4)\]

समस्या सुलझ गई है।

वास्तव में, मैं आज आपको बस यही बताना चाहता था।

प्रमुख बिंदु

मुख्य निष्कर्ष हैं:

• रैखिक समीकरणों को हल करने के लिए एल्गोरिदम को जानें।
• कोष्ठक खोलने की क्षमता.
• यदि आप देखें तो चिंता न करें द्विघात कार्य, सबसे अधिक संभावना है, आगे के परिवर्तनों की प्रक्रिया में वे कम हो जाएंगे।
• रैखिक समीकरणों में तीन प्रकार की जड़ें होती हैं, यहां तक ​​कि सबसे सरल भी: एक एकल जड़, पूरी संख्या रेखा एक जड़ होती है, और कोई जड़ नहीं होती।

मुझे आशा है कि यह पाठ आपको संपूर्ण गणित को और अधिक समझने के लिए एक सरल, लेकिन बहुत महत्वपूर्ण विषय पर महारत हासिल करने में मदद करेगा। यदि कुछ स्पष्ट नहीं है तो साइट पर जाएं और वहां प्रस्तुत उदाहरणों को हल करें। देखते रहिए, कई और दिलचस्प चीज़ें आपका इंतज़ार कर रही हैं!

एक ऑनलाइन भिन्न कैलकुलेटर आपको सबसे सरल अंश बनाने की अनुमति देता है अंकगणितीय आपरेशनसभिन्नों के साथ: भिन्नों को जोड़ना, भिन्नों को घटाना, भिन्नों को गुणा करना, भिन्नों को विभाजित करना। गणना करने के लिए, दो भिन्नों के अंश और हर के अनुरूप फ़ील्ड भरें।

गणित में भिन्नएक संख्या एक इकाई के एक भाग या उसके कई भागों का प्रतिनिधित्व करती है।

एक सामान्य भिन्न को दो संख्याओं के रूप में लिखा जाता है, जो आमतौर पर विभाजन चिह्न को इंगित करने वाली एक क्षैतिज रेखा से अलग होती हैं। रेखा के ऊपर की संख्या को अंश कहा जाता है। रेखा के नीचे की संख्या को हर कहा जाता है। भिन्न का हर उन समान भागों की संख्या दर्शाता है जिनमें पूर्णांक विभाजित है, और भिन्न का अंशांकक पूर्णांक के इन भागों की संख्या दर्शाता है।

भिन्न नियमित या अनुचित हो सकते हैं।

• वह भिन्न जिसका अंश उसके हर से कम हो, उचित भिन्न कहलाती है।
• अनुचित भिन्न तब होती है जब भिन्न का अंश हर से बड़ा होता है।

मिश्रित भिन्न वह भिन्न है जिसे पूर्णांक और उचित भिन्न के रूप में लिखा जाता है, और इसे इस संख्या और भिन्नात्मक भाग के योग के रूप में समझा जाता है। तदनुसार, जिस भिन्न में पूर्णांक भाग नहीं होता, उसे साधारण भिन्न कहा जाता है। किसी भी मिश्रित भिन्न को अनुचित भिन्न में बदला जा सकता है।

मिश्रित भिन्न को सामान्य भिन्न में बदलने के लिए, आपको भिन्न के अंश में पूरे भाग और हर के गुणनफल को जोड़ना होगा:

सामान्य भिन्न को मिश्रित भिन्न में कैसे बदलें

अनुवाद करने के लिए सामान्य अंशमिश्रित, आपको चाहिए:

1. किसी भिन्न के अंश को उसके हर से विभाजित करें
2. विभाजन का परिणाम सम्पूर्ण भाग होगा
3. विभाग का शेष अंश-गणक होगा

भिन्न को दशमलव में कैसे बदलें

किसी भिन्न को दशमलव में बदलने के लिए, आपको उसके अंश को उसके हर से विभाजित करना होगा।

अनुवाद करने के लिए दशमलवहमेशा की तरह, आपको चाहिए:

भिन्न को प्रतिशत में कैसे बदलें

किसी सामान्य या मिश्रित अंश को प्रतिशत में बदलने के लिए, आपको इसे दशमलव अंश में बदलना होगा और 100 से गुणा करना होगा।

प्रतिशत को भिन्न में कैसे बदलें

प्रतिशत को भिन्न में बदलने के लिए, आपको प्रतिशत से एक दशमलव अंश प्राप्त करना होगा (100 से विभाजित करना), फिर परिणामी दशमलव अंश को एक साधारण भिन्न में बदलना होगा।

भिन्न जोड़ना

दो भिन्नों को जोड़ने का एल्गोरिदम इस प्रकार है:

1. भिन्नों को उनके अंशों को जोड़कर जोड़ना।

भिन्नों को घटाना

दो भिन्नों को घटाने के लिए एल्गोरिदम:

1. अनुवाद मिश्रित अंशसामान्य में (पूरे भाग से छुटकारा पाएं)।
2. भिन्नों को परिवर्तित करें आम विभाजक. ऐसा करने के लिए, आपको पहले अंश के अंश और हर को दूसरे अंश के हर से गुणा करना होगा, और दूसरे अंश के अंश और हर को पहले अंश के हर से गुणा करना होगा।
3. पहले भिन्न के अंश में से दूसरे भिन्न के अंश को घटाकर एक भिन्न को दूसरे भिन्न से घटाएँ।
4. अंश और हर का सबसे बड़ा सामान्य भाजक (जीसीडी) ढूंढें और अंश और हर को जीसीडी से विभाजित करके भिन्न को कम करें।
5. यदि अंतिम भिन्न का अंश हर से बड़ा है, तो पूरे भाग का चयन करें।

भिन्नों को गुणा करना

दो भिन्नों को गुणा करने के लिए एल्गोरिदम:

1. मिश्रित भिन्नों को साधारण भिन्नों में बदलें (पूरे भाग से छुटकारा पाएं)।
2. अंश और हर का सबसे बड़ा सामान्य भाजक (जीसीडी) ढूंढें और अंश और हर को जीसीडी से विभाजित करके भिन्न को कम करें।
3. यदि अंतिम भिन्न का अंश हर से बड़ा है, तो पूरे भाग का चयन करें।

भिन्नों का विभाजन

दो भिन्नों को विभाजित करने के लिए एल्गोरिदम:

1. मिश्रित भिन्नों को साधारण भिन्नों में बदलें (पूरे भाग से छुटकारा पाएं)।
2. भिन्नों को विभाजित करने के लिए, आपको दूसरे भिन्न को उसके अंश और हर की अदला-बदली करके बदलना होगा, और फिर भिन्नों को गुणा करना होगा।
3. पहले भिन्न के अंश को दूसरे भिन्न के अंश से और पहले भिन्न के हर को दूसरे भिन्न के हर से गुणा करें।
4. अंश और हर का सबसे बड़ा सामान्य भाजक (जीसीडी) ढूंढें और अंश और हर को जीसीडी से विभाजित करके भिन्न को कम करें।
5. यदि अंतिम भिन्न का अंश हर से बड़ा है, तो पूरे भाग का चयन करें।

ऑनलाइन कैलकुलेटर और कन्वर्टर्स:

एक अज्ञात के साथ एक समीकरण, जो कोष्ठक खोलने और समान पदों को लाने के बाद, रूप लेता है

कुल्हाड़ी + बी = 0, जहाँ a और b मनमानी संख्याएँ हैं, कहलाती हैं रेखीय समीकरण एक अज्ञात के साथ. आज हम यह पता लगाएंगे कि इन रैखिक समीकरणों को कैसे हल किया जाए।

उदाहरण के लिए, सभी समीकरण:

2x + 3= 7 – 0.5x; 0.3x = 0; x/2 + 3 = 1/2 (x – 2) - रैखिक।

अज्ञात का वह मान जो समीकरण को वास्तविक समानता में बदल देता है, कहलाता है फ़ैसला या समीकरण की जड़ .

उदाहरण के लिए, यदि समीकरण 3x + 7 = 13 में अज्ञात x के स्थान पर हम संख्या 2 रखते हैं, तो हमें सही समानता 3 2 +7 = 13 प्राप्त होती है। इसका मतलब है कि मान x = 2 समाधान या मूल है समीकरण का.

और मान x = 3 समीकरण 3x + 7 = 13 को वास्तविक समानता में नहीं बदलता है, क्योंकि 3 2 +7 ≠ 13. इसका मतलब यह है कि मान x = 3 कोई समाधान या समीकरण का मूल नहीं है।

किसी भी रैखिक समीकरण को हल करने से प्रपत्र के समीकरणों को हल करना कम हो जाता है

कुल्हाड़ी + बी = 0.

आइए समीकरण के बाईं ओर से मुक्त पद को दाईं ओर ले जाएं, b के सामने के चिह्न को विपरीत दिशा में बदलते हुए, हमें मिलता है

यदि a ≠ 0, तो x = ‒ b/a .

उदाहरण 1। समीकरण 3x + 2 =11 को हल करें.

आइए 2 को समीकरण के बाईं ओर से दाईं ओर ले जाएं, 2 के सामने के चिह्न को विपरीत दिशा में बदलते हुए, हमें मिलता है
3x = 11 – 2.

तो चलिए घटाव करते हैं
3x = 9.

x ज्ञात करने के लिए, आपको गुणनफल को किसी ज्ञात कारक से विभाजित करना होगा, अर्थात
एक्स = 9:3.

इसका अर्थ यह है कि मान x = 3 समीकरण का हल या मूल है।

उत्तर: एक्स = 3.

यदि a = 0 और b = 0, तो हमें समीकरण 0x = 0 मिलता है। इस समीकरण के अनंत रूप से कई समाधान हैं, क्योंकि जब हम किसी संख्या को 0 से गुणा करते हैं तो हमें 0 मिलता है, लेकिन b भी 0 के बराबर होता है। इस समीकरण का समाधान कोई भी संख्या है।

उदाहरण 2.समीकरण 5(x – 3) + 2 = 3 (x – 4) + 2x ‒ 1 को हल करें।

आइए कोष्ठक का विस्तार करें:
5x – 15 + 2 = 3x – 12 + 2x ‒ 1.

5x – 3x ‒ 2x = – 12 ‒ 1 + 15 ‒ 2.

यहां कुछ समान शब्द दिए गए हैं:
0x = 0.

उत्तर: x - कोई भी संख्या.

यदि a = 0 और b ≠ 0, तो हमें समीकरण 0x = - b प्राप्त होता है। इस समीकरण का कोई हल नहीं है, क्योंकि जब हम किसी संख्या को 0 से गुणा करते हैं तो हमें 0 मिलता है, लेकिन b ≠ 0 मिलता है।

उदाहरण 3.समीकरण x + 8 = x + 5 को हल करें।

आइए बायीं तरफ अज्ञात वाले शब्दों को और दायीं तरफ मुक्त शब्दों को समूहित करें:
एक्स - एक्स = 5 - 8.

यहां कुछ समान शब्द दिए गए हैं:
0х = ‒3.

उत्तर: कोई समाधान नहीं.

पर आकृति 1 एक रैखिक समीकरण को हल करने के लिए एक आरेख दिखाता है

आइए एक चर वाले समीकरणों को हल करने के लिए एक सामान्य योजना बनाएं। आइए उदाहरण 4 के समाधान पर विचार करें।

उदाहरण 4. मान लीजिए हमें समीकरण हल करना है

1) समीकरण के सभी पदों को 12 के बराबर हर के लघुत्तम समापवर्त्य से गुणा करें।

2) कटौती के बाद हमें मिलता है
4 (x – 4) + 3 2 (x + 1) ‒ 12 = 6 5 (x – 3) + 24x – 2 (11x + 43)

3) अज्ञात और मुक्त पदों वाले शब्दों को अलग करने के लिए, कोष्ठक खोलें:
4x – 16 + 6x + 6 – 12 = 30x – 90 + 24x – 22x – 86.

4) आइए हम एक भाग में अज्ञात वाले पदों को समूहित करें, और दूसरे भाग में मुक्त पदों को समूहित करें:
4x + 6x – 30x – 24x + 22x = ‒ 90 – 86 + 16 – 6 + 12.

5) आइए हम समान शब्द प्रस्तुत करें:
- 22х = - 154.

6) – 22 से भाग देने पर हमें प्राप्त होता है
एक्स = 7.

जैसा कि आप देख सकते हैं, समीकरण का मूल सात है।

आम तौर पर ऐसा निम्नलिखित योजना का उपयोग करके समीकरणों को हल किया जा सकता है:

ए) समीकरण को उसके पूर्णांक रूप में लाएँ;

बी) कोष्ठक खोलें;

ग) समीकरण के एक भाग में अज्ञात और दूसरे भाग में मुक्त पदों वाले पदों को समूहित करें;

घ) समान सदस्य लाएँ;

ई) aх = b के रूप का एक समीकरण हल करें, जो समान पदों को लाने के बाद प्राप्त किया गया था।

हालाँकि, यह योजना हर समीकरण के लिए आवश्यक नहीं है। कई सरल समीकरणों को हल करते समय, आपको पहले से नहीं, बल्कि दूसरे से शुरुआत करनी होगी ( उदाहरण। 2), तीसरा ( उदाहरण। 13) और यहां तक ​​कि पांचवें चरण से भी, जैसा कि उदाहरण 5 में है।

उदाहरण 5.समीकरण 2x = 1/4 को हल करें।

अज्ञात ज्ञात कीजिए x = 1/4: 2,
एक्स = 1/8 .

आइए मुख्य राज्य परीक्षा में पाए गए कुछ रैखिक समीकरणों को हल करने पर नज़र डालें।

उदाहरण 6.समीकरण 2 (x + 3) = 5 - 6x को हल करें।

2x + 6 = 5 – 6x

2x + 6x = 5 – 6

उत्तर:- 0.125

उदाहरण 7.समीकरण हल करें - 6 (5 - 3x) = 8x - 7.

– 30 + 18x = 8x – 7

18x – 8x = – 7 +30

उत्तर: 2.3

उदाहरण 8. प्रश्न हल करें

3(3x – 4) = 4 7x + 24

9x – 12 = 28x + 24

9x – 28x = 24 + 12

उदाहरण 9.यदि f (x + 2) = 3 7 है तो f(6) ज्ञात कीजिए

समाधान

चूँकि हमें f(6) खोजने की आवश्यकता है, और हम f (x + 2) जानते हैं,
तो x + 2 = 6.

हम रैखिक समीकरण x + 2 = 6 को हल करते हैं,
हमें x = 6 – 2, x = 4 मिलता है।

यदि x = 4 है तो
एफ(6) = 3 7-4 = 3 3 = 27

उत्तर: 27.

यदि आपके पास अभी भी प्रश्न हैं या आप समीकरणों को हल करने को अधिक अच्छी तरह से समझना चाहते हैं, तो अनुसूची में मेरे पाठों के लिए साइन अप करें। मुझे आपकी मदद करने में खुशी होगी!

ट्यूटरऑनलाइन हमारी ट्यूटर ओल्गा अलेक्जेंड्रोवना का एक नया वीडियो पाठ देखने की भी सिफारिश करता है, जो आपको रैखिक समीकरणों और अन्य दोनों को समझने में मदद करेगा।

वेबसाइट, सामग्री को पूर्ण या आंशिक रूप से कॉपी करते समय, स्रोत के लिंक की आवश्यकता होती है।

अपरिमेय समीकरण क्या हैं और उन्हें कैसे हल करें?

वे समीकरण जिनमें चर मूलांक चिह्न के अंतर्गत या भिन्नात्मक घात तक बढ़ने के चिह्न के अंतर्गत समाहित होता है, कहलाते हैं तर्कहीन. जब हम भिन्नात्मक शक्तियों से निपटते हैं, तो हम समीकरण को हल करने के लिए कई गणितीय संक्रियाओं से खुद को वंचित कर लेते हैं, इसलिए अपरिमेय समीकरणों को एक विशेष तरीके से हल किया जाता है।

अपरिमेय समीकरणों को आमतौर पर समीकरण के दोनों पक्षों को समान घात तक बढ़ाकर हल किया जाता है। इस मामले में, समीकरण के दोनों पक्षों को एक ही विषम घात तक बढ़ाना समीकरण का एक समतुल्य परिवर्तन है, और इसे एक सम घात तक बढ़ाना एक असमान परिवर्तन है। यह अंतर एक घात तक बढ़ाने की ऐसी विशेषताओं के कारण प्राप्त होता है, जैसे कि यदि एक सम घात तक बढ़ाया जाए, तो नकारात्मक मान"भाड़ में जाओ।"

एक अतार्किक समीकरण के दोनों पक्षों को एक शक्ति तक बढ़ाने का उद्देश्य "अतार्किकता" से छुटकारा पाने की इच्छा है। इस प्रकार, हमें अपरिमेय समीकरण के दोनों पक्षों को इस हद तक ऊपर उठाने की आवश्यकता है कि समीकरण के दोनों पक्षों की सभी भिन्नात्मक घातें पूर्णांकों में बदल जाएँ। जिसके बाद आप इस समीकरण के समाधान की तलाश कर सकते हैं, जो अपरिमेय समीकरण के समाधानों के साथ मेल खाएगा, इस अंतर के साथ कि सम घात तक बढ़ने की स्थिति में, चिह्न खो जाता है और अंतिम समाधान के लिए सत्यापन की आवश्यकता होगी और नहीं सभी उपयुक्त होंगे.

इस प्रकार, मुख्य कठिनाई समीकरण के दोनों पक्षों को समान सम घात तक बढ़ाने से जुड़ी है - परिवर्तन की असमानता के कारण, बाहरी जड़ें दिखाई दे सकती हैं। इसलिए, सभी पाई गई जड़ों की जांच करना आवश्यक है। जो लोग किसी अपरिमेय समीकरण को हल करते हैं वे अक्सर पाए गए मूलों की जांच करना भूल जाते हैं। यह भी हमेशा स्पष्ट नहीं होता है कि अतार्किकता से छुटकारा पाने और उसे हल करने के लिए किसी अतार्किक समीकरण को किस हद तक बढ़ाया जाना चाहिए। हमारा स्मार्ट कैलकुलेटर विशेष रूप से अतार्किक समीकरणों को हल करने और स्वचालित रूप से सभी जड़ों की जांच करने के लिए बनाया गया था, जो आपको भूलने की बीमारी से बचाएगा।

निःशुल्क ऑनलाइन अपरिमेय समीकरण कैलकुलेटर

हमारा निःशुल्क सॉल्वर आपको किसी भी जटिलता के अतार्किक समीकरण को कुछ ही सेकंड में ऑनलाइन हल करने की अनुमति देगा। आपको बस अपना डेटा कैलकुलेटर में दर्ज करना है। आप हमारी वेबसाइट पर यह भी जान सकते हैं कि समीकरण को कैसे हल किया जाए। और यदि आपके पास अभी भी प्रश्न हैं, तो आप उन्हें हमारे VKontakte समूह में पूछ सकते हैं।

सेवा का उद्देश्य. मैट्रिक्स कैलकुलेटर को मैट्रिक्स विधि का उपयोग करके रैखिक समीकरणों की प्रणालियों को हल करने के लिए डिज़ाइन किया गया है (समान समस्याओं को हल करने का उदाहरण देखें)।

निर्देश। के लिए ऑनलाइन समाधानसमीकरण के प्रकार का चयन करना और संबंधित आव्यूहों का आयाम निर्धारित करना आवश्यक है। जहां ए, बी, सी निर्दिष्ट मैट्रिक्स हैं, एक्स वांछित मैट्रिक्स है। फॉर्म (1), (2) और (3) के मैट्रिक्स समीकरण व्युत्क्रम मैट्रिक्स ए -1 के माध्यम से हल किए जाते हैं। यदि व्यंजक A·X - B = C दिया गया है, तो पहले आव्यूह C + B को जोड़ना और व्यंजक A·X = D के लिए एक समाधान खोजना आवश्यक है, जहां D = C + B. यदि अभिव्यक्ति A*X = B 2 दी गई है, तो मैट्रिक्स B को पहले वर्गित किया जाना चाहिए।

मैट्रिसेस पर बुनियादी संचालन से खुद को परिचित करने की भी सिफारिश की जाती है।

उदाहरण क्रमांक 1. व्यायाम. मैट्रिक्स समीकरण का हल खोजें
समाधान. आइए निरूपित करें:
फिर मैट्रिक्स समीकरण इस रूप में लिखा जाएगा: A·X·B = C.
मैट्रिक्स A का निर्धारक detA=-1 के बराबर है
चूँकि A एक गैर-एकवचन मैट्रिक्स है, इसलिए एक व्युत्क्रम मैट्रिक्स A -1 है। समीकरण के बाईं ओर के दोनों पक्षों को A -1 से गुणा करें: इस समीकरण के बाईं ओर के दोनों पक्षों को A -1 से और दाईं ओर के B -1 से गुणा करें: A -1 ·A·X·B·B -1 = ए -1 ·सी·बी -1 . चूँकि A A -1 = B B -1 = E और E X = X E = X, तो X = A -1 C B -1

उलटा मैट्रिक्सए-1:
आइए व्युत्क्रम मैट्रिक्स B-1 खोजें।
ट्रांसपोज़्ड मैट्रिक्स बी टी:
उलटा मैट्रिक्स बी -1:
हम सूत्र का उपयोग करके मैट्रिक्स एक्स की तलाश करते हैं: एक्स = ए -1 ·सी·बी -1

उत्तर:

उदाहरण क्रमांक 2. व्यायाम।मैट्रिक्स समीकरण हल करें
समाधान. आइए निरूपित करें:
फिर मैट्रिक्स समीकरण इस रूप में लिखा जाएगा: A·X = B.
मैट्रिक्स A का निर्धारक detA=0 है
चूँकि A एक विलक्षण मैट्रिक्स है (निर्धारक 0 है), इसलिए समीकरण का कोई हल नहीं है।

उदाहरण संख्या 3. व्यायाम। मैट्रिक्स समीकरण का हल खोजें
समाधान. आइए निरूपित करें:
फिर मैट्रिक्स समीकरण इस रूप में लिखा जाएगा: X A = B.
मैट्रिक्स A का निर्धारक detA=-60 है
चूँकि A एक गैर-एकवचन मैट्रिक्स है, इसलिए एक व्युत्क्रम मैट्रिक्स A -1 है। आइए समीकरण के दोनों पक्षों को दाईं ओर A -1 से गुणा करें: X A A -1 = B A -1, जहां से हमें पता चलता है कि X = B A -1
आइए व्युत्क्रम मैट्रिक्स A -1 खोजें।
ट्रांसपोज़्ड मैट्रिक्स ए टी: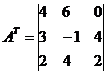
उलटा मैट्रिक्स ए -1:
हम सूत्र का उपयोग करके मैट्रिक्स एक्स की तलाश करते हैं: एक्स = बी ए -1


उत्तर: >