ஒரு கார்ட்டீசியன் செவ்வக ஒருங்கிணைப்பு அமைப்பு Oxy மற்றும் சில வரி L விமானத்தில் கொடுக்கப்பட வேண்டும் .

வரையறை. சமன்பாடு F(x;y)=0 (1)அழைக்கப்பட்டது வரி சமன்பாடுஎல்(ஒரு கொடுக்கப்பட்ட ஒருங்கிணைப்பு அமைப்புடன் தொடர்புடையது) இந்த சமன்பாடு L கோட்டில் இருக்கும் எந்தப் புள்ளியின் x மற்றும் y ஆயத்தொகுப்புகளை திருப்திப்படுத்துகிறது மற்றும் L கோட்டில் இல்லாத எந்தப் புள்ளியின் x மற்றும் y ஆயத்தொகுப்புகளையும் திருப்திப்படுத்தவில்லை என்றால்.

அந்த. விமானத்தில் வரிபுள்ளிகளின் இருப்பிடம் (M(x;y)) அதன் ஒருங்கிணைப்புகள் சமன்பாட்டை (1) பூர்த்தி செய்கின்றன.

சமன்பாடு (1) எல் வரியை வரையறுக்கிறது.

உதாரணமாக. வட்டச் சமன்பாடு.

வட்டம்- கொடுக்கப்பட்ட புள்ளி M 0 (x 0, y 0) க்கு சமமான புள்ளிகளின் தொகுப்பு.

புள்ளி M 0 (x 0, y 0) - வட்ட மையம்.

வட்டத்தில் இருக்கும் எந்தப் புள்ளிக்கும் M(x; y) தூரம் MM 0 =R (R=const)

எம்.எம் 0 ==ஆர்

(x-x 0 ) 2 +(y-y 0 ) 2 =ஆர் 2 –(2) – M 0 (x 0, y 0) புள்ளியை மையமாகக் கொண்ட ஆரம் R வட்டத்தின் சமன்பாடு.

அளவுகோல் சமன்பாடு.

L கோட்டின் புள்ளிகளின் x மற்றும் y ஆயங்களை t அளவுருவைப் பயன்படுத்தி வெளிப்படுத்தலாம்:

(3) - டிஎஸ்சியில் கோட்டின் அளவுரு சமன்பாடு

இதில் (t) மற்றும் (t) ஆகிய செயல்பாடுகள் t அளவுருவைப் பொறுத்து தொடர்ச்சியாக இருக்கும் (இந்த அளவுருவின் குறிப்பிட்ட வரம்பில்).

சமன்பாடு (3) இலிருந்து t அளவுருவை நீக்கி, சமன்பாடு (1) ஐப் பெறுகிறோம்.

L கோடு ஒரு பொருள் புள்ளியால் பயணிக்கும் பாதையாகக் கருதுவோம், ஒரு குறிப்பிட்ட சட்டத்தின்படி தொடர்ந்து நகரும். t மாறி சில ஆரம்ப தருணத்திலிருந்து கணக்கிடப்பட்ட நேரத்தைக் குறிக்கட்டும். பின்னர் சில தொடர்ச்சியான செயல்பாடுகள் x=(t) மற்றும் y=(t) நேர t என நகரும் புள்ளியின் x மற்றும் y ஒருங்கிணைப்புகளின் பணி இயக்க விதியின் பணியாகும்.

உதாரணமாக. மூலத்தை மையமாகக் கொண்ட ஆரம் r>0 வட்டத்திற்கான அளவுரு சமன்பாட்டைப் பெறுவோம். M(x, y) இந்த வட்டத்தின் தன்னிச்சையான புள்ளியாக இருக்கட்டும், மற்றும் t என்பது ஆரம் திசையன் மற்றும் ஆக்ஸ் அச்சுக்கு இடையே உள்ள கோணம், எதிரெதிர் திசையில் கணக்கிடப்படும்.

பிறகு x=r cos x y=r sin t. (4)

சமன்பாடுகள் (4) என்பது கருதப்படும் வட்டத்தின் அளவுரு சமன்பாடுகள். அளவுரு t எந்த மதிப்பையும் எடுக்கலாம், ஆனால் புள்ளி M(x, y) வட்டத்தை ஒருமுறை சுற்றி வர, அளவுரு மாற்ற பகுதி 0t2 அரை-பிரிவுக்கு வரம்பிடப்பட்டுள்ளது.

சதுரம் மற்றும் சமன்பாடுகளைச் சேர்ப்பது (4), வட்டத்தின் பொதுவான சமன்பாட்டைப் பெறுகிறோம் (2).

2. துருவ ஒருங்கிணைப்பு அமைப்பு (psc).

விமானத்தில் L அச்சை தேர்வு செய்வோம் ( துருவ அச்சு) மற்றும் இந்த அச்சின் புள்ளியை தீர்மானிக்கவும் О ( கம்பம்) விமானத்தின் எந்தப் புள்ளியும் துருவ ஆயத்தொலைவுகளான ρ மற்றும் φ மூலம் தனித்துவமாக வரையறுக்கப்படுகிறது.

ρ – துருவ ஆரம், புள்ளி M இலிருந்து துருவ O (ρ≥0) க்கு உள்ள தூரத்திற்கு சமம்;

φ – மூலையில்திசையன் திசைக்கு இடையே ஓம்மற்றும் எல் அச்சு ( துருவ கோணம்). எம்(ρ ; φ )

UCS இல் வரி சமன்பாடுஎழுத முடியும்:

ρ=f(φ) (5) PCS இல் வெளிப்படையான வரி சமன்பாடு

F=(ρ; φ) (6) PCS இல் மறைமுக வரி சமன்பாடு

ஒரு புள்ளியின் கார்ட்டீசியன் மற்றும் துருவ ஒருங்கிணைப்புகளுக்கு இடையிலான உறவு.

(x; y) (ρ ; φ ) OMA முக்கோணத்திலிருந்து:

tg φ=(கோணத்தின் மறுசீரமைப்புφ நன்கு அறியப்பட்ட படிதொடுகோடு உற்பத்தி செய்யப்படுகிறதுM புள்ளி எந்த நால்பகுதியில் அமைந்துள்ளது என்பதை கணக்கில் எடுத்துக்கொள்வது).(ρ ; φ )(x; y). x=ρcos φ,y= ρsin φ

உதாரணமாக . M(3;4) மற்றும் P(1;-1) புள்ளிகளின் துருவ ஆயத்தொலைவுகளைக் கண்டறியவும்.

M:=5, φ=arctg (4/3). Pக்கு: ρ=; φ=Π+arctg(-1)=3Π/4.

தட்டையான கோடுகளின் வகைப்பாடு.

வரையறை 1.வரி அழைக்கப்படுகிறது இயற்கணிதம்,சில கார்ட்டீசியன் செவ்வக ஒருங்கிணைப்பு அமைப்பில் இருந்தால், அது F(x;y)=0 (1) சமன்பாட்டால் வரையறுக்கப்பட்டால், இதில் F(x;y) என்பது இயற்கணித பல்லுறுப்புக்கோவை ஆகும்.

வரையறை 2.இயற்கணிதம் அல்லாத எந்த வரியும் அழைக்கப்படுகிறது மீறிய.

வரையறை 3. இயற்கணிதக் கோடு அழைக்கப்படுகிறது ஒழுங்கு வரிn, சில கார்ட்டீசியன் செவ்வக ஒருங்கிணைப்பு அமைப்பில் இந்தக் கோடு சமன்பாடு (1) மூலம் தீர்மானிக்கப்படுகிறது, இதில் F(x;y) சார்பு nவது பட்டத்தின் இயற்கணித பல்லுறுப்புக்கோவை ஆகும்.

இவ்வாறு, n வது வரிசையின் ஒரு கோடு என்பது சில கார்ட்டீசியன் செவ்வக அமைப்பில் இரண்டு அறியப்படாதவைகளுடன் பட்டம் n இன் இயற்கணித சமன்பாட்டின் மூலம் வரையறுக்கப்பட்ட ஒரு கோடு ஆகும்.

பின்வரும் தேற்றம் 1,2,3 வரையறைகளின் சரியான தன்மையை நிறுவ உதவுகிறது.

தேற்றம்(பக். 107 இல் ஆவணம்). சில கார்ட்டீசியன் செவ்வக ஒருங்கிணைப்பு அமைப்பில் உள்ள ஒரு கோடு n பட்டத்தின் இயற்கணித சமன்பாட்டால் தீர்மானிக்கப்பட்டால், வேறு எந்த கார்ட்டீசியன் செவ்வக ஒருங்கிணைப்பு அமைப்பிலும் உள்ள இந்த வரி அதே டிகிரி n இன் இயற்கணித சமன்பாட்டால் தீர்மானிக்கப்படுகிறது.

புள்ளிகளின் இருப்பிடமாக ஒரு கோட்டின் சமன்பாடு. ஒரு நேர் கோட்டின் பல்வேறு வகையான சமன்பாடுகள். ஒரு நேர்கோட்டின் பொதுவான சமன்பாடு பற்றிய ஆய்வு. அதன் சமன்பாட்டின் படி ஒரு நேர்கோட்டின் கட்டுமானம்

வரி சமன்பாடுமாறிகள் கொண்ட சமன்பாடு என்று அழைக்கப்படுகிறது எக்ஸ்மற்றும் ஒய், இந்த வரியின் எந்தப் புள்ளியின் ஆயத்தொலைவுகளாலும் அவற்றால் மட்டுமே திருப்தி அடையும்.

வரி சமன்பாட்டில் சேர்க்கப்பட்டுள்ள மாறிகள் எக்ஸ்மற்றும் ஒய்தற்போதைய ஆயத்தொலைவுகள் என்றும், எழுத்துநிலை மாறிலிகள் அளவுருக்கள் என்றும் அழைக்கப்படுகின்றன.

ஒரு கோட்டின் சமன்பாட்டை ஒரே சொத்தை கொண்ட புள்ளிகளின் இருப்பிடமாக உருவாக்க, உங்களுக்கு இது தேவை:

1) தன்னிச்சையான (தற்போதைய) புள்ளியை எடுத்துக் கொள்ளுங்கள் எம்(எக்ஸ், ஒய்) கோடுகள்;
2) அனைத்து புள்ளிகளின் பொதுவான சொத்தை சமத்துவத்தால் எழுதுங்கள் எம்கோடுகள்;
3) இந்த சமத்துவத்தில் சேர்க்கப்பட்டுள்ள பிரிவுகள் (மற்றும் கோணங்கள்) புள்ளியின் தற்போதைய ஆயங்களின் அடிப்படையில் வெளிப்படுத்தப்படுகின்றன எம்(எக்ஸ், ஒய்) மற்றும் பணியில் உள்ள தரவு மூலம்.

செவ்வக ஆயங்களில், ஒரு விமானத்தில் ஒரு நேர் கோட்டின் சமன்பாடு பின்வரும் வடிவங்களில் ஒன்றில் கொடுக்கப்பட்டுள்ளது:

1. சாய்வுடன் கூடிய நேர்கோட்டின் சமன்பாடு

ஒய் = kx + பி, (1)

எங்கே கே- நேர்கோட்டின் சாய்வு, அதாவது நேர்கோடு அச்சின் நேர் திசையுடன் உருவாகும் கோணத்தின் தொடுகோடு எருது, மற்றும் இந்த கோணம் அச்சில் இருந்து அளவிடப்படுகிறது எருதுநேர்கோட்டில் எதிரெதிர் திசையில், பி- y- அச்சில் ஒரு நேர் கோட்டால் துண்டிக்கப்பட்ட பிரிவின் மதிப்பு. மணிக்கு பி= 0 சமன்பாடு (1) வடிவம் கொண்டது ஒய் = kxமற்றும் தொடர்புடைய வரி தோற்றம் வழியாக செல்கிறது.

சமன்பாடு (1) அச்சுக்கு செங்குத்தாக இல்லாத விமானத்தில் எந்த நேர்கோட்டையும் வரையறுக்கப் பயன்படுகிறது. எருது.

தற்போதைய ஒருங்கிணைப்புடன் ஒப்பிடும்போது சாய்வுடன் கூடிய நேர்கோட்டின் சமன்பாடு அனுமதிக்கப்படுகிறது ஒய்.

2. ஒரு நேர்கோட்டின் பொதுவான சமன்பாடு

கோடாரி + மூலம் + சி = 0. (2)

ஒரு நேர் கோட்டின் பொதுவான சமன்பாட்டின் குறிப்பிட்ட வழக்குகள்.

1. ஒரு விமானத்தில் ஒரு கோட்டின் சமன்பாடு

உங்களுக்குத் தெரியும், விமானத்தின் எந்த புள்ளியும் எந்த ஒருங்கிணைப்பு அமைப்பிலும் இரண்டு ஆயங்களால் தீர்மானிக்கப்படுகிறது. அடிப்படை மற்றும் தோற்றத்தின் தேர்வைப் பொறுத்து ஒருங்கிணைப்பு அமைப்புகள் வேறுபட்டிருக்கலாம்.

வரையறை. கோடு சமன்பாடு என்பது இந்த வரியை உருவாக்கும் புள்ளிகளின் ஆயத்தொலைவுகளுக்கு இடையே உள்ள விகிதம் y \u003d f (x) ஆகும்.

வரி சமன்பாட்டை ஒரு அளவுரு வழியில் வெளிப்படுத்தலாம் என்பதை நினைவில் கொள்க, அதாவது, ஒவ்வொரு புள்ளியின் ஒவ்வொரு ஒருங்கிணைப்பும் சில சுயாதீன அளவுரு t மூலம் வெளிப்படுத்தப்படுகிறது. ஒரு பொதுவான உதாரணம் ஒரு நகரும் புள்ளியின் பாதை. இந்த வழக்கில், நேரம் ஒரு அளவுருவின் பாத்திரத்தை வகிக்கிறது.

2. ஒரு விமானத்தில் ஒரு நேர்கோட்டின் சமன்பாடு

வரையறை. விமானத்தில் உள்ள எந்த நேர்கோட்டையும் Ax + By + C = 0 என்ற முதல் வரிசை சமன்பாட்டின் மூலம் வழங்க முடியும், மேலும் A , B ஆகியவை ஒரே நேரத்தில் பூஜ்ஜியத்திற்கு சமமாக இருக்காது, அதாவது.

A 2 + B 2 ≠ 0 . இந்த முதல்-வரிசை சமன்பாடு ஒரு நேர்கோட்டின் பொது சமன்பாடு என்று அழைக்கப்படுகிறது.

IN A, B மற்றும் C மாறிலிகளின் மதிப்புகளைப் பொறுத்து, பின்வரும் சிறப்பு நிகழ்வுகள் சாத்தியமாகும்:

- கோடு தோற்றம் வழியாக செல்கிறது

C \u003d 0, A ≠ 0, B ≠ 0 ( By + C \u003d 0) - கோடு ஆக்ஸ் அச்சுக்கு இணையாக உள்ளது

B = 0, A ≠ 0, C ≠ 0(Ax + C = 0) - கோடு Oy அச்சுக்கு இணையாக உள்ளது

B = C = 0, A ≠ 0 - கோடு Oy அச்சுடன் ஒத்துப்போகிறது

A = C = 0, B ≠ 0 - கோடு ஆக்ஸ் அச்சுடன் ஒத்துப்போகிறது

ஒரு நேர்கோட்டின் சமன்பாடு கொடுக்கப்பட்ட ஆரம்ப நிலைகளைப் பொறுத்து பல்வேறு வடிவங்களில் வழங்கப்படலாம்.

3. ஒரு புள்ளி மற்றும் ஒரு சாதாரண திசையன் தொடர்பாக ஒரு நேர்கோட்டின் சமன்பாடு

வரையறை. கார்ட்டீசியன் செவ்வக ஒருங்கிணைப்பு அமைப்பில், கூறுகளைக் கொண்ட ஒரு திசையன் (A, B) சமன்பாட்டால் கொடுக்கப்பட்ட கோட்டிற்கு செங்குத்தாக உள்ளது.

Ax + By + C = 0.

உதாரணமாக. திசையன் n (3, - 1) க்கு செங்குத்தாக А(1,2) புள்ளி வழியாக செல்லும் நேர்கோட்டின் சமன்பாட்டைக் கண்டறியவும்.

ஒரு நேர் கோட்டின் சமன்பாட்டை A=3 மற்றும் B=-1க்கு எழுதவும்: 3x - y + C = 0 . குணகம் கண்டுபிடிக்க

கொடுக்கப்பட்ட புள்ளி A இன் ஆயத்தொலைவுகளை விளைந்த வெளிப்பாட்டிற்கு மாற்றுவோம். நாம் பெறுவது: 3 - 2 + C \u003d 0, எனவே C \u003d -1.

மொத்தம்: விரும்பிய சமன்பாடு: 3x - y - 1 = 0.

4. இரண்டு புள்ளிகள் வழியாக செல்லும் நேர்கோட்டின் சமன்பாடு

இரண்டு புள்ளிகள் M1 (x1 , y1 , z1 ) மற்றும் M2 (x2, y2 , z2 ) ஆகியவற்றை விண்வெளியில் கொடுக்கலாம், பின்னர் ஒரு நேர்கோட்டின் சமன்பாடு,

இந்த புள்ளிகள் வழியாக செல்கிறது:	x - x1				y - y1				z−z1
			− x				− ஒய்				− z

எந்தப் பிரிவும் பூஜ்ஜியத்திற்குச் சமமாக இருந்தால், அதனுடன் தொடர்புடைய எண் பூஜ்ஜியத்திற்குச் சமமாக அமைக்கப்பட வேண்டும்.

விமானத்தில், மேலே எழுதப்பட்ட நேர்கோட்டு சமன்பாடு எளிமைப்படுத்தப்பட்டுள்ளது: y - y 1 = y 2 - y 1 (x - x 1 ) என்றால் x 2 - x 1

x 1 ≠ x 2 மற்றும் x = x 1 என்றால் x 1 = x 2.

பின்னம் y 2 - y 1 = k நேர்கோட்டின் சாய்வு என்று அழைக்கப்படுகிறது. x2 - x1

5. ஒரு புள்ளி மற்றும் சாய்வின் அடிப்படையில் ஒரு நேர்கோட்டின் சமன்பாடு

Ax + By + C = 0 என்ற நேர் கோட்டின் பொதுவான சமன்பாடு படிவத்திற்கு இட்டுச் சென்றால்:

சாய்வு k உடன் நேர்கோட்டின் சமன்பாடு என்று அழைக்கப்படுகிறது.

6. ஒரு புள்ளி மற்றும் திசை திசையன் மூலம் ஒரு நேர் கோட்டின் சமன்பாடு

சாதாரண திசையன் வழியாக ஒரு நேர் கோட்டின் சமன்பாட்டைக் கருத்தில் கொண்டு புள்ளியுடன் ஒப்புமை மூலம், நீங்கள் ஒரு நேர் கோட்டின் மூலம் ஒரு நேர் கோட்டின் ஒதுக்கீட்டையும் ஒரு நேர் கோட்டின் திசையன் வழியாகவும் உள்ளிடலாம்.

வரையறை. ஒவ்வொரு பூஜ்ஜியமற்ற திசையன் a (α 1 ,α 2 ) அதன் கூறுகள் A α 1 + B α 2 = 0 நிபந்தனையை பூர்த்தி செய்யும் வரியின் திசையன் என்று அழைக்கப்படுகிறது

Ax + By + C = 0 .

உதாரணமாக. திசை திசையன் a (1,-1) மற்றும் புள்ளி A (1,2) வழியாக செல்லும் நேர்கோட்டின் சமன்பாட்டைக் கண்டறியவும்.

நாம் விரும்பிய நேர்க்கோட்டின் சமன்பாட்டை வடிவத்தில் தேடுவோம்: Ax + By + C = 0 . வரையறையின்படி, குணகங்கள் நிபந்தனைகளை பூர்த்தி செய்ய வேண்டும்: 1A + (− 1) B = 0 , அதாவது. A=B. பின்னர் நேர்கோட்டு சமன்பாடு இப்படி இருக்கும்: Ax + Ay + C = 0 , அல்லது x + y + C / A = 0 . x=1, y=2 இல் நாம் C/A=-3 ஐப் பெறுகிறோம், அதாவது. விரும்பிய சமன்பாடு: x + y - 3 = 0

7. பிரிவுகளில் நேர்கோட்டின் சமன்பாடு

Ax + By + C \u003d 0, C ≠ 0 என்ற வரியின் பொதுவான சமன்பாட்டில் இருந்தால், -С ஆல் வகுத்தால்,

நாம் பெறுகிறோம்: -

x-

y = 1 அல்லது

1, அங்கு a = -

b = -

குணகங்களின் வடிவியல் பொருள் என்னவென்றால், குணகம் a என்பது ஆக்ஸ் அச்சுடன் கோடு வெட்டும் புள்ளியின் ஒருங்கிணைப்பு ஆகும், மேலும் b என்பது Oy அச்சுடன் கோடு வெட்டும் புள்ளியின் ஒருங்கிணைப்பு ஆகும்.

8. ஒரு நேர்கோட்டின் இயல்பான சமன்பாடு

இயல்பாக்கும் காரணி என்று அழைக்கப்படுகிறது, பின்னர் நாம் x cosϕ + y sinϕ - p = 0, கோட்டின் இயல்பான சமன்பாட்டைப் பெறுகிறோம்.

இயல்பாக்கும் காரணியின் அடையாளம் ± தேர்ந்தெடுக்கப்பட வேண்டும், அதனால் μC< 0 .

p என்பது தோற்றத்திலிருந்து நேர் கோட்டிற்குக் குறைக்கப்பட்ட செங்குத்து நீளம், மேலும் ϕ என்பது எருது அச்சின் நேர் திசையுடன் இந்த செங்குத்தாக உருவான கோணமாகும்.

9. ஒரு விமானத்தில் கோடுகளுக்கு இடையே உள்ள கோணம்

வரையறை. இரண்டு கோடுகள் y \u003d k 1 x + b 1, y \u003d k 2 x + b 2 என வழங்கப்பட்டால், இடையே உள்ள தீவிர கோணம்

k 1 = k 2 எனில் இரண்டு கோடுகள் இணையாக இருக்கும். k 1 = - 1/ k 2 எனில் இரண்டு கோடுகள் செங்குத்தாக இருக்கும்.

கொடுக்கப்பட்ட கோட்டிற்கு செங்குத்தாக கொடுக்கப்பட்ட புள்ளியின் வழியாக செல்லும் கோட்டின் சமன்பாடு

வரையறை. புள்ளி M1 (x1, y1) மற்றும் y \u003d kx + b என்ற நேர் கோட்டிற்கு செங்குத்தாக செல்லும் நேர்கோடு சமன்பாட்டால் குறிக்கப்படுகிறது:

y - y = -

(x - x)

10. புள்ளியிலிருந்து வரிக்கு தூரம்

ஒரு புள்ளி M(x0, y0) கொடுக்கப்பட்டால், Ax + By + C = 0 என்ற வரிக்கான தூரம்

d = என வரையறுக்கப்படுகிறது

Ax0 + By0 + C

உதாரணமாக. கோடுகளுக்கு இடையே உள்ள கோணத்தை தீர்மானிக்கவும்: y = - 3x + 7, y = 2x + 1.

k = - 3, k

2டிஜி ϕ =

2 − (− 3)

1;ϕ = π / 4.

1− (− 3)2

உதாரணமாக. காட்டு,

கோடுகள் 3 x - 5 y + 7 = 0 மற்றும் 10 x + 6 y - 3 = 0

செங்குத்தாக உள்ளன.

நாம் காண்கிறோம்: k 1 \u003d 3/ 5, k 2 \u003d - 5 / 3, k 1 k 2 \u003d - 1, எனவே, கோடுகள் செங்குத்தாக உள்ளன.

உதாரணமாக. A(0 ; 1) , B (6 ; 5) , C (1 2 ; - 1) முக்கோணத்தின் செங்குத்துகள் கொடுக்கப்பட்டுள்ளன.

சியின் உச்சியிலிருந்து வரையப்பட்ட உயரத்திற்கான சமன்பாட்டைக் கண்டறியவும்.
AB பக்கத்தின் சமன்பாட்டைக் காண்கிறோம்:	x - 0		y - 1					y - 1		; 4x = 6y - 6
	6 − 0		5 − 1

2x - 3y + 3 = 0; y = 2 3 x + 1.

விரும்பிய உயரச் சமன்பாடு வடிவம் கொண்டது: Ax + By + C = 0 அல்லது y = kx + bk = - 3 2 பின்னர்

y = - 3 2 x + b . ஏனெனில் உயரம் புள்ளி C வழியாக செல்கிறது, அதன் ஒருங்கிணைப்புகள் இந்த சமன்பாட்டை பூர்த்தி செய்கின்றன: − 1 = - 3 2 12 + b , எங்கிருந்து b=17. மொத்தம்: y = - 3 2 x + 17 .

பதில்: 3x + 2y - 34 = 0 .

இலக்கு:ஒரு விமானத்தில் ஒரு கோட்டின் கருத்தைக் கவனியுங்கள், எடுத்துக்காட்டுகளைக் கொடுங்கள். ஒரு கோட்டின் வரையறையின் அடிப்படையில், ஒரு விமானத்தில் ஒரு நேர் கோட்டின் சமன்பாட்டின் கருத்தை அறிமுகப்படுத்துங்கள். ஒரு நேர் கோட்டின் வகைகளைக் கருத்தில் கொண்டு, ஒரு நேர் கோட்டை அமைப்பதற்கான எடுத்துக்காட்டுகளையும் வழிகளையும் கொடுங்கள். ஒரு நேர்கோட்டின் சமன்பாட்டை ஒரு பொது வடிவத்திலிருந்து ஒரு நேர்கோட்டின் சமன்பாட்டிற்கு "பிரிவுகளில்", ஒரு சாய்வுடன் மொழிபெயர்க்கும் திறனை ஒருங்கிணைக்க.

1. ஒரு விமானத்தில் ஒரு கோட்டின் சமன்பாடு.
2. ஒரு விமானத்தில் ஒரு நேர் கோட்டின் சமன்பாடு. சமன்பாடுகளின் வகைகள்.
3. நேர்கோட்டை அமைப்பதற்கான வழிகள்.

1. x மற்றும் y இரண்டு தன்னிச்சையான மாறிகளாக இருக்கட்டும்.

வரையறை: F(x,y)=0 வடிவத்தின் தொடர்பு அழைக்கப்படுகிறது சமன்பாடு , x மற்றும் y ஆகிய எந்த ஜோடி எண்களுக்கும் இது செல்லுபடியாகவில்லை என்றால்.

உதாரணமாக: 2x + 7y - 1 \u003d 0, x 2 + y 2 - 25 \u003d 0.

சமத்துவம் F(x,y)=0 எந்த x, y க்கும் இருந்தால், அதன் விளைவாக, F(x,y) = 0 என்பது ஒரு அடையாளமாகும்.

எடுத்துக்காட்டு: (x + y) 2 - x 2 - 2xy - y 2 = 0

x என்பது 0 என்றும் y என்பது 0 என்றும் சொல்கிறார்கள் சமன்பாட்டை திருப்திப்படுத்தவும் , இந்த சமன்பாட்டில் அவை மாற்றப்படும் போது, ​​அது உண்மையான சமத்துவமாக மாறும்.

பகுப்பாய்வு வடிவவியலின் மிக முக்கியமான கருத்து ஒரு கோட்டின் சமன்பாட்டின் கருத்து.

வரையறை: கொடுக்கப்பட்ட கோட்டின் சமன்பாடு F(x,y)=0 சமன்பாடு ஆகும், இது இந்த வரியில் இருக்கும் அனைத்து புள்ளிகளின் ஆயத்தொலைவுகளாலும் திருப்திப்படுத்தப்படுகிறது, மேலும் இந்த வரியில் இல்லாத எந்த புள்ளிகளின் ஆயத்தொலைவுகளாலும் திருப்தி அடையாது.

y = f(x) சமன்பாட்டால் வரையறுக்கப்பட்ட கோடு f(x) செயல்பாட்டின் வரைபடம் எனப்படும். மாறிகள் x மற்றும் y ஆகியவை தற்போதைய ஆயத்தொலைவுகள் என்று அழைக்கப்படுகின்றன, ஏனெனில் அவை மாறி புள்ளியின் ஆயத்தொலைவுகள்.

சில உதாரணங்கள்வரி வரையறைகள்.

1) x - y \u003d 0 \u003d\u003e x \u003d y. இந்த சமன்பாடு ஒரு நேர் கோட்டை வரையறுக்கிறது:

2) x 2 - y 2 \u003d 0 => (x-y) (x + y) \u003d 0 => புள்ளிகள் x - y \u003d 0 சமன்பாட்டை அல்லது x + y \u003d 0 சமன்பாட்டை பூர்த்தி செய்ய வேண்டும். ஒரு ஜோடி வெட்டும் கோடுகளுக்கு, அவை ஆயக் கோணங்களின் இரு பிரிவுகளாகும்:

3) x 2 + y 2 \u003d 0. ஒரே ஒரு புள்ளி O (0,0) மட்டுமே இந்த சமன்பாட்டை பூர்த்தி செய்கிறது.

2. வரையறை: விமானத்தில் உள்ள எந்த வரியையும் முதல் வரிசை சமன்பாட்டின் மூலம் கொடுக்கலாம்

ஆ + வு + சி = 0,

மேலும், மாறிலிகள் A, B ஒரே நேரத்தில் பூஜ்ஜியத்திற்கு சமமாக இல்லை, அதாவது. A 2 + B 2 ¹ 0. இந்த முதல்-வரிசை சமன்பாடு அழைக்கப்படுகிறது ஒரு நேர் கோட்டின் பொதுவான சமன்பாடு.

A, B மற்றும் C மாறிலிகளின் மதிப்புகளைப் பொறுத்து, பின்வரும் சிறப்பு நிகழ்வுகள் சாத்தியமாகும்:

C \u003d 0, A ¹ 0, B ¹ 0 - கோடு தோற்றம் வழியாக செல்கிறது

A \u003d 0, B ¹ 0, C ¹ 0 ( By + C \u003d 0) - கோடு ஆக்ஸ் அச்சுக்கு இணையாக உள்ளது

B \u003d 0, A ¹ 0, C ¹ 0 (Ax + C \u003d 0) - கோடு Oy அச்சுக்கு இணையாக உள்ளது

B \u003d C \u003d 0, A ¹ 0 - நேர் கோடு Oy அச்சுடன் ஒத்துப்போகிறது

A \u003d C \u003d 0, B ¹ 0 - நேர் கோடு ஆக்ஸ் அச்சுடன் ஒத்துப்போகிறது

ஒரு நேர்கோட்டின் சமன்பாடு கொடுக்கப்பட்ட ஆரம்ப நிலைகளைப் பொறுத்து பல்வேறு வடிவங்களில் குறிப்பிடப்படலாம்.

ஒரு சாய்வு கொண்ட ஒரு நேர் கோட்டின் சமன்பாடு.

Ax + Vy + C = 0 என்ற நேர் கோட்டின் பொதுவான சமன்பாடு படிவத்திற்கு இட்டுச் சென்றால்:

மற்றும் குறிக்கவும், அதன் விளைவாக சமன்பாடு அழைக்கப்படுகிறது சாய்வு k உடன் நேர்கோட்டின் சமன்பாடு.

பிரிவுகளில் நேர்கோட்டின் சமன்பாடு.

Ax + Vy + С = 0 С ¹ 0 என்ற நேர்கோட்டின் பொதுவான சமன்பாட்டில் இருந்தால், –С ஆல் வகுத்தால், நமக்கு கிடைக்கும்: அல்லது , எங்கே

குணகங்களின் வடிவியல் பொருள் குணகம் ஏ x அச்சுடன் கோட்டின் வெட்டும் புள்ளியின் ஒருங்கிணைப்பு ஆகும், மற்றும் பி- Oy அச்சுடன் நேர் கோட்டின் வெட்டும் புள்ளியின் ஒருங்கிணைப்பு.

ஒரு நேர்கோட்டின் இயல்பான சமன்பாடு.

Ax + Wy + C = 0 என்ற சமன்பாட்டின் இரு பக்கமும் ஒரு எண்ணால் வகுத்தால் இயல்பாக்கும் காரணி, பிறகு நாம் பெறுவோம்

xcosj + ysinj - p = 0 என்பது ஒரு நேர்கோட்டின் இயல்பான சமன்பாடு.

இயல்பாக்கும் காரணியின் அடையாளம் ± தேர்ந்தெடுக்கப்பட வேண்டும், அதனால் m × С< 0.

p என்பது தோற்றத்திலிருந்து நேர் கோட்டிற்குக் குறைக்கப்பட்ட செங்குத்து நீளம், மற்றும் j என்பது ஆக்ஸ் அச்சின் நேர்மறை திசையுடன் இந்த செங்குத்தாக உருவாகும் கோணம்.

3. ஒரு புள்ளி மற்றும் சாய்வு மூலம் நேர்கோட்டின் சமன்பாடு.

நேர்கோட்டின் சாய்வு k க்கு சமமாக இருக்கட்டும், நேர்கோடு புள்ளி M(x 0, y 0) வழியாக செல்கிறது. பின்னர் நேர் கோட்டின் சமன்பாடு சூத்திரத்தால் கண்டறியப்படுகிறது: y - y 0 \u003d k (x - x 0)

இரண்டு புள்ளிகள் வழியாக செல்லும் நேர்கோட்டின் சமன்பாடு.

இரண்டு புள்ளிகள் M 1 (x 1, y 1, z 1) மற்றும் M 2 (x 2, y 2, z 2) ஆகியவற்றை விண்வெளியில் கொடுக்கலாம், பின்னர் இந்த புள்ளிகள் வழியாக செல்லும் நேர்கோட்டின் சமன்பாடு:

எந்தப் பிரிவும் பூஜ்ஜியத்திற்குச் சமமாக இருந்தால், அதனுடன் தொடர்புடைய எண் பூஜ்ஜியத்திற்குச் சமமாக அமைக்கப்பட வேண்டும்.

ஒரு விமானத்தில், மேலே எழுதப்பட்ட ஒரு நேர்கோட்டின் சமன்பாடு எளிமைப்படுத்தப்பட்டுள்ளது:

x 1 ¹ x 2 மற்றும் x \u003d x 1 என்றால், x 1 \u003d x 2.

பின்னம் = k என்று அழைக்கப்படுகிறது சாய்வு காரணிநேராக.

டெபாசிட் கோப்புகளிலிருந்து பதிவிறக்கவும்

பகுப்பாய்வு வடிவியல்

விரிவுரை எண் 7. தலைப்பு 1 : விமானத்தில் உள்ள கோடுகள் மற்றும் அவற்றின் சமன்பாடுகள்

1.1 கார்ட்டீசியன் ஆயங்களில் கோடுகள் மற்றும் அவற்றின் சமன்பாடுகள்

பகுப்பாய்வு வடிவவியலில், ஒரு விமானத்தில் உள்ள கோடுகள், கோட்டின் அனைத்துப் புள்ளிகளுக்கும் பொதுவான ஒரே பண்புகளைக் கொண்ட புள்ளிகளின் இருப்பிடமாக (g.m.t.) கருதப்படுகிறது.

வரையறை. வரி சமன்பாடு
இரண்டு மாறிகள் கொண்ட ஒரு சமன்பாடுஎக்ஸ்மற்றும் மணிக்கு, இது வரியில் உள்ள எந்தப் புள்ளியின் ஆயத்தொலைவுகளாலும் திருப்தி அடையும் மற்றும் இந்தக் கோட்டில் அமையாத வேறு எந்தப் புள்ளியின் ஆயத்தொலைவுகளாலும் திருப்தி அடையாது.

உரையாடலும் உண்மை, அதாவது. எந்த சமன்பாடுமணிக்கு

கார்டீசியனில் பொதுவாகப் பேசும் படிவத்தின்

ஒருங்கிணைப்பு அமைப்பு (DSC) ஒரு வரியை வரையறுக்கிறது

ஒரு g.m.t. ஆக, அதன் ஒருங்கிணைப்புகள் திருப்தி அளிக்கின்றன

இந்த சமன்பாடு.பற்றி எக்ஸ்

குறிப்பு 1. ஒவ்வொரு வகை சமன்பாடும் ஒரு கோட்டை வரையறுப்பதில்லை. உதாரணமாக, சமன்பாட்டிற்கு
இந்த சமன்பாட்டை திருப்திப்படுத்தும் புள்ளிகள், ஆயத்தொலைவுகள் எதுவும் இல்லை. அத்தகைய வழக்குகள் மேலும் பரிசீலிக்கப்படாது.கற்பனைக் கோடுகள் என்று சொல்லப்படுவது இதுதான்.

பி உதாரணம் 1.ஆரம் கொண்ட ஒரு வட்டத்திற்கு ஒரு சமன்பாட்டை எழுதுங்கள்ஆர் ஒரு புள்ளியை மையமாகக் கொண்டது
.

எந்த விஷயத்திற்கும் பொய்மணிக்குஎம்

ஒரு வட்டத்தில், வரையறையின்படிஆர்

வட்டங்கள் g.m.t., சம தூரம்

புள்ளியில் இருந்து, நாம் சமன்பாட்டைப் பெறுகிறோம்எக்ஸ்

1.2 கோடுகளின் அளவுரு சமன்பாடுகள்

எனப்படும் சமன்பாடுகளைப் பயன்படுத்தி ஒரு விமானத்தில் ஒரு கோட்டை வரையறுக்க மற்றொரு வழி உள்ளதுஅளவுரு:

உதாரணம் 1 கோடு அளவுரு சமன்பாடுகளால் வழங்கப்படுகிறது

டிஎஸ்சியில் இந்த வரியின் சமன்பாட்டைப் பெறுவது அவசியம்.

அளவுருவை விலக்குடி . இதைச் செய்ய, இந்த சமன்பாடுகளின் இருபுறமும் சதுரம் மற்றும் சேர்க்கிறோம்

எடுத்துக்காட்டு 2 கோடு அளவுரு சமன்பாடுகளால் வழங்கப்படுகிறது

ஏ

சமன்பாட்டைப் பெற இது தேவைப்படுகிறது

டிஎஸ்சியில் இந்த வரி. —ஒரு அ

அதையே செய்வோம், பிறகு கிடைக்கும்

— ஏ

குறிப்பு 2. அளவுரு என்பதை கவனத்தில் கொள்ள வேண்டும்டி இயக்கவியலில் நேரம்.

1.3 துருவ ஆயங்களில் கோடு சமன்பாடு

DSC என்பது ஒரு புள்ளியின் நிலையை தீர்மானிக்க ஒரே வழி அல்ல, எனவே ஒரு கோட்டின் சமன்பாடு. ஒரு விமானத்தில், துருவ ஒருங்கிணைப்பு அமைப்பு (PSC) என்று அழைக்கப்படுவதைப் பயன்படுத்துவது பெரும்பாலும் பொருத்தமானது.

பி ஒரு புள்ளியைக் குறிப்பிடுவதன் மூலம் SC தீர்மானிக்கப்படும்ஓ - கம்பம் மற்றும் பீம் அல்லது இந்த புள்ளியிலிருந்து வெளிப்படுகிறது, இது துருவ அச்சு என்று அழைக்கப்படுகிறது. எந்த புள்ளியின் நிலையும் இரண்டு எண்களால் தீர்மானிக்கப்படுகிறது: துருவ ஆரம்
மற்றும் துருவ கோணம் இடையே உள்ள கோணம்

துருவ அச்சு மற்றும் துருவ ஆரம்.

நேர்மறை குறிப்பு திசை

துருவ அச்சில் இருந்து துருவ கோணம்

எதிரெதிர் திசையில் எண்ணப்பட்டது.

விமானத்தின் அனைத்து புள்ளிகளுக்கும்
, அல்லது

மற்றும் துருவ கோணத்தின் தனித்தன்மைக்காக இது கருதப்படுகிறது
.

டிஎஸ்சியின் ஆரம்பம் இணைந்தால்

துருவம் மற்றும் O அச்சு எக்ஸ்மூலம் அனுப்பு

துருவ அச்சு, சரிபார்க்க எளிதானதுமணிக்கு

துருவ மற்றும் இடையே தொடர்பில்

கார்ட்டீசியன் ஆயத்தொகுப்புகள்:

பற்றி எக்ஸ்ஆர்

மீண்டும்,

(1)

டிஎஸ்சியில் உள்ள கோட்டுச் சமன்பாட்டில் படிவம் இருந்தால், பிஎஸ்சியில் - இந்த சமன்பாட்டிலிருந்து படிவத்தில் ஒரு சமன்பாட்டைப் பெறலாம்.

எடுத்துக்காட்டு 3 வட்டத்தின் மையம் துருவத்தில் இருந்தால், UCS இல் வட்டத்தின் சமன்பாட்டை எழுதவும்.

DSC இலிருந்து PSC க்கு மாறுதல் சூத்திரங்களைப் (1) பயன்படுத்தி, நாங்கள் பெறுகிறோம்

பி உதாரணம் 4.ஒரு வட்டத்திற்கு ஒரு சமன்பாட்டை எழுதுங்கள்

துருவமானது வட்டம் மற்றும் துருவ அச்சில் இருந்தால்மணிக்கு

விட்டம் வழியாக செல்கிறது.

அதையே செய்வோம்

சுமார் 2 ஆர் எக்ஸ்

ஆர்

இந்த சமன்பாட்டையும் பெறலாம்

வடிவியல் பிரதிநிதித்துவங்களிலிருந்து (அத்தி பார்க்கவும்).

பி உதாரணம் 5.ப்ளாட் லைன்

PSC க்கு செல்லலாம். சமன்பாடு

வடிவம் எடுக்கும்
பற்றி

நாங்கள் வரியை திட்டமிடுவோம்ஏ

அதன் சமச்சீர் மற்றும் ODZ கணக்கில் எடுத்துக்கொள்வது

அம்சங்கள்:

இந்த வரி அழைக்கப்படுகிறதுலெம்னிஸ்கேட் பெர்னோலி.

1.4 ஒருங்கிணைப்பு அமைப்பு மாற்றம்.

புதிய ஒருங்கிணைப்பு அமைப்பில் கோடு சமன்பாடு

1. DSC இன் இணையான பரிமாற்றம்.மணிக்கு

இரண்டு டிஎஸ்சிகளைக் கவனியுங்கள்எம்

அச்சுகளின் அதே திசையில், ஆனால்

வெவ்வேறு தோற்றம்.

ஒருங்கிணைப்பு அமைப்பில்பற்றி ஹூபுள்ளி

அமைப்பு தொடர்பாக
பற்றி எக்ஸ்

ஆய உள்ளது
. பின்னர் நாம்

மற்றும்

ஒருங்கிணைப்பு வடிவத்தில், இதன் விளைவாக வரும் திசையன் சமத்துவம் வடிவம் கொண்டது

அல்லது
. (2)

சூத்திரங்கள் (2) என்பது "பழைய" ஒருங்கிணைப்பு அமைப்பிலிருந்து மாறுவதற்கான சூத்திரங்கள்பற்றி ஹூ"புதிய" ஒருங்கிணைப்பு அமைப்புக்கு மற்றும் நேர்மாறாகவும்.

உதாரணம் 5 ஒருங்கிணைப்பு அமைப்பின் இணையான மொழிபெயர்ப்பைச் செய்வதன் மூலம் ஒரு வட்டத்தின் சமன்பாட்டைப் பெறவும்வட்டத்தின் மையத்திற்கு.

மற்றும் 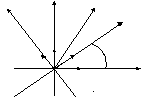சூத்திரங்களிலிருந்து (2) அது பின்வருமாறு
மணிக்கு ONPost வழிசெலுத்தல்