Hľadá sa opak. Nájdite inverznú maticu online. Algebraické doplnky a maloletí

1. Nájdite determinant pôvodnej matice. Ak je potom matica zdegenerovaná a inverzná matica neexistuje. Ak, potom je matica nedegenerovaná a existuje inverzná matica.

2. Nájdite maticu transponovanú do.

3. Nájdite algebraické doplnky prvkov a zostavte z nich adjungovanú maticu.

4. Inverznú maticu skladáme podľa vzorca.

5. Skontrolujte správnosť výpočtu inverznej matice na základe jej definície:.

Príklad.Nájdite inverznú hodnotu danej matice :.

Rozhodnutie.

1) Maticový determinant

.

2) Nájdite algebraické doplnky prvkov matice a z nich zostavte adjunkčnú maticu:

3) Vypočítajte inverznú maticu:

,

4) Skontrolujte:

№4 Poradie matice. Lineárna nezávislosť riadkov matice

Pre riešenie a výskum mnohých matematických a aplikovaných problémov je veľmi dôležitý koncept hodnosti matice.

V matici veľkosti môžete vyčiarknutím niektorých riadkov a stĺpcov izolovať štvorcové podmatrice toho rádu, kde. Determinanty takýchto submatíc sa volajú maloletí desiateho rádu matice .

Napríklad matice možno použiť na získanie submatíc 1., 2. a 3. rádu.

Definícia. Poradie matice je najvyšší rad nenulových maloletých tejto matice. Označenie: alebo.

Z definície vyplýva:

1) Poradie matice nepresahuje menšie z jej rozmerov, t.j.

2) práve vtedy, ak sú všetky prvky matice rovné nule, t.j.

3) Pre štvorcovú maticu rádu n práve vtedy, ak je nedegenerovaná.

Pretože priamy výpočet všetkých možných maloletých matice, počnúc najväčšou veľkosťou, je zložitý (časovo náročný), potom použijeme transformácie elementárnych matíc, ktoré zachovajú hodnosť matice.

Transformácie základnej matice:

1) Zrušenie nulového riadku (stĺpca).

2) Násobenie všetkých prvkov riadku (stĺpca) číslom.

3) Zmena poradia riadkov (stĺpcov) matice.

4) Ku každému prvku jedného riadku (stĺpca) sa pripočítajú príslušné prvky iného riadku (stĺpca) vynásobené ľubovoľným číslom.

5) Transponujte maticu.

Definícia. Matica získaná z matice pomocou elementárnych transformácií sa nazýva ekvivalentná a označuje sa A IN.

Veta. Poradie matice sa pri transformáciách elementárnej matice nemení.

Pomocou elementárnych transformácií je možné maticu zmenšiť na takzvanú stupňovitú formu, keď výpočet jej poradia nie je zložitý.

Matica sa volá postupne, ak má tvar:

Je zrejmé, že poradie stupňovitej matice sa rovná počtu nenulových riadkov existuje menšia objednávka, ktorá sa nerovná nule:

.

Príklad. Určte poradie matice pomocou elementárnych transformácií.

Poradie matice sa rovná počtu nenulových riadkov, t.j. ...

№5Lineárna nezávislosť riadkov matice

Daná matica veľkosti

Označme riadky matice takto:

Tieto dva riadky sa nazývajú rovný ak sú ich zodpovedajúce prvky rovnaké. ...

Predstavíme si operácie vynásobenia reťazca číslom a pridania reťazcov ako operácií vykonávaných prvok po prvku:

Definícia. Reťazec sa nazýva lineárna kombinácia riadkov matice, ak sa rovná súčtu súčinov týchto reťazcov ľubovoľnými reálnymi číslami (ľubovoľnými číslami):

Definícia. Matičné riadky sa volajú lineárne závislé ak existujú také čísla, ktoré nie sú súčasne nulové, takže lineárna kombinácia riadkov matice sa rovná nulovému riadku:

Kde. (1.1)

Lineárna závislosť riadkov matice znamená, že najmenej 1 riadok matice je lineárnou kombináciou zvyšku.

Definícia. Ak je lineárna kombinácia riadkov (1.1) nulová práve vtedy, ak sú všetky koeficienty, potom sa riadok zavolá lineárne nezávislé .

Maticová veta o hodnosti . Poradie matice sa rovná maximálnemu počtu jej lineárne nezávislých riadkov alebo stĺpcov, cez ktoré sú lineárne vyjadrené všetky ostatné riadky (stĺpce).

Veta hrá zásadnú úlohu v maticovej analýze, najmä pri štúdiu systémov lineárnych rovníc.

№6 Riešenie sústavy lineárnych rovníc s neznámymi

Systémy lineárnych rovníc sú široko používané v ekonómii.

Sústava lineárnych rovníc s premennými má tvar:

,

kde () sa volajú ľubovoľné čísla koeficienty pre premenné a voľné termíny rovníc , resp.

Krátky vstup: ().

Definícia. Riešením systému je množina hodnôt, ktorá po nahradení zmení každú rovnicu v systéme na skutočnú rovnosť.

1) Systém rovníc sa volá kĺb - ak má aspoň jedno riešenie, a - nedôslednéak nemá riešenie.

2) Spoločná sústava rovníc sa nazýva istý - ak má jedinečné riešenie, a - nedefinované ak má viac ako jedno riešenie.

3) Zavolajú sa dva systémy rovníc ekvivalent (ekvivalent ) ak majú rovnakú sadu riešení (napríklad jedno riešenie).

Inverzná matica pre danú z nich je taká matica, ktorá vynásobí pôvodnú hodnotu a dá maticu identity: Povinnou a dostatočnou podmienkou pre prítomnosť inverznej matice je nerovnosť pôvodného determinantu na nulu (z čoho vyplýva, že matica musí byť štvorcová). Ak sa determinant matice rovná nule, potom sa nazýva zdegenerovaná a takáto matica nemá inverznú hodnotu. Vo vyššej matematike sú inverzné matice dôležité a používajú sa na riešenie množstva problémov. Napríklad na nájdenie inverznej matice je skonštruovaná maticová metóda na riešenie sústav rovníc. Naše stránky služieb to umožňujú vypočítať inverznú maticu online dve metódy: Gauss-Jordanova metóda a použitie matice algebraických doplnkov. Prvá implikuje veľké množstvo elementárnych transformácií vo vnútri matice, druhá - výpočet determinantu a algebraických doplnkov ku všetkým prvkom. Ak chcete vypočítať determinant matice online, môžete použiť našu ďalšiu službu - Vypočítajte determinant matice online

Nájdite inverznú maticu webu

webovú stránku umožňuje nájsť inverzná matica online rýchlo a zadarmo. Na stránke vykonáva výpočty naša služba a je vydaný výsledok s podrobným riešením na nájdenie inverzná matica... Server vždy dáva iba presnú a správnu odpoveď. V úlohách podľa definície inverzná matica online, je potrebné, aby determinant matice bol nenulový, inak webovú stránku bude hlásiť nemožnosť nájdenia inverznej matice z dôvodu rovnosti determinantu pôvodnej matice na nulu. Úloha nájsť inverzná matica nájdený v mnohých odvetviach matematiky, ktorý je jedným z najzákladnejších pojmov algebry a matematickým nástrojom v aplikovaných problémoch. Nezávislý definícia inverznej matice vyžaduje veľa úsilia, veľa času, výpočtov a veľkú opatrnosť, aby sa zabránilo skĺznutiu alebo menšej chybe vo výpočtoch. Preto je naša služba pre nájdenie inverznej matice online výrazne uľahčí vašu úlohu a stane sa nepostrádateľným nástrojom na riešenie matematických úloh. Aj keď ty nájdi inverznú hodnotu matice sami, odporúčame skontrolovať vaše riešenie na našom serveri. Zadajte svoju pôvodnú maticu na našom výpočte inverznej matice online a skontrolujte svoju odpoveď. Náš systém nikdy nezlyhá a nájde inverzná matica daný rozmer v režime online okamžite! Na strane webovú stránku zadávanie znakov je povolené v prvkoch matice, v tomto prípade inverzná matica online budú predstavené vo všeobecnej symbolickej podobe.

ALGEBRAICKÉ DOPLNKY A DOSPELÉ

Poďme mať determinant tretieho rádu: .

Menšiezodpovedajúce tomuto prvku a ij determinant tretieho rádu, sa nazýva determinant druhého rádu, získaný z daného odstránením riadku a stĺpca, na ktorých priesečníku daný prvok stojí, t.j. i-ty riadok a jth stĺpec. Neplnoleté osoby zodpovedajúce danému prvku a ij bude naznačovať M ij.

napríklad, maloletý M 12zodpovedajúci prvku a 12, bude existovať determinant 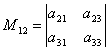, ktorá sa získa vymazaním 1. riadku a 2. stĺpca z daného determinantu.

Vzorec definujúci determinant tretieho rádu teda ukazuje, že tento determinant sa rovná súčtu súčinov prvkov 1. riadku zodpovedajúcimi maloletými; minor zodpovedajúci prvku a 12, odobraté znakom „-“, t.j. to môžeme napísať

Podobne môžeme zaviesť definície maloletých pre determinanty druhého rádu a vyšších rádov.

Poďme predstaviť ešte jeden koncept.

Algebraický doplnokprvok a ij determinant sa nazýva jeho vedľajší M ijvynásobené (–1) i + j.

Algebraický doplnok prvku a ij označené A ij.

Z definície získame, že spojenie medzi algebraickým doplnkom prvku a jeho vedľajším je vyjadrené rovnosťou A ij \u003d (–1) i + j M ij.

Napríklad,

Príklad. Uvádza sa determinant. Nájsť A 13, A 21, A 32.

Je ľahké vidieť, že pomocou algebraických doplnkov prvkov možno vzorec (1) zapísať vo forme:

Podobne ako v tomto vzorci môžete získať rozklad determinantu na prvky ľubovoľného riadku alebo stĺpca.

Napríklad faktorizáciu determinantu prvkami 2. riadku je možné získať nasledovne. Podľa vlastnosti 2 determinantu máme:

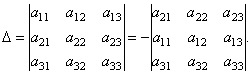
Rozširujme výsledný determinant o prvky 1. riadku.

.

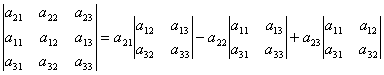(2)

Odtiaľ odkedy determinanty druhého rádu vo vzorci (2) sú neplnoleté prvky a 21, 22, 23... Teda t.j. dostali sme rozklad determinantu z hľadiska prvkov 2. radu.

Podobne môžete získať faktorizáciu determinantu prvkami tretieho radu. Použitím vlastnosti 1 determinantov (pri transpozícii) je možné ukázať, že podobné rozšírenia platia aj pre rozšírenie, pokiaľ ide o prvky stĺpcov.

Nasledujúca veta je teda pravdivá.

Veta (o rozšírení determinantu v danom riadku alebo stĺpci). Determinant sa rovná súčtu súčinov prvkov ktoréhokoľvek z jeho riadkov (alebo stĺpcov) pomocou ich algebraických doplnkov.

Všetko vyššie uvedené platí aj pre determinanty vyššieho rádu.

Príklady.

INVERZNÁ MATICA

Koncept inverznej matice je zavedený iba pre štvorcové matice.

Ak A Je teda štvorcová matica obrátiť pre to je matica matica označená A -1 a splnenie podmienky. (Táto definícia sa zavádza analogicky s násobením čísel)

V tomto článku si povieme niečo o maticovej metóde riešenia sústavy lineárnych algebraických rovníc, nájdeme jej definíciu a uvedieme príklady riešenia.

Definícia 1

Metóda inverznej matice je metóda používaná na riešenie SLAE v prípade, že počet neznámych sa rovná počtu rovníc.

Príklad 1

Nájdite riešenie pre systém n lineárnych rovníc s n neznámymi:

a 11 x 1 + a 12 x 2 +. ... ... + a 1 n x n \u003d b 1 a n 1 x 1 + a n 2 x 2 +. ... ... + a n n x n \u003d b n

Maticový záznam : A × X \u003d B

kde А \u003d а 11 а 12 ⋯ а 1 n а 21 а 22 ⋯ а 2 n ⋯ ⋯ ⋯ ⋯ а n 1 а n 2 ⋯ а n n - matica systému.

X \u003d x 1 x 2 ⋮ x n - stĺpec neznámych,

B \u003d b 1 b 2 ⋮ b n - stĺpec voľných koeficientov.

Z rovnice, ktorú sme dostali, je potrebné vyjadriť X. Aby ste to dosiahli, musíte vynásobiť obe strany maticovej rovnice vľavo znakom A - 1:

A - 1 × A × X \u003d A - 1 × B.

Pretože A - 1 × A \u003d E, potom E × X \u003d A - 1 × B alebo X \u003d A - 1 × B.

Komentovať

Inverzná matica k matici A má právo na existenciu, iba ak podmienka d e t A nie je rovná nule. Preto pri riešení SLAE metódou inverznej matice najskôr predovšetkým d e t A.

V prípade, že d e t A nie je rovné nule, má systém iba jedno riešenie: pomocou metódy inverznej matice. Ak d e t А \u003d 0, potom systém nemožno vyriešiť touto metódou.

Príklad riešenia sústavy lineárnych rovníc metódou inverznej matice

SLAE riešime metódou inverznej matice:

2 x 1 - 4 x 2 + 3 x 3 \u003d 1 x 1 - 2 x 2 + 4 x 3 \u003d 3 3 x 1 - x 2 + 5 x 3 \u003d 2

Ako riesit

• Systém píšeme vo forme maticovej rovnice A X \u003d B, kde

A \u003d 2 - 4 3 1 - 2 4 3 - 1 5, X \u003d x 1 x 2 x 3, B \u003d 1 3 2.

• Z tejto rovnice vyjadríme X:

• Nájdite determinant matice A:

det A \u003d 2 - 4 3 1 - 2 4 3 - 1 5 \u003d 2 × (- 2) × 5 + 3 × (- 4) × 4 + 3 × (- 1) × 1 - 3 × (- 2) × 3 - - 1 × (- 4) × 5 - 2 × 4 - (- 1) \u003d - 20 - 48 - 3 + 18 + 20 + 8 \u003d - 25

d e t А sa nerovná 0, preto je pre tento systém vhodná metóda riešenia inverznej matice.

• Vyhľadajte inverznú maticu A - 1 pomocou spojovacej matice. Vypočítame algebraické doplnky A i j k zodpovedajúcim prvkom matice A:

A 11 \u003d (- 1) (1 + 1) - 2 4 - 1 5 \u003d - 10 + 4 \u003d - 6,

A 12 \u003d (- 1) 1 + 2 1 4 3 5 \u003d - (5 - 12) \u003d 7,

A 13 \u003d (- 1) 1 + 3 1 - 2 3 - 1 \u003d - 1 + 6 \u003d 5,

A 21 \u003d (- 1) 2 + 1 - 4 3 - 1 5 \u003d - (- 20 + 3) \u003d 17,

A 22 \u003d (- 1) 2 + 2 2 3 3 5 - 10 - 9 \u003d 1,

A 23 \u003d (- 1) 2 + 3 2 - 4 3 - 1 \u003d - (- 2 + 12) \u003d - 10,

A 31 \u003d (- 1) 3 + 1 - 4 3 - 2 4 \u003d - 16 + 6 \u003d - 10,

A 32 \u003d (- 1) 3 + 2 2 3 1 4 \u003d - (8 - 3) \u003d - 5,

A 33 \u003d (- 1) 3 + 3 2 - 4 1 - 2 \u003d - 4 + 4 \u003d 0.

• Zapíšeme jednotnú maticu A *, ktorá sa skladá z algebraických doplnkov matice A:

A * \u003d - 6 7 5 17 1 - 10 - 10 - 5 0

• Inverznú maticu zapíšeme podľa vzorca:

A - 1 \u003d 1 d e t A (A *) T: A - 1 \u003d - 1 25 - 6 17 - 10 7 1 - 5 5 - 10 0,

• Vynásobíme inverznú maticu A - 1 stĺpcom voľných výrazov B a dostaneme riešenie do systému:

X \u003d A - 1 × B \u003d - 1 25 - 6 17 - 10 7 1 - 5 5 - 10 0 1 3 2 \u003d - 1 25 - 6 + 51 - 20 7 + 3 - 10 5 - 30 + 0 \u003d - 1 0 1

Odpoveď : x 1 \u003d - 1; x 2 \u003d 0; x 3 \u003d 1

Ak si všimnete chybu v texte, vyberte ju a stlačte Ctrl + Enter

Matica $ A ^ (- 1) $ sa nazýva inverzná vzhľadom na štvorcovú maticu $ A $, ak je splnená podmienka $ A ^ (- 1) \\ cdot A \u003d A \\ cdot A ^ (- 1) \u003d E $, kde $ E $ Je matica identity, ktorej poradie sa rovná poradiu matice $ A $.

Nedegenerovaná matica - matica, ktorej determinant sa nerovná nule. V súlade s tým je zdegenerovaná matica s determinantom rovným nule.

Inverzná matica $ A ^ (- 1) $ existuje práve vtedy, ak je matica $ A $ nedegenerovaná. Ak inverzná matica $ A ^ (- 1) $ existuje, je jedinečná.

Existuje niekoľko spôsobov, ako nájsť inverziu matice, a pozrieme sa na dva z nich. Táto stránka bude pojednávať o metóde adjoint matrix, ktorá sa považuje za štandardnú vo väčšine kurzov vyššej matematiky. Druhá metóda hľadania inverznej matice (metóda elementárnych transformácií), ktorá spočíva v použití metódy Gauss alebo Gauss-Jordan, je diskutovaná v druhej časti.

Metóda spojenej (spojovacej) matice

Nech je zadaná matica $ A_ (n \\ krát n) $. Na nájdenie inverznej hodnoty matice $ A ^ (- 1) $ sú potrebné tri kroky:

1. Nájdite determinant matice $ A $ a uistite sa, že $ \\ Delta A \\ neq 0 $, t.j. že matica A je nedegenerovaná.
2. Vytvorte algebraické doplnky $ A_ (ij) $ každého prvku matice $ A $ a z nájdených algebraických doplnkov napíšte maticu $ A_ (n \\ krát n) ^ (*) \u003d \\ left (A_ (ij) \\ right) $.
3. Napíšte inverznú maticu so zohľadnením vzorca $ A ^ (- 1) \u003d \\ frac (1) (\\ Delta A) \\ cdot (A ^ (*)) ^ T $.

Matica $ (A ^ (*)) ^ T $ sa často označuje ako adjunkt (vzájomný, adjoint) k matici $ A $.

Ak sa riešenie robí ručne, potom je prvý spôsob vhodný iba pre matice relatívne malých objednávok: second (), third (), quarter (). Na nájdenie inverznej hodnoty matice vyššieho rádu sa používajú iné metódy. Napríklad Gaussova metóda, ktorej sa venuje druhá časť.

Príklad č

Nájdite inverznú hodnotu $ A \u003d \\ left (\\ begin (array) (cccc) 5 & -4 & 1 & 0 \\\\ 12 & -11 & 4 & 0 \\\\ -5 & 58 & 4 & 0 \\\\ 3 & - 1 & -9 & 0 \\ end (pole) \\ vpravo) $.

Pretože všetky prvky štvrtého stĺpca sú rovné nule, potom $ \\ Delta A \u003d 0 $ (t.j. matica $ A $ je zdegenerovaná). Pretože $ \\ Delta A \u003d 0 $, inverzná matica k matici $ A $ neexistuje.

Odpoveď: matica $ A ^ (- 1) $ neexistuje.

Príklad č

Nájdite inverznú hodnotu matice $ A \u003d \\ left (\\ begin (array) (cc) -5 & 7 \\\\ 9 & 8 \\ end (array) \\ right) $. Skontrolujte.

Používame metódu adjoint matrix. Najskôr nájdeme determinant danej matice $ A $:

$$ \\ Delta A \u003d \\ vľavo | \\ begin (pole) (cc) -5 & 7 \\\\ 9 & 8 \\ end (pole) \\ vpravo | \u003d -5 \\ cdot 8-7 \\ cdot 9 \u003d -103. $$

Pretože $ \\ Delta A \\ neq 0 $, potom existuje inverzná matica, takže pokračujeme v riešení. Hľadanie algebraických doplnkov

\\ begin (zarovnaný) & A_ (11) \u003d (- 1) ^ 2 \\ cdot 8 \u003d 8; \\; A_ (12) \u003d (- 1) ^ 3 \\ cdot 9 \u003d -9; \\\\ & A_ (21) \u003d (- 1) ^ 3 \\ cdot 7 \u003d -7; \\; A_ (22) \u003d (- 1) ^ 4 \\ cdot (-5) \u003d - 5. \\\\ \\ end (zarovnané)

Z algebraických doplnkov zostavíme maticu: $ A ^ (*) \u003d \\ left (\\ begin (array) (cc) 8 & -9 \\\\ -7 & -5 \\ end (array) \\ right) $.

Transponujte výslednú maticu: $ (A ^ (*)) ^ T \u003d \\ left (\\ begin (array) (cc) 8 & -7 \\\\ -9 & -5 \\ end (array) \\ right) $ (výsledná matica je často označovaná ako adjunktívna alebo spriaznená matica s maticou $ A $). Pomocou vzorca $ A ^ (- 1) \u003d \\ frac (1) (\\ Delta A) \\ cdot (A ^ (*)) ^ T $ máme:

$$ A ^ (- 1) \u003d \\ frac (1) (- 103) \\ cdot \\ left (\\ begin (pole) (cc) 8 & -7 \\\\ -9 & -5 \\ end (pole) \\ vpravo) \u003d \\ left (\\ begin (array) (cc) -8/103 & 7/103 \\\\ 9/103 & 5/103 \\ end (array) \\ right) $$

Takže sa nachádza inverzná hodnota: $ A ^ (- 1) \u003d \\ left (\\ begin (array) (cc) -8/103 & 7/103 \\\\ 9/103 & 5/103 \\ end (array) \\ right) $. Na overenie pravdivosti výsledku stačí skontrolovať pravdivosť jednej z rovností: $ A ^ (- 1) \\ cdot A \u003d E $ alebo $ A \\ cdot A ^ (- 1) \u003d E $. Skontrolujme rovnosť $ A ^ (- 1) \\ cdot A \u003d E $. Aby sme s zlomkami menej pracovali, nahradíme maticu $ A ^ (- 1) $ nie v tvare $ \\ left (\\ begin (array) (cc) -8/103 & 7/103 \\\\ 9/103 & 5/103 \\ ) \\ vpravo) $:

$$ A ^ (- 1) \\ cdot (A) \u003d - \\ frac (1) (103) \\ cdot \\ left (\\ begin (pole) (cc) 8 & -7 \\\\ -9 & -5 \\ end ( pole) \\ pravé) \\ cdot \\ ľavé (\\ begin (pole) (cc) -5 & 7 \\\\ 9 & 8 \\ end (pole) \\ pravé) \u003d - \\ frac (1) (103) \\ cdot \\ ľavé ( \\ begin (array) (cc) -103 & 0 \\\\ 0 & -103 \\ end (pole) \\ right) \u003d \\ left (\\ begin (pole) (cc) 1 & 0 \\\\ 0 & 1 \\ end (pole) ) \\ vpravo) \u003d E $$

Odpoveď: $ A ^ (- 1) \u003d \\ left (\\ begin (array) (cc) -8/103 & 7/103 \\\\ 9/103 & 5/103 \\ end (array) \\ right) $.

Príklad č

Nájdite inverznú hodnotu matice $ A \u003d \\ left (\\ begin (array) (ccc) 1 & 7 & 3 \\\\ -4 & 9 & 4 \\\\ 0 & 3 & 2 \\ end (array) \\ right) $. Skontrolujte.

Začnime výpočtom determinantu matice $ A $. Determinant matice $ A $ je teda nasledovný:

$$ \\ Delta A \u003d \\ vľavo | \\ begin (pole) (kópia) 1 a 7 a 3 \\\\ -4 a 9 a 4 \\\\ 0 a 3 a 2 \\ koniec (pole) \\ vpravo | \u003d 18-36 + 56-12 \u003d 26. $$

Pretože $ \\ Delta A \\ neq 0 $, potom existuje inverzná matica, takže pokračujeme v riešení. Nájdeme algebraické doplnky každého prvku danej matice:

$$ \\ begin (zarovnané) & A_ (11) \u003d (- 1) ^ (2) \\ cdot \\ left | \\ begin (pole) (cc) 9 & 4 \\\\ 3 & 2 \\ end (pole) \\ vpravo | \u003d 6; A_ (12) \u003d (- 1) ^ (3) \\ cdot \\ doľava | \\ begin (pole) (cc) -4 & 4 \\\\ 0 & 2 \\ koniec (pole) \\ doprava | \u003d 8; \\; A_ (13) \u003d (- 1) ^ (4) \\ cdot \\ vľavo | \\ begin (pole) (cc) -4 & 9 \\\\ 0 & 3 \\ end (pole) \\ vpravo | \u003d -12; \\\\ & A_ (21) \u003d (- 1) ^ (3) \\ cdot \\ vľavo | \\ begin (pole) (cc) 7 & 3 \\\\ 3 & 2 \\ end (pole) \\ vpravo | \u003d -5; \\; A_ (22) \u003d (- 1) ^ (4) \\ cdot \\ left | \\ begin (pole) (cc) 1 & 3 \\\\ 0 & 2 \\ end (pole) \\ doprava | \u003d 2; \\; A_ (23) \u003d (- 1) ^ (5) \\ cdot \\ left | \\ begin (pole) (cc) 1 & 7 \\\\ 0 & 3 \\ end (pole) \\ doprava | \u003d -3; \\\\ & A_ (31) \u003d (- 1) ^ (4) \\ cdot \\ vľavo | \\ begin (pole) (cc) 7 & 3 \\\\ 9 & 4 \\ end (pole) \\ vpravo | \u003d 1; \\; A_ (32) \u003d (- 1) ^ (5) \\ cdot \\ doľava | \\ begin (pole) (cc) 1 & 3 \\\\ -4 & 4 \\ end (pole) \\ doprava | \u003d -16; \\; A_ (33) \u003d (- 1) ^ (6) \\ cdot \\ left | \\ begin (pole) (cc) 1 & 7 \\\\ -4 & 9 \\ end (pole) \\ vpravo | \u003d 37. \\ end (zarovnané) $$

Zložíme maticu algebraických doplnkov a transponujeme ju:

$$ A ^ * \u003d \\ left (\\ begin (pole) (ccc) 6 & 8 & -12 \\\\ -5 & 2 & -3 \\\\ 1 & -16 & 37 \\ end (pole) \\ vpravo); \\; (A ^ *) ^ T \u003d \\ left (\\ begin (array) (ccc) 6 & -5 & 1 \\\\ 8 & 2 & -16 \\\\ -12 & -3 & 37 \\ end (pole) \\ vpravo) ... $$

Pomocou vzorca $ A ^ (- 1) \u003d \\ frac (1) (\\ Delta A) \\ cdot (A ^ (*)) ^ T $ dostaneme:

$$ A ^ (- 1) \u003d \\ frac (1) (26) \\ cdot \\ left (\\ begin (pole) (ccc) 6 & -5 & 1 \\\\ 8 & 2 & -16 \\\\ -12 & - 3 a 37 \\ end (pole) \\ vpravo) \u003d \\ doľava (\\ begin (pole) (kópia) 3/13 a -5/26 a 1/26 \\\\ 4/13 a 1/13 a -8/13 \\ Takže $ A ^ (- 1) \u003d \\ left (\\ begin (array) (ccc) 3/13 & -5/26 & 1/26 \\\\ 4/13 & 1/13 & -8/13 \\\\ - 6/13 & -3/26 & 37/26 \\ end (pole) \\ vpravo) $. Na overenie pravdivosti výsledku stačí skontrolovať pravdivosť jednej z rovností: $ A ^ (- 1) \\ cdot A \u003d E $ alebo $ A \\ cdot A ^ (- 1) \u003d E $. Skontrolujme rovnosť $ A \\ cdot A ^ (- 1) \u003d E $. Aby sme s zlomkami menej pracovali, dosadíme maticu $ A ^ (- 1) $ nie v tvare $ \\ left (\\ begin (array) (ccc) 3/13 & -5/26 & 1/26 \\\\ 4/13 & 1/13 a -8/13 \\\\ -6/13 & -3/26 a 37/26 \\ end (pole) \\ vpravo) $ a v tvare $ \\ frac (1) (26) \\ cdot \\ left ( \\ begin (array) (ccc) 6 & -5 & 1 \\\\ 8 & 2 & -16 \\\\ -12 & -3 & 37 \\ end (pole) \\ vpravo) $:

$$ A \\ cdot (A ^ (- 1)) \u003d \\ left (\\ begin (pole) (ccc) 1 & 7 & 3 \\\\ -4 & 9 & 4 \\\\ 0 & 3 & 2 \\ end (pole) \\ right) \\ cdot \\ frac (1) (26) \\ cdot \\ left (\\ begin (pole) (ccc) 6 & -5 & 1 \\\\ 8 & 2 & -16 \\\\ -12 & -3 & 37 \\ (pole) \\ vpravo) \u003d \\ doľava (\\ začiatok (pole) (kópia) 1 a 0 & 0 \\\\ 0 & 1 & 0 \\\\ 0 & 0 & 1 \\ koniec (pole) \\ doprava) \u003d E $$

Kontrola bola úspešná, inverzná hodnota $ A ^ (- 1) $ bola nájdená správne.

: $ A ^ (- 1) \u003d \\ left (\\ begin (array) (ccc) 3/13 & -5/26 & 1/26 \\\\ 4/13 & 1/13 & -8/13 \\\\ -6 / 13 & -3/26 & 37/26 \\ end (pole) \\ vpravo) $.

OdpoveďPríklad č

Nájdite inverznú hodnotu $ A \u003d \\ left (\\ begin (array) (cccc) 6 & -5 & 8 & 4 \\\\ 9 & 7 & 5 & 2 \\\\ 7 & 5 & 3 & 7 \\\\ -4 & 8 & -8 & -3 \\ end (pole) \\ vpravo) $.

Pre maticu štvrtého rádu je nájdenie inverznej matice pomocou algebraických doplnkov do istej miery náročné. Takéto príklady v

kontrolné práce stretnúť. Ak chcete nájsť inverznú závislosť matice, musíte najskôr vypočítať determinant matice $ A $. Najlepším spôsobom, ako to v tejto situácii urobiť, je rozšírenie determinantu o riadok (stĺpec). Vyberieme ľubovoľný riadok alebo stĺpec a nájdeme algebraické doplnky každého prvku vybratého riadku alebo stĺpca.

Napríklad pre prvý riadok dostaneme:

{!LANG-ae0554f2e1ca7b6b70dcfc955ac2e5a4!}

$$ A_ (11) \u003d \\ left | \\ begin (pole) (ccc) 7 & 5 & 2 \\\\ 5 & 3 & 7 \\\\ 8 & -8 & -3 \\ end (pole) \\ vpravo | \u003d 556; \\; A_ (12) \u003d - \\ doľava | \\ begin (pole) (kópia) 9 a 5 & 2 \\\\ 7 & 3 & 7 \\\\ -4 & -8 & -3 \\ end (pole) \\ doprava | \u003d -300 ; $$ $$ A_ (13) \u003d \\ doľava | \\ begin (pole) (kópia) 9 a 7 & 2 \\\\ 7 & 5 & 7 \\\\ -4 & 8 & -3 \\ end (pole) \\ doprava | \u003d -536; A_ (14) \u003d - \\ doľava | \\ begin (pole) (kópia) 9 a 7 & 5 \\\\ 7 & 5 & 3 \\\\ -4 & 8 & -8 \\ end (pole) \\ doprava | \u003d -112. $$

Determinant matice $ A $ sa vypočíta podľa tohto vzorca:

$$ \\ Delta (A) \u003d a_ (11) \\ cdot A_ (11) + a_ (12) \\ cdot A_ (12) + a_ (13) \\ cdot A_ (13) + a_ (14) \\ cdot A_ (14) ) \u003d 6 \\ cdot 556 + (- 5) \\ cdot (-300) +8 \\ cdot (-536) +4 \\ cdot (-112) \u003d 100. $$

$$ \\ begin (zarovnané) & A_ (21) \u003d - 77; \\; A_ (22) \u003d 50; \\; A_ (23) \u003d 87; \\; A_ (24) \u003d 4; \\\\ & A_ (31) \u003d -93; \\; A_ (32) \u003d 50; \\; A_ (33) \u003d 83; \\; A_ (34) \u003d 36; \\\\ & A_ (41) \u003d 473; \\; A_ (42) \u003d - 250 ; \\; A_ (43) \u003d - 463; \\; A_ (44) \u003d - 96. \\ end (zarovnané) $$

Algebraická komplementárna matica: $ A ^ * \u003d \\ left (\\ begin (array) (cccc) 556 & -300 & -536 & -112 \\\\ -77 & 50 & 87 & 4 \\\\ -93 & 50 & 83 & 36 \\\\ 473 & -250 & -463 & -96 \\ end (pole) \\ vpravo) $.

Pripojená matica: $ (A ^ *) ^ T \u003d \\ left (\\ begin (array) (cccc) 556 & -77 & -93 & 473 \\\\ -300 & 50 & 50 & -250 \\\\ -536 & 87 & 83 & -463 \\\\ -112 & 4 & 36 & -96 \\ end (pole) \\ vpravo) $.

Inverzná matica:

$$ A ^ (- 1) \u003d \\ frac (1) (100) \\ cdot \\ left (\\ begin (pole) (cccc) 556 & -77 & -93 & 473 \\\\ -300 & 50 & 50 & -250 \\\\ -536 & 87 & 83 & -463 \\\\ -112 & 4 & 36 & -96 \\ end (array) \\ right) \u003d \\ left (\\ begin (array) (cccc) 139/25 & -77/100 & -93/100 & 473/100 \\\\ -3 & 1/2 & 1/2 & -5/2 \\\\ -134/25 & 87/100 & 83/100 & -463/100 \\\\ -28 / 25 & 1/25 & 9/25 & -24/25 \\ end (pole) \\ vpravo) $$

Kontrola, ak je to žiaduce, sa môže vykonať rovnakým spôsobom ako v predchádzajúcich príkladoch.

Odpoveď: $ A ^ (- 1) \u003d \\ left (\\ begin (array) (cccc) 139/25 & -77/100 & -93/100 & 473/100 \\\\ -3 & 1/2 & 1/2 & -5/2 \\\\ -134/25 & 87/100 & 83/100 & -463/100 \\\\ -28/25 & 1/25 & 9/25 & -24/25 \\ end (pole) \\ vpravo) $.

V druhej časti sa budeme zaoberať iným spôsobom hľadania inverznej matice, ktorý spočíva v použití transformácií Gaussovej metódy alebo Gauss-Jordanovej metódy.