Finding the reverse. Find a reverse matrix online. Algebraic supplements and minors

1. Find the determinant of the initial matrix. If, the matrix is \u200b\u200bdegenerate and the return matrix exists. If, then the matrixiane and reverse matrix exists.

2. Find a matrix transposed to.

3. We find algebraic additions of elements and make up of them an attached matrix.

4. Make a reverse matrix by the formula.

5. We check the correctness of the calculation of the reverse matrix, based on its definition:.

Example.Find the matrix inverse this :.

Decision.

1) the determinant of the matrix

.

2) we find algebraic supplements of the elements of the matrix and make an attached matrix:

3) Calculate the reverse matrix:

,

4) Check:

№4 Rank matrix. Linear independence of the lines of the matrix

To solve and research a number of mathematical and applied tasks, the concept of the grade of the matrix is \u200b\u200bimportant.

In the matrix, the size of any rows and columns can be pulled out square browsing-order, where. The determinants of such reviews are called miners -o order matrix .

For example, from the matrices, you can get browsing 1, 2 and 3rd order.

Definition. The rag of the matrix is \u200b\u200bthe highest order of different minors of this matrix different from zero. Designation: or.

From the definition follows:

1) the rank of the matrix does not exceed a smaller size, i.e.

2) if and only when all the elements of the matrix are zero, i.e.

3) for the square matrix of the N-th order if and only when the matrix is \u200b\u200bnondegenerate.

Since the direct bust of all possible minors of the matrix, starting with the greatest size, is difficult (labor-intensives), they use elementary matrix transformations that retain the grade of the matrix.

Elementary matrix conversion:

1) Returning the zero line (column).

2) multiplying all row elements (column) by number.

3) Changing the order of strings (columns) of the matrix.

4) Adjustment to each element of one line (column) of the corresponding elements of another line (column) multiplied by any number.

5) Transposing the matrix.

Definition. The matrix obtained from the matrix of the help of elementary transformations is called equivalent and indicated BUT IN.

Theorem. The ring of the matrix does not change during elementary matrix transformations.

With the help of elementary transformations, you can bring the matrix to the so-called step type, when the calculation of its rank is not difficult.

The matrix is \u200b\u200bcalled a stepwise if it looks like:

Obviously, the rank of the stepped matrix is \u200b\u200bequal to the number of nonzero strings, because There is a minor order, not equal to zero:

.

Example. Determine the rag of the matrix using elementary transformations.

The rank of the matrix is \u200b\u200bequal to the number of nonzero strings, i.e. .

№5Linear independence of the lines of the matrix

Dana sized matrix

Denote the string of the matrix as follows:

Two lines are called equal If their corresponding elements are equal. .

We introduce the multiplication operations of the string to the number and addition of strings as an operation carried out alternately:

Definition. The string is called a linear combination of the line, if it is equal to the amount of works of these lines to arbitrary valid numbers (any numbers):

Definition. Rows of the matrix are called linearly dependent if there are numbers that are not equal at the same time zero that the linear combination of the matrix rows is equal to the zero line:

Where. (1.1)

The linear dependence of the matrix strings denotes that at least 1 string of the matrix is \u200b\u200ba linear combination of the remaining.

Definition. If the linear combination of strings (1.1) is zero if and only if all coefficients, then row linearly independent .

Matrix Range Theorem . The grade rank of the matrix is \u200b\u200bequal to the maximum number of its linearly independent rows or columns, through which all other lines (columns) are linearly expressed.

Theorem plays a fundamental role in matrix analysis, in particular, in the study of systems linear equations.

№6 Solution of the system of linear equations SN

Linear equations are widely used in the economy.

The system of linear equations is interconnected with the form:

,

where () - arbitrary numbers called coefficients with variables and free members of equations , respectively.

Summary: ().

Definition. The solution by the system is called such a set of values, when substituting which each equation of the system appeals to the right equality.

1) the system of equations is called joint if it has at least one solution and non-stopif it does not have solutions.

2) the joint system of equations is called defined if it has the only solution and uncertain if it has more than one solution.

3) two systems of equations are called equivalent (equivalent ) If they have the same set of solutions (for example, one solution).

The inverse matrix for this is such a matrix, multiplying the initial to which the unit matrix gives: mandatory and sufficient condition The presence of a reverse matrix is \u200b\u200bthe inequality zero determinant source (which in turn implies that the matrix must be square). If the determinant of the matrix is \u200b\u200bzero, it is called degenerate and such a matrix has no reverse. In higher mathematics, inverse matrices are important and used to solve a number of tasks. For example, on finding the return matrix A matrix method of solving systems of equations was constructed. Our service site allows calculate the return matrix online Two methods: by Gauss-Jordan and with the help of a matrix of algebraic add-ons. Intersching implies a large number of elementary transformations inside the matrix, the second is the calculation of the determinant and algebraic additions to all elements. To calculate the identifier of the matrix online, you can use the other our service - calculating the determinant of the matrix online

Find a reverse matrix to the site

website Allows you to find reverse matrix online Quickly and free. The site makes the computing by our service and is issued a result with a detailed decision on finding reverse matrix. The server always gives only an accurate and correct answer. In tasks by definition reverse matrix online, it is necessary to determine matrians was different from zero, otherwise website Reporting the inability to find the inverse matrix due to the equality zero of the determinant of the original matrix. Task for finding reverse matrix It is found in many sections of mathematics, being one of the most basic concepts of algebra and a mathematical instrument in applied tasks. Self determination of the return matrix requires considerable effort, a lot of time, calculations and great care, to prevent a list or small error in computing. Therefore, our service on finding the return matrix online Significantly alleviates you the task and will become an indispensable tool for solving mathematical problems. Even if you find a reverse matrix Alone, we recommend checking your decision on our server. Enter your original matrix with us to calculate the reverse matrix online and deposit your answer. Our system is never mistaken and finds reverse matrix specified dimension in mode online instantly! Online website Symbolic records are allowed in elements. matrix, in this case reverse matrix online will be presented in general symbol.

Algebraic supplements and minors

Let them have a third-order determinant: .

Minorcorresponding to this element a ij. The determinant of the third order is called the second order determinant obtained from this line with the string and the column, at the intersection of which this element is worth it, i.e. i.Line I. j.-to column. Minors relevant to this element a ij. We will denote M ij..

for example, Minor M 12.corresponding to the element a 12.will be determined 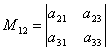which is obtained by trimming from this determinant of the 1st line and the 2nd column.

Thus, the formula defining the third order determination shows that this determinant is equal to the amount of works of elements of the 1st line to the corresponding minors; At the same time, minor corresponding to the element a 12., takes about the sign "-", i.e. You can record that

Similarly, you can enter the definitions of minors for the determinants of the second order and higher orders.

We introduce another concept.

Algebraic supplementelement a ij. The determinant is called His Minor M ij.multiplied by (-1) i + j.

Algebraic supplement element a ij. denotes A ij..

From the definition we obtain that the connection between the algebraic supplement of the element and its minor is expressed by equality A ij. \u003d (-1) i + j M ij.

For example,

Example. Data determined. To find A 13, A 21, A 32.

It is easy to see that using algebraic supplements of elements, formula (1) can be written as:

Similarly to this formula, you can obtain a decomposition of the determinant on the items of any row or column.

For example, the decomposition of the determinant for the elements of the 2nd string can be obtained as follows. According to the 2 property of the determinant, we have:

Spread the resulting determinant for elements of the 1st line.

.

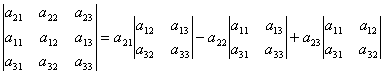(2)

From here Because Second-order determinants in the formula (2) are minors elements a 21, A 22, A 23. Thus, i.e. We received a decomposition of the determinant for the elements of the 2nd row.

Similarly, it is possible to obtain a decomposition of the determinant for third-line elements. Using the property of 1 identifiers (about transposing), it can be shown that similar decompositions are valid and decomposed by elements of columns.

Thus, the following theorem is valid.

Theorem (on the decomposition of the determinant for a specified row or column). The determinant is equal to the amount of the works of the elements of any of its row (or column) on their algebraic additions.

All of the above is valid for the determinants of any higher order.

Examples.

INVERSE MATRIX

The concept of the return matrix is \u200b\u200bentered only for square matrices.

If a A. - square matrix, then inverse For her, the matrix is \u200b\u200bcalled the matrix, denoted A -1. and satisfying condition. (This definition is entered by analogy with multiplication of numbers)

In this article we will talk about the matrix method of solving a system of linear algebraic equations, we will find its definition and give examples of the solution.

Definition 1.

Reverse matrix method - This is a method used in solving a slope if the number of unknown is equal to the number of equations.

Example 1.

Find the solution of the system N of linear equations with n unknown:

a 11 x 1 + A 12 x 2 +. . . + a 1 n x n \u003d b 1 a n 1 x 1 + a n 2 x 2 +. . . + a n n x n \u003d b n

Matrix recording type : A × x \u003d b

where A \u003d A 11 A 12 ⋯ A 1 N A 21 A 22 ⋯ A 2 N ⋯ ⋯ ⋯ ⋯ A N 1 A N 2 ⋯ A N n is the system matrix.

X \u003d x 1 x 2 ⋮ x n - column of unknown,

B \u003d B 1 b 2 ⋮ B n - column of free coefficients.

From the equation that we received must be expressed x. To do this, multiply both parts of the matrix equation on the left to A - 1:

A - 1 × a × x \u003d a - 1 × b.

Since a - 1 × a \u003d e, then e × x \u003d a - 1 × in or x \u003d a - 1 × V.

Comment

The inverse matrix to the matrix A has the right to exist only if the condition D E T A N E R A N E N N YOU. Therefore, when solving the slam by the method of inverse matrix, first of all is D E T A.

In the event that D E T A N E P A N E N NUT, the system has only one solution option: using the reverse matrix method. If D e \u200b\u200bt a \u003d 0, then the system cannot be solved by this method.

An example of solving a system of linear equations using a reverse matrix method

We solve the slave by the method of inverse matrix:

2 x 1 - 4 x 2 + 3 x 3 \u003d 1 x 1 - 2 x 2 + 4 x 3 \u003d 3 3 x 1 - x 2 + 5 x 3 \u003d 2

How to solve?

• Record the system in the form of a matrix equation A x \u003d b, where

A \u003d 2 - 4 3 1 - 2 4 3 - 1 5, x \u003d x 1 x 2 x 3, b \u003d 1 3 2.

• Express from this equation X:

• We find the determinant of the matrix A:

det a \u003d 2 - 4 3 1 - 2 4 3 - 1 5 \u003d 2 × (- 2) × 5 + 3 × (- 4) × 4 + 3 × (- 1) × 1 - 3 × (- 2) × 3 - - 1 × (- 4) × 5 - 2 × 4 - (- 1) \u003d - 20 - 48 - 3 + 18 + 20 + 8 \u003d - 25

d E T is not equal to 0, therefore for this system suits the method of solving the inverse matrix.

• We find the inverse matrix A - 1 with the help of an allied matrix. Calculate algebraic additions A I J to the corresponding elements of the matrix A:

A 11 \u003d (- 1) (1 + 1) - 2 4 - 1 5 \u003d - 10 + 4 \u003d - 6,

A 12 \u003d (- 1) 1 + 2 1 4 3 5 \u003d - (5 - 12) \u003d 7,

And 13 \u003d (- 1) 1 + 3 1 - 2 3 - 1 \u003d - 1 + 6 \u003d 5,

A 21 \u003d (- 1) 2 + 1 - 4 3 - 1 5 \u003d - (- 20 + 3) \u003d 17,

And 22 \u003d (- 1) 2 + 2 2 3 3 5 - 10 - 9 \u003d 1,

And 23 \u003d (- 1) 2 + 3 2 - 4 3 - 1 \u003d - (- 2 + 12) \u003d - 10,

A 31 \u003d (- 1) 3 + 1 - 4 3 - 2 4 \u003d - 16 + 6 \u003d - 10,

And 32 \u003d (- 1) 3 + 2 2 3 1 4 \u003d - (8 - 3) \u003d - 5,

A 33 \u003d (- 1) 3 + 3 2 - 4 1 - 2 \u003d - 4 + 4 \u003d 0.

• We write down the allied matrix A *, which is composed of algebraic supplements of the matrix A:

A * \u003d - 6 7 5 17 1 - 10 - 10 - 5 0

• Record the inverse matrix according to the formula:

A - 1 \u003d 1 D E T A (A *) T: A - 1 \u003d - 1 25 - 6 17 - 10 7 1 - 5 5 - 10 0,

• We multiply a reverse matrix A - 1 on a column of free members in and we get a solution of the system:

X \u003d a - 1 × b \u003d - 1 25 - 6 17 - 10 7 1 - 5 5 - 10 0 1 3 2 \u003d - 1 25 - 6 + 51 - 20 7 + 3 - 10 5 - 30 + 0 \u003d - 1 0 1.

Answer : x 1 \u003d - 1; x 2 \u003d 0; x 3 \u003d 1

If you notice a mistake in the text, please select it and press Ctrl + Enter

The matrix $ A ^ (- 1) $ is called reverse with respect to the square matrix $ a $ if the condition $ A ^ (- 1) \\ Cdot A \u003d A \\ Cdot A ^ (- 1) \u003d E $, where $ E $ - a single matrix, the order of which is equal to the order of the matrix $ a $.

Non-degenerate matrix - matrix, the determinant of which is not equal to zero. Accordingly, the degenerate matrix is \u200b\u200bthe one in which the determinant is zero.

The reverse matrix $ A ^ (- 1) $ exists if and only when the matrix $ a $ is nondegenerate. If the reverse matrix $ a ^ (- 1) $ exists, then it is the only one.

There are several ways to find a reverse matrix, and we will look at two of them. On this page, the method of an attached matrix will be considered, which relies as standard in most courses of higher mathematics. The second method of finding the reverse matrix (the method of elementary transformations), which involves the use of the Gauss method or the Gauss-Jordan method, is considered in the second part.

The method of attached (allied) matrix

Let the matrix of $ A_ (N \\ Times N) $. In order to find a reverse matrix $ a ^ (- 1) $, it is required to carry out three steps:

1. Find the identifier of the matrix $ a $ and make sure that $ \\ Delta A \\ NEQ 0 $, i.e. that the matrix A is nondegenerate.
2. Create algebraic supplements $ a_ (ij) $ of each element of the $ A $ matrix and burn the $ a_ matrix (n \\ Times N) ^ (*) \u003d \\ left (A_ (IJ) \\ Right) $ from the found algebraic additions.
3. Record the inverse matrix with regard to the formula $ A ^ (- 1) \u003d \\ FRAC (1) (\\ Delta A) \\ Cdot (A ^ (*)) ^ T $.

The $ matrix (a ^ (*)) ^ t $ is often referred to as the attached (mutual, allied) to the $ a $ matrix.

If the solution occurs manually, the first method is good only for matrices of relatively small orders: the second (), third (), fourth (). To find a reverse matrix for the highest order matrix, other methods are used. For example, the Gauss method, which is considered in the second part.

Example №1

Find the matrix back to the matrix $ a \u003d \\ left (\\ begin (Array) (CCCC) 5 & -4 & 1 & 0 \\\\ 12 & -11 & 4 & 0 \\\\ -5 & 58 & 4 & 0 \\\\ 3 & - 1 & -9 & 0 \\ END (Array) \\ Right) $.

Since all elements of the fourth column are zero, then $ \\ delta a \u003d 0 $ (i.e., the $ a $ matrix is \u200b\u200bdegenerate). Since $ \\ delta a \u003d 0 $, then the reverse matrix to the $ a $ matrix does not exist.

Answer: Matrix $ A ^ (- 1) $ does not exist.

Example number 2.

Find a matrix back to the matrix $ a \u003d \\ left (\\ Begin (Array) (CC) -5 & 7 \\\\ 9 & 8 \\ END (Array) \\ Right) $. Perform check.

Use the method of the attached matrix. We will find the determinant of a given matrix $ a $:

$$ \\ Delta A \u003d \\ Left | \\ Begin (Array) (CC) -5 & 7 \\\\ 9 & 8 \\ END (Array) \\ Right | \u003d -5 \\ CDOT 8-7 \\ CDOT 9 \u003d -103. $$.

Since $ \\ Delta A \\ NEQ 0 $, the reverse matrix exists, therefore will continue the solution. We find algebraic add-ons

\\ begin (aligned) & a_ (11) \u003d (- 1) ^ 2 \\ Cdot 8 \u003d 8; \\; A_ (12) \u003d (- 1) ^ 3 \\ Cdot 9 \u003d -9; \\\\ & A_ (21) \u003d (- 1) ^ 3 \\ Cdot 7 \u003d -7; \\; A_ (22) \u003d (- 1) ^ 4 \\ Cdot (-5) \u003d - 5. \\\\ \\ END (Aligned)

We make a matrix of algebraic additions: $ a ^ (*) \u003d \\ left (\\ begin (array) (CC) 8 & -9 \\\\ -7 & -5 \\ END (Array) \\ Right) $.

We transform the resulting matrix: $ (a ^ (*)) ^ t \u003d \\ left (\\ begin (array) (CC) 8 & -7 \\\\ -9 & -5 \\ END (Array) \\ Right) $ (the resulting matrix often It is referred to as the attached or allied matrix to the matrix $ a $). Using the formula $ A ^ (- 1) \u003d \\ FRAC (1) (\\ Delta A) \\ CDOT (A ^ (*)) ^ T $, we have:

$$ a ^ (- 1) \u003d \\ FRAC (1) (- 103) \\ CDOT \\ LEFT (\\ Begin (Array) (CC) 8 & -7 \\\\ -9 & -5 \\ END (Array) \\ Right) \u003d \\ Left (\\ Begin (Array) (CC) -8/103 & 7/103 \\\\ 9/103 & 5/103 \\ END (Array) \\ Right) $$

So, the reverse matrix is \u200b\u200bfound: $ a ^ (- 1) \u003d \\ left (\\ begin (array) (CC) -8/103 & 7/103 \\\\ 9/103 & 5/103 \\ END (Array) \\ Right) $. To check the truth of the result, it is enough to check the truth of one of the equals: $ a ^ (- 1) \\ Cdot a \u003d e $ or $ A \\ Cdot A ^ (- 1) \u003d E $. We check the implementation of the equality $ a ^ (- 1) \\ Cdot a \u003d e $. In order to work less with fractions, we will substitute the $ a ^ matrix (- 1) $ not in the form of $ \\ left (\\ begin (array) (CC) -8/103 & 7/103 \\\\ 9/103 & 5/103 \\ ) \\ Right) $:

$$ a ^ (- 1) \\ Cdot (a) \u003d - \\ FRAC (1) (103) \\ CDOT \\ Left (\\ Begin (Array) (CC) 8 & -7 \\\\ -9 & -5 \\ END ( Array) \\ Right) \\ CDOT \\ LEFT (\\ Begin (Array) (CC) -5 & 7 \\\\ 9 & 8 \\ END (Array) \\ Right) \u003d - \\ FRAC (1) (103) \\ CDOT \\ LEFT ( \\ Begin (Array) (CC) -103 & 0 \\\\ 0 & -103 \\ END (Array) \\ Right) \u003d \\ Left (\\ Begin (Array) (CC) 1 & 0 \\\\ 0 & 1 \\ END (Array ) \\ RIGHT) \u003d E $$

Answer: $ A ^ (- 1) \u003d \\ left (\\ begin (array) (CC) -8/1033 & 7/103 \\\\ 9/103 & 5/103 \\ END (Array) \\ Right) $.

Example number 3.

Find a reverse matrix for the $ a \u003d \\ left matrix (\\ begin (Array) (CCC) 1 & 7 & 3 \\\\ -4 & 9 & 4 \\\\ 0 & 3 & 2 \\ END (Array) \\ Right) $. Perform check.

Let's start with the calculation of the identifier of the matrix $ a $. So, the identifier of the matrix $ a $ is:

$$ \\ Delta A \u003d \\ Left | \\ Begin (Array) (CCC) 1 & 7 & 3 \\\\ -4 & 9 & 4 \\\\ 0 & 3 & 2 \\ End (Array) \\ Right | \u003d 18-36 + 56-12 \u003d 26. $$.

Since $ \\ Delta A \\ NEQ 0 $, the reverse matrix exists, therefore will continue the solution. We find algebraic additions to each element of a given matrix:

$$ \\ Begin (Aligned) & A_ (11) \u003d (- 1) ^ (2) \\ CDOT \\ LEFT | \\ Begin (Array) (CC) 9 & 4 \\\\ 3 & 2 \\ END (Array) \\ RIGHT | \u003d 6; \\; A_ (12) \u003d (- 1) ^ (3) \\ CDOT \\ LEFT | \\ Begin (Array) (CC) -4 & 4 \\\\ 0 \\ END (Array) \\ Right | \u003d 8; \\; A_ (13) \u003d (- 1) ^ (4) \\ Cdot \\ Left | \\ Begin (Array) (CC) -4 & 9 \\\\ 0 & 3 \\ ED (Array) \\ Right | \u003d -12; \\\\ & A_ (21) \u003d (- 1) ^ (3) \\ CDOT \\ LEFT | \\ Begin (Array) (CC) 7 & 3 \\\\ 3 \\ END (Array) \\ Right | \u003d -5; \\; A_ (22) \u003d (- 1) ^ (4) \\ Cdot \\ left | \\ begin (array) (CC) 1 & 3 \\\\ 0 \\ END (Array) \\ Right | \u003d 2; \\; A_ (23) \u003d (- 1) ^ (5) \\ CDOT \\ LEFT | \\ Begin (Array) (CC) 1 & 7 \\\\ 0 & 3 \\ END (Array) \\ Right | \u003d -3; \\\\ & A_ (31) \u003d (- 1) ^ (4) \\ CDOT \\ LEFT | \\ Begin (Array) (CC) 7 & 3 \\\\ 9 & 4 \\ END (Array) \\ Right | \u003d 1; \\; A_ (32) \u003d (- 1) ^ (5) \\ CDOT \\ LEFT | \\ Begin (Array) (CC) 1 & 3 \\\\ -4 & 4 \\ END (Array) \\ Right | \u003d -16; \\; A_ (33) \u003d (- 1) ^ (6) \\ CDOT \\ LEFT | \\ Begin (Array) (CC) 1 & 7 \\\\ -4 & 9 \\ END (Array) \\ Right | \u003d 37. \\ End (Aligned) $$

We make a matrix from algebraic additions and transparency it:

$$ A ^ * \u003d \\ Left (\\ Begin (Array) (CCC) 6 & 8 & -12 \\\\ -5 & 2 & -3 \\ END & -16 & 37 \\ END (Array) \\ Right); \\; (A ^ *) ^ T \u003d \\ Left (\\ Begin (Array) (CCC) 6 & -5 & 1 \\\\ 8 & 2 & -16 \\\\ -12 & -3 & 37 \\ END (Array) \\ Right) . $$.

Using the formula $ A ^ (- 1) \u003d \\ FRAC (1) (\\ Delta A) \\ Cdot (A ^ (*)) ^ T $, we get:

$$ A ^ (- 1) \u003d \\ FRAC (1) (26) \\ CDOT \\ LEFT (\\ Begin (Array) (CCC) 6 & -5 & 1 \\\\8 & \u200b\u200b2 & -16 \\\\ -12 & - 3 & 37 \\ END (Array) \\ Right) \u003d \\ Left (\\ Begin (Array) (CCC) 3/13 & -5/26 & 1/26 \\\\ 4/13 & 1/13 & -8/13 \\ So, $ A ^ (- 1) \u003d \\ Left (\\ Begin (Array) (CCC) 3/13 & -5/26 & 1/26 \\\\ 4/13 & 1/13 & -8/13 \\\\ - 6/13 & -3/26 & 37/26 \\ END (Array) \\ Right) $. To check the truth of the result, it is enough to check the truth of one of the equals: $ a ^ (- 1) \\ Cdot a \u003d e $ or $ A \\ Cdot A ^ (- 1) \u003d E $. Check the implementation of the equality $ a \\ cdot a ^ (- 1) \u003d E $. So less work with fractions, we will substitute the $ a ^ matrix (- 1) $ not in the form of $ \\ left (\\ begin (array) (CCC) 3/13 & -5/26 & 1/26 \\\\ 4/13 & 1/13 & -8/13 \\\\ -6/13 & -3/26 & 37/26 \\ END (Array) \\ Right) $, and in the form $ \\ FRAC (1) (26) \\ CDOT \\ LEFT ( \\ Begin (Array) (CCC) 6 & -5 & 1 \\\\ 8 & 2 & -16 \\\\ -12 & -3 & 37 \\ END (Array) \\ Right) $:

$$ A \\ CDOT (A ^ (- 1)) \u003d \\ Left (\\ Begin (Array) (CCC) 1 & 7 & 3 \\\\ -4 & 9 & 4 \\\\ 0 & 3 & 2 \\ END (Array) \\ Right) \\ CDOT \\ FRAC (1) (26) \\ CDOT \\ LEFT (\\ Begin (Array) (CCC) 6 & -5 & 1 \\\\ 8 & 2 & -16 \\\\ -12 & -3 & 37 \\ (Array) \\ Right) \u003d \\ Left (\\ Begin (Array) (CCC) 1 & 0 & 0 \\\\ 0 & 1 & 0 \\\\ 0 & 0 & 1 \\ END (Array) \\ Right) \u003d E $$

The check was completed successfully, the reverse matrix $ a ^ (- 1) $ is found correctly.

: $ A ^ (- 1) \u003d \\ left (\\ begin (array) (CCC) 3/13 & -5/26 & 1/26 \\\\ 4/13 & 1/13 & -8/13 \\\\ -6 / 13 & -3/26 & 37/26 \\ END (Array) \\ Right) $.

AnswerExample number 4.

Find a matrix, reverse matrix $ a \u003d \\ left (\\ Begin (Array) (CCCC) 6 & -5 & 8 & 4 \\\\ 9 & 7 & 5 & 2 \\\\ 7 & 5 & 3 & 7 \\\\ -4 & 8 & -8 & -3 \\ END (Array) \\ Right) $.

For the fourth order matrix, finding a reverse matrix with algebraic additions is somewhat difficult. However, such examples in

test work meet. To find a reverse matrix, first you need to calculate the identifier of the $ a $ matrix. It is best to do this in this situation with the decomposition of the definition on a string (column). Choose any string or column and find algebraic additions to each element of the selected line or column.

For example, for the first line we will get:

$$ A_ (11) \u003d \\ left | \\ begin (Array) (CCC) 7 & 5 & 2 \\\\ 5 & 3 & 7 \\\\ 8 & -8 & -3 \\ END (Array) \\ Right | \u003d 556; \\; A_ (12) \u003d - \\ Left | \\ Begin (Array) (CCC) 9 & 5 & 2 \\\\ 7 & 3 & 7 \\\\ -4 & -8 & 3 \\ END (Array) \\ Right | \u003d -300 ; $$$$ A_ (13) \u003d \\ left | \\ begin (Array) (CCC) 9 & 7 & 2 \\\\ 7 & 5 & 7 \\\\ -4 & 8 & -3 \\ END (Array) \\ Right | \u003d -536; \\; A_ (14) \u003d - \\ Left | \\ Begin (Array) (CCC) 9 & 7 & 5 \\\\ 7 & 5 & 3 \\\\ -4 & 8 & -8 \\ END (Array) \\ Right | \u003d -112. $$.

The identifier of the matrix of $ a $ will calculate according to the following formula:

$$ \\ DELTA (a) \u003d a_ (11) \\ Cdot A_ (11) + A_ (12) \\ CDOT A_ (12) + A_ (13) \\ CDOT A_ (13) + A_ (14) \\ Cdot A_ (14 ) \u003d 6 \\ CDOT 556 + (- 5) \\ Cdot (-300) +8 \\ Cdot (-536) +4 \\ CDOT (-112) \u003d 100. $$.

$$ \\ Begin (Aligned) & A_ (21) \u003d - 77; \\; A_ (22) \u003d 50; \\; A_ (23) \u003d 87; \\; A_ (24) \u003d 4; \\\\ & A_ (31) \u003d -93; \\; A_ (32) \u003d 50; \\; A_ (33) \u003d 83; \\; A_ (34) \u003d 36; \\\\ & A_ (41) \u003d 473; \\; A_ (42) \u003d - 250 ; \\; A_ (43) \u003d - 463; \\; A_ (44) \u003d - 96. \\ End (Aligned) $$

Matrix of algebraic add-ons: $ a ^ * \u003d \\ left (\\ Begin (Array) (CCCC) 556 & -300 & -536 & -112 \\\\ -77 & 50 & 87 & 4 \\\\ -93 & 50 & 83 & 36 \\\\ 473 & -46 \\ END (Array) \\ Right) $.

Attached Matrix: $ (A ^ *) ^ T \u003d \\ Left (\\ Begin (Array) (CCCC) 556 & -77 & -93 & 473 \\\\ -300 & 50 & 50 & -250 \\\\ -536 & 87 & 83 & -463 \\\\ -112 & 4 & 36 & -96 \\ END (Array) \\ Right) $.

Inverse matrix:

$$ A ^ (- 1) \u003d \\ FRAC (1) (100) \\ CDOT \\ LEFT (\\ Begin (Array) (CCCC) 556 & -77 & -93 & 473 \\\\ -300 & 50 & 50 & -250 \\\\ -536 & 87 & 83 & 463 \\\\ -112 & 4 & 36 & -96 \\ END (Array) \\ Right) \u003d \\ Left (\\ Begin (Array) (CCCC) 139/25 & -77/100 & -93/100 & 473/100 \\\\ -3 & 1/2 & 1/2 & -5/2 \\\\ -134/25 & 87/100 & 83/100 & -463/100 \\\\ -28 / 25 & 1/25 & 9/25 & -24/25 \\ End (Array) \\ Right) $$

Check, if desired, can be manufactured in the same way as in previous examples.

Answer: $ A ^ (- 1) \u003d \\ Left (\\ Begin (Array) (CCCC) 139/25 & -77/100 & -93/100 & 473/100 \\\\ -3 & 1/2 & 1/2 & -5/2 \\\\ -134/25 & 87/100 & 83/100 & -463/100 \\\\ -28/25 & 1/25 & 9/25 & -24/25 \\ END (Array) \\ Right) $.

In the second part, another method of finding a reverse matrix will be considered, which involves the use of transformations of the Gauss method or Gaussa-Jordan method.