Propiedades del tetraedro, tipos y fórmulas. Volumen de un tetraedro Dibujo de tetraedro regular

Tetraedro traducido del griego significa "tetraedro". Esta figura geométrica tiene cuatro caras, cuatro vértices y seis aristas. Las caras son triángulos. De hecho, el tetraedro es la primera mención de poliedros que apareció mucho antes de la existencia de Platón.

Hoy hablaremos sobre los elementos y propiedades del tetraedro y también aprenderemos las fórmulas para encontrar el área, el volumen y otros parámetros de estos elementos.

Elementos de un tetraedro

Un segmento extraído de cualquier vértice de un tetraedro y dejado caer hasta el punto de intersección de las medianas de la cara opuesta se llama mediana.

La altura de un polígono es un segmento normal trazado desde el vértice opuesto.

Una bimediana es un segmento que conecta los centros de los bordes que se cruzan.

Propiedades del tetraedro

1) Los planos paralelos que pasan por dos aristas que se cruzan forman un paralelepípedo circunscrito.

2) Una propiedad distintiva de un tetraedro es que las medianas y bimedianas de la figura se encuentran en un punto. Es importante que este último divida las medianas en una proporción de 3:1 y las bimedianas por la mitad.

3) Un plano divide un tetraedro en dos partes de igual volumen si pasa por el medio de dos aristas que se cruzan.

Tipos de tetraedro

La diversidad de especies de la figura es bastante amplia. Un tetraedro puede ser:

• regular, es decir, en la base un triángulo equilátero;
• isoédrico, en el que todas las caras tienen la misma longitud;
• ortocéntrica, cuando las alturas tienen un punto de intersección común;
• rectangular si los ángulos planos en el vértice son normales;
• proporcional, todas las alturas bi son iguales;
• marco si hay una esfera que toca las costillas;
• incéntrico, es decir, los segmentos que caen desde el vértice hasta el centro del círculo inscrito de la cara opuesta tienen un punto de intersección común; este punto se llama centro de gravedad del tetraedro.

Detengámonos en detalle en el tetraedro regular, cuyas propiedades son prácticamente las mismas.

Según el nombre, puedes entender que se llama así porque las caras son triángulos regulares. Todas las aristas de esta figura son congruentes en longitud y las caras son congruentes en área. Un tetraedro regular es uno de cinco poliedros similares.

Fórmulas de tetraedro

La altura de un tetraedro es igual al producto de la raíz de 2/3 por la longitud de la arista.

El volumen de un tetraedro se encuentra de la misma forma que el volumen de una pirámide: la raíz cuadrada de 2 dividida por 12 y multiplicada por la longitud de la arista del cubo.

Las fórmulas restantes para calcular el área y los radios de círculos se presentan arriba.

Considere un triángulo arbitrario ABC y un punto D que no se encuentra en el plano de este triángulo. Conectemos este punto con los vértices del triángulo ABC usando segmentos. Como resultado, obtenemos los triángulos ADC, CDB, ABD. La superficie delimitada por cuatro triángulos ABC, ADC, CDB y ABD se llama tetraedro y se denomina DABC.
Los triángulos que forman un tetraedro se llaman caras.
Los lados de estos triángulos se llaman aristas del tetraedro. Y sus vértices son los vértices de un tetraedro.

El tetraedro tiene 4 caras, 6 costillas Y 4 picos.
Dos aristas que no tienen un vértice común se llaman opuestas.
A menudo, por conveniencia, una de las caras de un tetraedro se llama base, y las tres caras restantes son caras laterales.

Por tanto, un tetraedro es el poliedro más simple cuyas caras son cuatro triángulos.

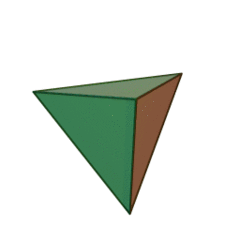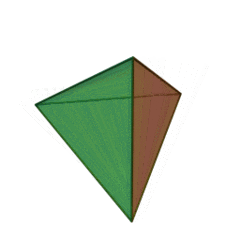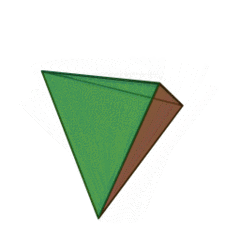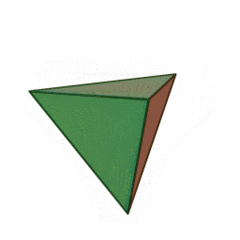Pero también es cierto que cualquier pirámide triangular arbitraria es un tetraedro. Entonces también es cierto que un tetraedro se llama una pirámide con un triángulo en su base.

Altura del tetraedro Se llama segmento al que une un vértice con un punto situado en la cara opuesta y perpendicular a él.
Mediana de un tetraedro Se llama segmento que conecta un vértice con el punto de intersección de las medianas de la cara opuesta.
Bimediana de un tetraedro llamado segmento que conecta los puntos medios de los bordes que se cruzan de un tetraedro.

Dado que un tetraedro es una pirámide con base triangular, el volumen de cualquier tetraedro se puede calcular mediante la fórmula

• S– área de cualquier cara,
• h– altura bajada a esta cara

Tetraedro regular: un tipo especial de tetraedro

Un tetraedro en el que todas las caras son equiláteras se llama triángulo. correcto.
Propiedades de un tetraedro regular:

• Todos los bordes son iguales.
• Todos los ángulos planos de un tetraedro regular miden 60°.
• Como cada uno de sus vértices es el vértice de tres triángulos regulares, la suma de los ángulos planos en cada vértice es 180°
• Cualquier vértice de un tetraedro regular se proyecta hacia el ortocentro de la cara opuesta (en el punto de intersección de las altitudes del triángulo).

Se nos da un tetraedro regular ABCD con aristas iguales a a. DH es su altura.
Hagamos construcciones adicionales BM - la altura del triángulo ABC y DM - la altura del triángulo ACD.
La altura de BM es igual a BM y es igual a
Considere el triángulo BDM, donde DH, que es la altura del tetraedro, es también la altura de este triángulo.
La altura del triángulo caído al lado MB se puede encontrar usando la fórmula

, Dónde
BM=, DM=, BD=a,
p=1/2 (BM+BD+DM)=
Sustituyamos estos valores en la fórmula de la altura. Obtenemos


Saquemos 1/2a. Obtenemos

Apliquemos la fórmula de diferencia de cuadrados.

Después de pequeñas transformaciones obtenemos


El volumen de cualquier tetraedro se puede calcular mediante la fórmula
,
Dónde ,

Sustituyendo estos valores obtenemos

Por tanto, la fórmula del volumen de un tetraedro regular es

Dónde a–borde del tetraedro

Calcular el volumen de un tetraedro si se conocen las coordenadas de sus vértices

Damos las coordenadas de los vértices del tetraedro.

Del vértice dibujamos los vectores , , .
Para encontrar las coordenadas de cada uno de estos vectores, reste la coordenada inicial correspondiente de la coordenada final. Obtenemos

TRANSCRIPCIÓN DE TEXTO DE LA LECCIÓN:

Buenas tardes Seguimos estudiando el tema: “Paralelismo de rectas y planos”.

Creo que ya está claro que hoy hablaremos de poliedros: las superficies de cuerpos geométricos formados por polígonos.

Es decir, sobre el tetraedro.

Estudiaremos poliedros según plan:

1. definición de tetraedro

2. elementos del tetraedro

3. desarrollo de un tetraedro

4. imagen en un avión

1. construir el triángulo ABC

2. el punto D no se encuentra en el plano de este triángulo

3. Conecta el punto D con segmentos a los vértices del triángulo ABC. Obtenemos los triángulos DAB, DBC y DCA.

Definición: Una superficie formada por cuatro triángulos ABC, DAB, DBC y DCA se llama tetraedro.

Designación: DABC.

Elementos de un tetraedro

Los triángulos que forman un tetraedro se llaman caras, sus lados son aristas y sus vértices se llaman vértices del tetraedro.

¿Cuántas caras, aristas y vértices tiene un tetraedro?

Un tetraedro tiene cuatro caras, seis aristas y cuatro vértices.

Dos aristas de un tetraedro que no tienen vértices comunes se llaman opuestas.

En la figura, los bordes AD y BC, BD y AC, CD y AB son opuestos.

A veces una de las caras de un tetraedro se aísla y se llama base, y las otras tres se llaman caras laterales.

Desarrollo de un tetraedro.

Para hacer un tetraedro a partir de papel necesitarás el siguiente desarrollo:

hay que transferirlo a papel grueso, recortarlo, doblarlo por las líneas de puntos y pegarlo.

En un plano, se representa un tetraedro.

En forma de cuadrilátero convexo o no convexo con diagonales. En este caso, los bordes invisibles se representan con líneas discontinuas.

En la primera imagen, AC es un borde invisible,

en el segundo: EK, LK y KF.

Resolvamos varios problemas típicos de tetraedros:

Encuentra el área de desarrollo de un tetraedro regular con una arista de 5 cm.

Solución. Dibujemos el desarrollo de un tetraedro.

(aparece un escaneo de tetraedro en la pantalla)

Este tetraedro consta de cuatro triángulos equiláteros, por tanto, el área de desarrollo de un tetraedro regular es igual al área de la superficie total del tetraedro o al área de cuatro triángulos regulares.

Encontramos el área de un triángulo regular usando la fórmula:

Luego obtenemos el área del tetraedro igual a:

Sustituyamos la longitud del borde a = 5 cm en la fórmula,

resulta

Respuesta: Área de desarrollo de un tetraedro regular.

Construya una sección del tetraedro con un plano que pase por los puntos M, N y K.

a) En efecto, conectemos los puntos M y N (pertenecientes a la cara ADC), los puntos M y K (pertenecientes a la cara ADB), los puntos N y K (caras DBC). La sección transversal del tetraedro es el triángulo MKN.

b) Conecte los puntos M y K (pertenecen a las caras ADB), los puntos K y N (pertenecen a las caras DCB), luego continúe las líneas MK y AB hasta que se crucen y coloquen el punto P. La línea PN y el punto T se encuentran en el mismo plano ABC y ahora podemos construir la intersección de la recta MK con cada cara. El resultado es un cuadrilátero MKNT, que es la sección deseada.

Todas sus caras son triángulos iguales. El desarrollo de un tetraedro isoédrico es un triángulo dividido por tres líneas medias en cuatro triángulos iguales. En un tetraedro isoédrico, las bases de las alturas, los puntos medios de las alturas y los puntos de intersección de las alturas de las caras se encuentran en la superficie de una esfera (una esfera de 12 puntos) (un análogo del círculo de Euler para un triángulo ).

Propiedades de un tetraedro isoédrico:

• Todas sus caras son iguales (congruentes).
• Los bordes transversales son iguales en pares.
• Los ángulos triédricos son iguales.
• Los ángulos diédricos opuestos son iguales.
• Dos ángulos planos que descansan sobre el mismo borde son iguales.
• La suma de los ángulos planos en cada vértice es 180°.
• El desarrollo de un tetraedro es un triángulo o paralelogramo.
• El paralelepípedo descrito es rectangular.
• El tetraedro tiene tres ejes de simetría.
• Las perpendiculares comunes de los bordes que se cruzan son perpendiculares en pares.
• Las líneas medias son perpendiculares en pares.
• Los perímetros de las caras son iguales.
• Las áreas de las caras son iguales.
• Las alturas del tetraedro son iguales.
• Los segmentos que conectan los vértices con los centros de gravedad de caras opuestas son iguales.
• Los radios de los círculos circunscritos a las caras son iguales.
• El centro de gravedad del tetraedro coincide con el centro de la esfera circunscrita.
• El centro de gravedad coincide con el centro de la esfera inscrita.
• El centro de la esfera circunscrita coincide con el centro de la esfera inscrita.
• La esfera inscrita toca las caras en los centros de los círculos circunscritos alrededor de estas caras.
• La suma de las normales unitarias exteriores (vectores unitarios perpendiculares a las caras) es cero.
• La suma de todos los ángulos diédricos es cero.

tetraedro ortocéntrico

Todas las alturas caídas desde los vértices a las caras opuestas se cruzan en un punto.

Propiedades de un tetraedro ortocéntrico:

• Las altitudes del tetraedro se cruzan en un punto.
• Las bases de las altitudes del tetraedro son los ortocentros de las caras.
• Cada dos aristas opuestas de un tetraedro son perpendiculares.
• Las sumas de los cuadrados de las aristas opuestas de un tetraedro son iguales.
• Los segmentos que conectan los puntos medios de las aristas opuestas del tetraedro son iguales.
• Los productos de los cosenos de ángulos diédricos opuestos son iguales.
• La suma de los cuadrados de las áreas de las caras es cuatro veces menor que la suma de los cuadrados de los productos de aristas opuestas.
• Ud. tetraedro ortocéntrico Los círculos de 9 puntos (círculos de Euler) de cada cara pertenecen a una esfera (esfera de 24 puntos).
• Ud. tetraedro ortocéntrico los centros de gravedad y los puntos de intersección de las alturas de las caras, así como los puntos que dividen los segmentos de cada altura del tetraedro desde el vértice hasta el punto de intersección de las alturas en una proporción de 2: 1, se encuentran en una esfera (esfera de 12 puntos).

tetraedro rectangular

Todos los bordes adyacentes a uno de los vértices son perpendiculares entre sí. Un tetraedro rectangular se obtiene cortando el tetraedro con un plano de un cuboide.

Marco tetraedro

Este es un tetraedro que cumple cualquiera de las siguientes condiciones:

• hay una esfera que toca todos los bordes,
• las sumas de las longitudes de los bordes que se cruzan son iguales,
• las sumas de los ángulos diédricos en bordes opuestos son iguales,
• los círculos inscritos en caras se tocan de dos en dos,
• Se describen todos los cuadriláteros resultantes del desarrollo de un tetraedro.
• Las perpendiculares elevadas a las caras desde los centros de los círculos inscritos en ellas se cruzan en un punto.

Tetraedro proporcional

Propiedades de un tetraedro proporcional:

• Las bi-alturas son iguales. Las bialtitudes de un tetraedro son las perpendiculares comunes a dos de sus aristas que se cruzan (aristas que no tienen vértices comunes).
• Proyección de un tetraedro sobre un plano perpendicular a cualquier bimedianas, hay un rombo. bimedianas Se llama tetraedro a los segmentos que conectan los puntos medios de sus aristas que se cruzan (que no tienen vértices comunes).
• Las caras del paralelepípedo descrito son iguales en tamaño.
• Se mantienen las siguientes relaciones: $4a^2(a\_1)^2-\; (b^2+(b\_1)^2-c^2-(c\_1)^2)^2=4b^2(b\_1)^2-\; (c^2+(c\_1)\; ^2-a^2-(a\_1)^2)^2=4c^2(c\_1)^2-\; (a^2+(a\_1)^2-b^2-(b\_1)^2)^2$, Dónde $a$ Y $a\_1$, $b$ Y $b\_1$, $C$ Y $c\_1$- longitudes de costillas opuestas.
• Para cada par de aristas opuestas de un tetraedro, los planos trazados a través de una de ellas y el centro del segundo son perpendiculares.
• En el paralelepípedo descrito de un tetraedro proporcional se puede inscribir una esfera.

tetraedro incéntrico

En este tipo, los segmentos que conectan los vértices del tetraedro con los centros de círculos inscritos en caras opuestas se cruzan en un punto. Propiedades de un tetraedro incéntrico:

• Los segmentos que conectan los centros de gravedad de las caras del tetraedro con vértices opuestos (medianas del tetraedro) siempre se cruzan en un punto. Este punto es el centro de gravedad del tetraedro.
• Comentario. Si en la última condición reemplazamos los centros de gravedad de las caras con los ortocentros de las caras, entonces se convertirá en una nueva definición. tetraedro ortocéntrico. Si los reemplazamos con los centros de círculos inscritos en las caras, a veces llamados incentros, obtenemos la definición de una nueva clase de tetraedros: incéntrico.
• Los segmentos que conectan los vértices del tetraedro con los centros de círculos inscritos en caras opuestas se cruzan en un punto.
• Las bisectrices de los ángulos de dos caras trazadas hasta el borde común de estas caras tienen una base común.
• Los productos de las longitudes de aristas opuestas son iguales.
• El triángulo formado por los segundos puntos de intersección de tres aristas que emergen de un vértice y cualquier esfera que pase por los tres extremos de estas aristas es equilátero.

tetraedro regular

Este es un tetraedro isoédrico, todas cuyas caras son triángulos regulares. Es uno de los cinco sólidos de Platón.

Propiedades de un tetraedro regular:

• todos los bordes del tetraedro son iguales entre sí,
• todas las caras de un tetraedro son iguales entre sí,
• los perímetros y áreas de todas las caras son iguales.
• Un tetraedro regular es simultáneamente ortocéntrica, de marco, equilátera, incéntrica y proporcional.
• Un tetraedro es regular si pertenece a dos de los siguientes tipos de tetraedros: ortocéntrico, de marco, incéntrico, proporcional, isoédrico.
• Un tetraedro es regular si isoédrico y pertenece a uno de los siguientes tipos de tetraedros: ortocéntrico, de marco, incéntrico, proporcional.
• Un octaedro se puede inscribir en un tetraedro regular; además, cuatro (de ocho) caras del octaedro se combinarán con cuatro caras del tetraedro, los seis vértices del octaedro se combinarán con los centros de seis aristas del tetraedro. .
• Un tetraedro regular consta de un octaedro inscrito (en el centro) y cuatro tetraedros (en los vértices), y los bordes de estos tetraedros y el octaedro son la mitad del tamaño de los bordes del tetraedro regular.
• Un tetraedro regular se puede inscribir en un cubo de dos maneras, con los cuatro vértices del tetraedro alineados con los cuatro vértices del cubo.
• Un tetraedro regular se puede inscribir en un icosaedro; además, los cuatro vértices del tetraedro se combinarán con los cuatro vértices del icosaedro.
• Los bordes que se cruzan en un tetraedro regular son mutuamente perpendiculares.

Volumen de un tetraedro

• El volumen de un tetraedro (teniendo en cuenta el signo), cuyos vértices se encuentran en los puntos $\backslash mathbf(r)\_1\; (x\_1,y\_1,z\_1),$ $\backslash mathbf(r)\_2\; (x\_2,y\_2,z\_2),$ $\backslash mathbf(r)\_3\; (x\_3,y\_3,z\_3),$ $\backslash mathbf(r)\_4\; (x\_4,y\_4,z\_4),$ es igual

$V\; =\; \backslash frac16$

\begin(vmatrix) 1 & x_1 & y_1 & z_1 \\ 1 & x_2 & y_2 & z_2 \\ 1 & x_3 & y_3 & z_3 \\ 1 & x_4 & y_4 & z_4 \end(vmatrix) = \frac16 \begin( vmatrix) x_2 - x_1 & y_2 - y_1& z_2 - z_1\\ x_3 - x_1 & y_3 - y_1& z_3 - z_1\\ x_4 - x_1 & y_4 - y_1& z_4 - z_1 \end(vmatrix), o

$V\; =\; \backslash frac(1)(3)\backslash \; S\; H,$

Dónde $S$ es el área de cualquier cara, y $h$– la altura bajó a esta cara.

• El volumen de un tetraedro en términos de longitudes de aristas se expresa mediante el determinante de Cayley-Menger:

$288\; \backslash cdot\; V^2\; =$

0 y 1 y 1 y 1 y 1 \\ 1 y 0 y d_(12)^2 y d_(13)^2 y d_(14)^2 \\ 1 y d_(12)^2 y 0 y d_( 23)^2 & d_(24)^2 \\ 1 & d_(13)^2 & d_(23)^2 & 0 & d_(34)^2 \\ 1 & d_(14)^2 & d_( 24)^2 y d_(34)^2 y 0

\end(vmatriz).

• Esta fórmula tiene un análogo plano para el área de un triángulo en forma de una variante de la fórmula de Heron mediante un determinante similar.
• Volumen de un tetraedro a lo largo de dos aristas opuestas a Y b, como cruzar líneas que están espaciadas h unos de otros y forman un ángulo entre sí $\backslash fi$, se encuentra mediante la fórmula:

$V\; =\; \backslash frac(1)(6)\; ab\; h\; \backslash sin\; \backslash phi\; .$

$V\; =\; \backslash frac(1)(3)\backslash \; abc\; \backslash sqrt\; (D),$

Dónde $$D=\backslash begin(vmatriz)$$

1 & \cos \gamma & \cos \beta \\ \cos \gamma & 1 & \cos \alpha \\ \cos \beta & \cos \alpha & 1 \end(vmatrix).

• El análogo del plano de la última fórmula es la fórmula para el área de un triángulo en términos de las longitudes de sus dos lados. a Y b, emergiendo de un vértice y formando un ángulo entre sí $\backslash gama$:

$S\; =\; \backslash frac(1)(2)\backslash \; ab\; \backslash sqrt\; (D),$

Dónde $D=\backslash begin(vmatriz)$

1 & \cos \gamma \\ \cos \gamma & 1 \\ \end(vmatrix).

Tetraedros en el microcosmos

• Un tetraedro regular se forma mediante hibridación sp 3 de orbitales atómicos (sus ejes están dirigidos a los vértices del tetraedro regular y el núcleo del átomo central está ubicado en el centro de la esfera descrita del tetraedro regular), por lo que muchos Las moléculas en las que se produce dicha hibridación del átomo central tienen la apariencia de este poliedro.
• Molécula de metano CH 4
• Ión sulfato SO 4 2-, ion fosfato PO 4 3-, ion perclorato ClO 4 - y muchos otros iones
• El diamante C es un tetraedro con una arista igual a 2,5220 angstroms
• Fluorita CaF 2, tetraedro con arista igual a 3, 8626 angstroms
• Esfalerita, ZnS, tetraedro con arista igual a 3,823 angstroms
• Iones complejos - , 2- , 2- , 2+
• Silicatos, cuyas estructuras se basan en el tetraedro de silicio-oxígeno 4-

Tetraedros en la naturaleza

Algunos frutos, cuatro de ellos por un lado, se sitúan en los vértices de un tetraedro casi regular. Este diseño se debe a que los centros de cuatro bolas idénticas que se tocan están ubicados en los vértices de un tetraedro regular. Por lo tanto, los frutos en forma de bolas forman una disposición relativa similar. Por ejemplo, las nueces se pueden disponer de esta forma.

Tetraedros en tecnología

ver también

• Simplex - tetraedro n-dimensional

Escribe una reseña sobre el artículo "Tetraedro"

Notas

Literatura

• Matizen V. E., Dubrovsky. De la geometría del tetraedro “Kvant”, No. 9, 1988 P.66.
• Zaslavsky A. A. // Educación matemática, ser. 3 (2004), núm. 8, págs. 78-92.

Correcto Correcto no convexo Convexo Fórmulas, teoremas, teorías Otro

Extracto que caracteriza al tetraedro.

Al cuarto día, comenzaron los incendios en Zubovsky Val.
Pierre y otras trece personas fueron conducidos a Krymsky Brod, a la cochera de una casa de comerciantes. Mientras caminaba por las calles, Pierre se ahogaba por el humo que parecía cubrir toda la ciudad. Los incendios eran visibles desde diferentes direcciones. Pierre aún no entendía el significado del incendio de Moscú y miraba estos incendios con horror.
Pierre se quedó en la cochera de una casa cerca de Crimea Brod durante cuatro días más, y durante estos días se enteró por la conversación de los soldados franceses que todos los que se encontraban aquí esperaban la decisión del mariscal todos los días. Qué mariscal, Pierre no pudo averiguar por los soldados. Para el soldado, obviamente, el mariscal parecía ser el eslabón de poder más elevado y algo misterioso.
Estos primeros días, hasta el 8 de septiembre, día en que los prisioneros fueron llevados para el segundo interrogatorio, fueron los más difíciles para Pierre.

X
El 8 de septiembre un oficial muy importante entró al granero para ver a los prisioneros, a juzgar por el respeto con que lo trataban los guardias. Este oficial, probablemente un oficial de Estado Mayor, con una lista en la mano, pasó lista a todos los rusos, llamando a Pierre: celui qui n "avoue pas son nom [el que no dice su nombre]. Y, con indiferencia y Mirando perezosamente a todos los prisioneros, ordenó al guardia que era apropiado que el oficial los vistiera y los arreglara antes de llevarlos ante el mariscal. Una hora más tarde llegó una compañía de soldados, y Pierre y otros trece fueron conducidos al Campo de la Doncella. "El día estaba claro, soleado después de la lluvia y el aire estaba inusualmente limpio. El humo no se disipaba como aquel día en que sacaron a Pierre del puesto de vigilancia de Zubovsky Val; el humo se elevaba en columnas en el aire claro. Los incendios No se veían los incendios por ninguna parte, pero columnas de humo se elevaban por todos lados, y todo Moscú, todo lo que Pierre podía ver era un incendio: por todos lados se veían terrenos baldíos con estufas y chimeneas y, a veces, paredes carbonizadas. de casas de piedra. Pierre miraba atentamente los incendios y no reconocía los barrios familiares de la ciudad. En algunos lugares se podían ver iglesias que aún se conservaban. El Kremlin, intacto, se alzaba blanco desde lejos con sus torres e Iván el Grande. Cerca de allí brillaba alegremente la cúpula del convento Novodevichy y desde allí se escuchaba con especial fuerza la campana del Evangelio. Este anuncio recordó a Pierre que era domingo y fiesta de la Natividad de la Virgen María. Pero parecía que no había nadie para celebrar esta festividad: en todas partes había devastación por el incendio, y entre los rusos sólo ocasionalmente había personas andrajosas y asustadas que se escondían al ver a los franceses.
Obviamente, el nido ruso fue devastado y destruido; pero detrás de la destrucción de este orden de vida ruso, Pierre inconscientemente sintió que sobre este nido en ruinas se había establecido su propio orden francés, completamente diferente, pero firme. Lo sintió al ver a aquellos soldados que caminaban alegremente y alegremente, en filas regulares, que lo escoltaban con otros criminales; Lo sintió al ver a un importante funcionario francés en un carruaje doble, conducido por un soldado, que se dirigía hacia él. Lo sintió por los alegres sonidos de la música del regimiento que venía del lado izquierdo del campo, y especialmente lo sintió y lo entendió por la lista que el oficial francés visitante leyó esta mañana, llamando a los prisioneros. Pierre fue llevado por unos soldados, llevado a un lugar u otro con decenas de personas más; parecía que podían olvidarse de él, mezclarlo con otros. Pero no: las respuestas dadas durante el interrogatorio le regresaron en forma de su nombre: celui qui n "avoue pas son nom. Y bajo este nombre, que Pierre temía, ahora lo conducían a alguna parte, con indudable confianza. En sus rostros estaba escrito que todos los demás prisioneros y él eran los que se necesitaban y que los llevaban a donde eran necesarios. Pierre se sintió como una astilla insignificante atrapada en las ruedas de una máquina desconocida para él, pero que funcionaba correctamente.
Pierre y otros criminales fueron conducidos al lado derecho del Campo de la Doncella, no lejos del monasterio, a una gran casa blanca con un enorme jardín. Esta era la casa del príncipe Shcherbatov, en la que Pierre había visitado a menudo al propietario y en la que ahora, como supo por la conversación de los soldados, estaba destinado el mariscal, el duque de Eckmuhl.
Los condujeron al porche y uno a uno los condujeron al interior de la casa. Pierre quedó sexto. A través de una galería acristalada, un vestíbulo y una antecámara que Pierre conocía, lo condujeron a una oficina larga y baja, ante cuya puerta se encontraba un ayudante.
Davout estaba sentado al final de la habitación, encima de la mesa, con gafas en la nariz. Pierre se acercó a él. Davout, sin levantar la vista, aparentemente sostenía un papel que tenía delante. Sin levantar la vista, preguntó en voz baja:
– ¿Qui etes vous? [¿Quién eres?]
Pierre guardó silencio porque no podía pronunciar palabras. Para Pierre, Davout no era sólo un general francés; para Pierre Davout, era un hombre conocido por su crueldad. Al mirar el rostro frío de Davout, quien, como un maestro estricto, accedió a tener paciencia por el momento y esperar una respuesta, Pierre sintió que cada segundo de demora podría costarle la vida; pero no supo qué decir. No se atrevió a decir lo que dijo durante el primer interrogatorio; Revelar el rango y la posición de uno era peligroso y vergonzoso. Pedro guardó silencio. Pero antes de que Pierre pudiera decidir algo, Davout levantó la cabeza, se llevó las gafas a la frente, entrecerró los ojos y miró fijamente a Pierre.
“Conozco a este hombre”, dijo con voz fría y mesurada, obviamente calculada para asustar a Pierre. El frío que antes había bajado por la espalda de Pierre se apoderó de su cabeza como un tornillo de banco.
– Mon general, vous ne pouvez pas me connaitre, je ne vous ai jamais vu... [No podrías conocerme, general, nunca te he visto.]
“C"est un espion russe, [Este es un espía ruso''], lo interrumpió Davout, dirigiéndose a otro general que estaba en la sala y en quien Pierre no había notado. Y Davout se dio la vuelta. Con un inesperado estallido en su voz, Pierre De repente habló rápidamente.
“Non, monseñor”, dijo, recordando de repente que Davout era un duque. - Non, Monseñor, vous n"avez pas pu me connaitre. Je suis un officier militianaire et je n"ai pas quitte Moscú. [No, Su Alteza… No, Su Alteza, no podría conocerme. Soy policía y no he salido de Moscú.]
- ¿Tu nombre? [¿Tu nombre?] - repitió Davout.
- Besouhof. [Bezujov.]
– Qu"est ce qui me prouvera que vous ne mentez pas? [¿Quién me demostrará que no mientes?]
- ¡Monseñor! [¡Su Alteza!] - gritó Pierre con voz no ofendida, pero sí suplicante.
Davout levantó los ojos y miró fijamente a Pierre. Se miraron durante varios segundos y esta mirada salvó a Pierre. Desde este punto de vista, aparte de todas las condiciones de guerra y prueba, se estableció una relación humana entre estas dos personas. Ambos en ese minuto vivieron vagamente innumerables cosas y se dieron cuenta de que ambos eran hijos de la humanidad, que eran hermanos.
A primera vista, para Davout, que apenas levantaba la cabeza de su lista, donde los asuntos humanos y la vida eran llamados números, Pierre era sólo una circunstancia; y, sin tener en cuenta la mala acción en su conciencia, Davout le habría fusilado; pero ahora ya vio una persona en él. Él pensó por un momento.
– Coméntame prouverez vous la verite de ce que vous me dites? [¿Cómo me demostrarás la verdad de tus palabras?] - dijo Davout con frialdad.
Pierre se acordó de Rambal y nombró su regimiento, su apellido y la calle en la que estaba situada la casa.
“Vous n'etes pas ce que vous dites, [No eres lo que dices]”, dijo Davout nuevamente.
Pierre, con voz temblorosa e intermitente, empezó a dar pruebas de la veracidad de su testimonio.
Pero en ese momento entró el ayudante e informó algo a Davout.
Davout de repente sonrió ante la noticia transmitida por el ayudante y comenzó a abotonarse. Al parecer se olvidó por completo de Pierre.
Cuando el ayudante le recordó al prisionero, frunció el ceño, asintió con la cabeza hacia Pierre y le pidió que se lo llevaran. Pero Pierre no sabía dónde debían llevarlo: de regreso a la caseta o al lugar de ejecución preparado, que sus compañeros le mostraron mientras caminaban por el Campo de la Doncella.
Volvió la cabeza y vio que el ayudante volvía a preguntar algo.
- ¡Oui, sin duda! [¡Sí, por supuesto!] - dijo Davout, pero Pierre no sabía qué era "sí".
Pierre no recordaba cómo, cuánto tiempo caminó ni dónde. Él, en un estado de total insensatez y embotamiento, sin ver nada a su alrededor, movió las piernas junto con los demás hasta que todos se detuvieron, y él se detuvo. Durante todo este tiempo, un pensamiento rondaba por la cabeza de Pierre. Era el pensamiento de quién, quién, finalmente lo condenó a muerte. No eran las mismas personas que lo interrogaron en la comisión: ninguno quería y, obviamente, no podía hacerlo. No fue Davout quien lo miró tan humanamente. Un minuto más y Davout se habría dado cuenta de que estaban haciendo algo mal, pero ese momento fue interrumpido por el ayudante que entró. Y este ayudante, obviamente, no quería nada malo, pero tal vez no hubiera entrado. ¿Quién fue finalmente ejecutado, asesinado, quitado la vida? ¿Pierre con todos sus recuerdos, aspiraciones, esperanzas y pensamientos? ¿Quien hizo esto? Y Pierre sintió que no era nadie.
Era una orden, un patrón de circunstancias.
Una especie de orden lo estaba matando, a Pierre, privándolo de la vida, de todo, destruyéndolo.

Desde la casa del príncipe Shcherbatov, los prisioneros fueron conducidos directamente a lo largo del Polo Devichye, a la izquierda del Convento Devichye y conducidos a un huerto en el que había un pilar. Detrás del pilar había un gran hoyo cavado con tierra recién excavada, y una gran multitud de personas formaba un semicírculo alrededor del hoyo y el pilar. La multitud estaba formada por un pequeño número de rusos y un gran número de tropas napoleónicas fuera de formación: alemanes, italianos y franceses con diferentes uniformes. A derecha e izquierda del pilar se encontraban frentes de tropas francesas con uniformes azules con charreteras, botas y shakos rojos.
Los delincuentes fueron colocados en un orden determinado, que estaba en la lista (Pierre estaba sexto), y fueron conducidos a un puesto. De repente sonaron varios tambores de ambos lados, y Pierre sintió que con este sonido era como si le hubieran arrancado parte del alma. Perdió la capacidad de pensar y pensar. Sólo podía ver y oír. Y sólo tenía un deseo: el deseo de que sucediera algo terrible que debía hacerse lo más rápido posible. Pierre miró a sus camaradas y los examinó.
Los dos hombres que estaban en el borde estaban afeitados y vigilados. Uno es alto y delgado; el otro es negro, peludo, musculoso y de nariz chata. El tercero era un criado de la calle, de unos cuarenta y cinco años, de pelo canoso y cuerpo regordete y bien alimentado. El cuarto era un hombre muy apuesto, de espesa barba castaña y ojos negros. El quinto era un obrero de una fábrica, amarillo, delgado, de unos dieciocho años, en bata.
Pierre escuchó que los franceses estaban discutiendo cómo disparar: ¿uno a la vez o dos a la vez? “De dos en dos”, respondió el oficial superior con frialdad y calma. Hubo movimiento en las filas de los soldados, y se notó que todos tenían prisa, y no tenían prisa por hacer algo comprensible para todos, sino como tienen prisa por terminar. una tarea necesaria, pero desagradable e incomprensible.
Un funcionario francés con pañuelo se acercó al lado derecho de la fila de criminales y leyó el veredicto en ruso y francés.
Luego, dos parejas de franceses se acercaron a los delincuentes y, siguiendo las instrucciones del oficial, apresaron a dos guardias que estaban parados en el borde. Los guardias, acercándose al puesto, se detuvieron y, mientras traían las bolsas, miraron en silencio a su alrededor, como un animal herido mira a un cazador adecuado. Uno seguía santiguándose, el otro se rascaba la espalda e hacía un movimiento con los labios como una sonrisa. Los soldados, apresurándose con las manos, empezaron a vendarles los ojos, ponerles bolsas y atarlos a un poste.
Doce fusileros con rifles salieron de detrás de las filas con pasos firmes y medidos y se detuvieron a ocho pasos del poste. Pierre se dio la vuelta para no ver lo que sucedería. De repente se escuchó un estruendo y un rugido que a Pierre le parecieron más fuertes que los truenos más terribles, y miró a su alrededor. Había humo y los franceses, con rostros pálidos y manos temblorosas, estaban haciendo algo cerca del pozo. Trajeron a los otros dos. De la misma manera, con los mismos ojos, estos dos miraban a todos, en vano, sólo con los ojos, en silencio, pidiendo protección y, aparentemente, sin entender ni creer lo que sucedería. No podían creer, porque sólo ellos sabían lo que era su vida para ellos, y por eso no entendían y no creían que se la pudieran quitar.
Pierre quiso no mirar y se volvió; pero de nuevo, como si una terrible explosión golpeara sus oídos, y junto a estos sonidos vio humo, sangre de alguien y los rostros pálidos y asustados de los franceses, que nuevamente hacían algo en el puesto, empujándose unos a otros con manos temblorosas. Pierre, respirando con dificultad, miró a su alrededor, como preguntando: ¿qué es esto? La misma pregunta estaba en todas las miradas que se encontraron con la mirada de Pierre.

En esta lección veremos el tetraedro y sus elementos (arista, superficie, caras, vértices del tetraedro). Y resolveremos varios problemas sobre la construcción de secciones en un tetraedro, utilizando el método general de construcción de secciones.

Tema: Paralelismo de rectas y planos.

Lección: Tetraedro. Problemas al construir secciones en un tetraedro.

¿Cómo construir un tetraedro? Tomemos un triángulo arbitrario. A B C. Cualquier punto D, que no se encuentra en el plano de este triángulo. Obtenemos 4 triángulos. La superficie formada por estos 4 triángulos se llama tetraedro (Fig. 1). Los puntos internos delimitados por esta superficie también forman parte del tetraedro.

Arroz. 1. Tetraedro ABCD

Elementos de un tetraedro
A,B, C, D - vértices de un tetraedro.
AB, C.A., ANUNCIO, ANTES DE CRISTO., BD, CD - aristas del tetraedro.
A B C, ABD, BDC, CAD - caras de tetraedro.

Comentario: se puede tomar plano A B C detrás base de tetraedro y luego señalar D es vértice de un tetraedro. Cada arista del tetraedro es la intersección de dos planos. Por ejemplo, costilla AB- esta es la intersección de planos ABD Y A B C. Cada vértice de un tetraedro es la intersección de tres planos. Vértice A mentiras en aviones A B C, ABD, ADCON. Punto A es la intersección de los tres planos designados. Este hecho se escribe de la siguiente manera: A= A B C ∩ ABD ∩ C.A.D.

Definición de tetraedro

Entonces, tetraedro es una superficie formada por cuatro triángulos.

Borde del tetraedro- la línea de intersección de dos planos del tetraedro.

Haz 4 triángulos iguales a partir de 6 coincidencias. Es imposible solucionar el problema en un avión. Y esto es fácil de hacer en el espacio. Tomemos un tetraedro. 6 coincidencias son sus aristas, cuatro caras del tetraedro y serán cuatro triángulos iguales. El problema esta resuelto.

Dado un tetraedro A B CD. Punto METRO pertenece a una arista del tetraedro AB, punto norte pertenece a una arista del tetraedro END y punto R pertenece al borde DCON(Figura 2.). Construir una sección de un tetraedro con un plano. MNP.

Arroz. 2. Dibujo para el problema 2: construir una sección de un tetraedro con un plano

Solución:
Considere la cara de un tetraedro. DSol. En esta cara del punto norte Y PAG pertenecen a las caras DSol, y por tanto el tetraedro. Pero según la condición del punto. norte, pag pertenecen al plano de corte. Medio, notario público- esta es la línea de intersección de dos planos: el plano de la cara DSol y plano de corte. Supongamos que las líneas rectas notario público Y Sol no paralelo. Se encuentran en el mismo plano. DSol. Encontremos el punto de intersección de las rectas. notario público Y Sol. vamos a denotarlo mi(Fig. 3.).

Arroz. 3. Dibujo para el problema 2. Encontrar el punto E

Punto mi pertenece al plano de sección MNP, ya que se encuentra en la línea notario público, y la línea recta notario público se encuentra completamente en el plano de sección MNP.

también punto mi se encuentra en un avión A B C, porque se encuentra en una línea recta Sol fuera de plano A B C.

lo entendemos COMER- línea de intersección de planos A B C Y MNP, desde puntos mi Y METRO se encuentran simultáneamente en dos planos - A B C Y MNP. Conectemos los puntos METRO Y mi y continúa recto COMER a la intersección con la línea C.A.. Punto de intersección de líneas. COMER Y C.A. vamos a denotar q.

Entonces en este caso NPQМ- la sección requerida.

Arroz. 4. Dibujo del problema 2. Solución del problema 2

Consideremos ahora el caso en el que notario público paralelo ANTES DE CRISTO.. si es heterosexual notario público paralelo a alguna línea, por ejemplo, una línea recta Sol fuera de plano A B C, luego recto notario público paralelo a todo el plano A B C.

El plano de sección deseado pasa por la recta. notario público, paralelo al plano A B C, e interseca el plano en línea recta. MQ. Entonces la línea de intersección MQ paralela a la recta notario público. Obtenemos NPQМ- la sección requerida.

Punto METRO se encuentra de lado ADEN tetraedro A B CD. Construya una sección del tetraedro con un plano que pase por el punto METRO paralelo a la base A B C.

Arroz. 5. Dibujo para el problema 3 Construya una sección de un tetraedro con un plano

Solución:
Plano de corte φ paralelo al plano A B C según la condición, esto significa que este avión φ paralelo a las rectas AB, C.A., Sol.
En plano ABD a través del punto METRO hagamos un directo PQ paralelo AB(Figura 5). Derecho PQ se encuentra en un avión ABD. De manera similar en el avión C.A.D a través del punto R hagamos un directo relaciones públicas paralelo C.A.. tengo un punto R. Dos líneas que se cruzan PQ Y relaciones públicas avión PQR respectivamente paralelo a dos líneas que se cruzan AB Y C.A. avión A B C, que significa aviones A B C Y PQR paralelo. PQR- la sección requerida. El problema esta resuelto.

Dado un tetraedro A B CD. Punto METRO- punto interno, punto en la cara del tetraedro ABD. norte- punto interno del segmento DCON(Figura 6.). Construir el punto de intersección de una línea. NUEVO MÉJICO. y aviones A B C.

Arroz. 6. Dibujo para el problema 4

Solución:
Para solucionar esto construiremos un plano auxiliar. DMinnesota. Déjalo ser recto DMETRO corta a la recta AB en el punto A(Figura 7.). Entonces, SKD- esta es una sección del avión DMinnesota y tetraedro. En plano DMinnesota mentiras y heterosexuales NUEVO MÉJICO., y la línea recta resultante SK. Así que si NUEVO MÉJICO. no paralelo SK, entonces se cruzarán en algún punto R. Punto R y habrá el punto de intersección deseado de la línea. NUEVO MÉJICO. y aviones A B C.

Arroz. 7. Dibujo del problema 4. Solución del problema 4

Dado un tetraedro A B CD. METRO- punto interno de la cara ABD. R- punto interno de la cara A B C. norte- punto interno del borde DCON(Figura 8.). Construya una sección de un tetraedro con un plano que pase por los puntos. METRO, norte Y R.

Arroz. 8. Dibujo para el problema 5 Construya una sección de un tetraedro con un plano

Solución:
Consideremos el primer caso, cuando la línea recta Minnesota no paralelo al plano A B C. En el problema anterior encontramos el punto de intersección de la recta Minnesota y aviones A B C. Este es el punto A, se obtiene utilizando el plano auxiliar DMinnesota, es decir. hacemos DMETRO y obtenemos un punto F. realizamos FQ y en la intersección Minnesota obtenemos un punto A.

Arroz. 9. Dibujo para el problema 5. Encontrar el punto K

hagamos un directo KR. Derecho KR se encuentra tanto en el plano de sección como en el plano A B C. Obteniendo los puntos P 1 Y R 2. Conectando P 1 Y METRO y como continuación entendemos el punto m 1. Conectando el punto R 2 Y norte. Como resultado, obtenemos la sección deseada. Р 1 Р 2 NM 1. El problema en el primer caso está resuelto.
Consideremos el segundo caso, cuando la línea recta Minnesota paralelo al plano A B C. Avión MNP pasa por una linea recta Minnesota paralelo al plano A B C y cruza el avión A B C a lo largo de alguna línea recta R 1 R 2, luego recto R 1 R 2 paralela a la recta dada Minnesota(Figura 10.).

Arroz. 10. Dibujo para el problema 5. La sección requerida.

Ahora dibujemos una línea recta. R 1 M y obtenemos un punto m 1.Р 1 Р 2 NM 1- la sección requerida.

Entonces, observamos el tetraedro y resolvimos algunos problemas típicos del tetraedro. En la próxima lección veremos un paralelepípedo.

1. I. M. Smirnova, V. A. Smirnov. - 5ª edición, corregida y ampliada - M.: Mnemosyne, 2008. - 288 p. : enfermo. Geometría. Grados 10-11: libro de texto para estudiantes de instituciones de educación general (niveles básico y especializado)

2. Sharygin I.F. - M.: Avutarda, 1999. - 208 p.: enfermo. Geometría. Grados 10-11: libro de texto para instituciones de educación general

3. E. V. Potoskuev, L. I. Zvalich. - 6ª edición, estereotipo. - M.: Avutarda, 008. - 233 p. :Illinois. Geometría. Grado 10: Libro de texto para instituciones de educación general con estudio profundo y especializado de matemáticas.

Recursos web adicionales

2. Cómo construir una sección transversal de un tetraedro. Matemáticas ().

3. Festival de ideas pedagógicas ().

Haz problemas en casa sobre el tema “Tetraedro”, cómo encontrar la arista de un tetraedro, las caras de un tetraedro, los vértices y la superficie de un tetraedro.

1. Geometría. Grados 10-11: libro de texto para estudiantes de instituciones de educación general (niveles básico y especializado) I. M. Smirnova, V. A. Smirnov. - 5ª edición, corregida y ampliada - M.: Mnemosyne, 2008. - 288 págs.: ill. Tareas 18, 19, 20 pág.50

2. Punto mi nervadura MAMÁ tetraedro MAVS. Construya una sección del tetraedro con un plano que pase por los puntos. ANTES DE CRISTO Y mi.

3. En el tetraedro MABC, el punto M pertenece a la cara AMV, el punto P pertenece a la cara BMC, el punto K pertenece a la arista AC. Construya una sección del tetraedro con un plano que pase por los puntos. M, R, K.

4. ¿Qué formas se pueden obtener como resultado de la intersección de un tetraedro con un plano?