Практическая работа «Решение систем линейных уравнений третьего порядка методом Крамера. Метод Крамера – теорема, примеры решений Метод крамера примеры с решением 3 порядка

Системой линейных уравнений называется совокупность рассматриваемых совместно нескольких линейных уравнений.

В системе может быть любое число уравнений с любым числом неизвестных.

Решением системы уравнений называется совокупность значений неизвестных, удовлетворяющая всем уравнениям системы, то есть обращающая их в тождества.

Система, имеющая решение, называется совместной, в противном случае – несовместной.

Для решения системы применяют различные методы.

Пусть
(число уравнений равно числу неизвестных).

Метод Крамера

Рассмотрим решение системы трёх линейных уравнений с тремя неизвестными:

(7)

Для нахождения неизвестных
применим формулу Крамера:

(8)

где - определитель системы, элементы которого есть коэффициенты при неизвестных:

.

получается путём замены первого столбца определителя столбцом свободных членов:

.

Аналогично:

;
.

Пример 1. Решить систему по формуле Крамера:

.

Решение: Воспользуемся формулами (8):

;

;

;

;

Ответ:
.

Для любой системы линейных уравнений снеизвестными можно утверждать:

Матричный способ решения

Рассмотрим решение системы (7) трёх линейных уравнений с тремя неизвестными матричным способом.

Используя правила умножения матриц, данную систему уравнений можно записать в виде:
, где

.

Пусть матрица невырожденная, т.е.
. Умножая обе части матричного уравнения слева на матрицу
, обратную матрице, получим:
.

Учитывая, что
, имеем

(9)

Пример 2. Решить систему матричным способом:

.

Решение: Введём матрицы:

- из коэффициентов при неизвестных;

- столбец свободных членов.

Тогда систему можно записать матричным уравнением:
.

Воспользуемся формулой (9). Найдём обратную матрицу
по формуле (6):

;

.

Следовательно,

Получили:

.

Ответ:
.

Метод последовательного исключения неизвестных (метод Гаусса)

Основная идея применяемого метода заключается в последовательном исключении неизвестных. Поясним смысл этого метода на системе трёх уравнений с тремя неизвестными:

.

Допустим, что
(если
, то изменим порядок уравнений, выбрав первым уравнением то, в котором коэффициент прине равен нулю).

Первый шаг: а) делим уравнение
на
; б) умножаем полученное уравнение на
и вычитаем из
; в) затем полученное умножаем на
и вычитаем из
. В результате первого шага будем иметь систему:

,

Второй шаг: поступаем с уравнением
и
точно так же, как с уравнениями
.

В итоге исходная система преобразуется к так называемому ступенчатому виду:

Из преобразованной системы все неизвестные определяются последовательно без труда.

Замечание. Практически удобнее приводить к ступенчатому виду не саму систему уравнений, а матрицу из коэффициентов, при неизвестных, и свободных членов.

Пример 3. Решить методом Гаусса систему:

.

Переход от одной матрицы к другой будем записывать при помощи знака эквивалентности ~.

~
~
~
~

~
.

По полученной матрице выписываем преобразованную систему:

.

Ответ:
.

Замечание: Если система имеет единственное решение, то ступенчатая система приводится к треугольной, то есть к такой, в которой последнее уравнение будет содержать одно неизвестное. В случае неопределённой системы, то есть такой, в которой число неизвестных больше числа линейно независимых уравнений, треугольной системы не будет, так как последнее уравнение будет содержать более одного неизвестного (система имеет бесчисленное множество решений). Когда же система несовместна, то, после приведения её к ступенчатому виду, она будет содержать хотя бы одно значение вида
, то есть уравнение, в котором все неизвестные имеют нулевые коэффициенты, а правая часть отлична от нуля (система решений не имеет). Метод Гаусса применим к произвольной системе линейных уравнений (при любых
и).

Теорема существования решения системы линейных уравнений

При решении системы линейных уравнений методом гаусса ответ на вопрос, совместна или несовместна данная система может быть дан лишь в конце вычислений. Однако часто бывает важно решить вопрос о совместности или несовместности системы уравнений, не находя самих решений. Ответ на этот вопрос даёт следующая теорема Кронекера-Капелли.

Пусть дана система
линейных уравнений снеизвестными:

(10)

Для того, чтобы система (10) была совместной, необходимо и достаточно чтобы ранг матрицы системы

.

был равен рангу её расширенной матрицы

.

Причём, если
, то система (10) имеет единственное решение; если же
, то система имеет бесчисленное множество решений.

Рассмотрим однородную систему (все свободные члены равны нулю) линейных уравнений:

.

Эта система всегда совместна, так как она имеет нулевое решение .

В следующей теореме даны условия, при которых система имеет также решения, отличные от нулевого.

Терема. Для того, чтобы однородная система линейчатых уравнений имела нулевое решение, необходимо и достаточно, чтобы её определитель был равен нулю:

.

Таким образом, если
, то решение- единственное. Если
, то существует бесконечноё множество других ненулевых решений. Укажем один из способов отыскания решений для однородной системы трёх линейных уравнений с тремя неизвестными в случае
.

Можно доказать, что если
, а первое и второе уравнения непропорциональны (линейно независимы), то третье уравнение есть следствие первых двух. Решение однородной системы трёх уравнений с тремя неизвестными сводится к решению двух уравнений с тремя неизвестными. Появляется так называемое свободное неизвестное, которому можно придавать произвольные значения.

Пример 4. Найти все решения системы:

.

Решение. Определитель этой системы

.

Поэтому система имеет нулевые решения. Можно заметить, что первые два уравнения, например, непропорциональны, следовательно, они линейно независимые. Третье является следствием первых двух (получается, если к первому уравнению прибавить удвоенное второе). Отбросив его, получим систему двух уравнений с тремя неизвестными:

.

Полагая, например,
, получим

.

Решая систему двух линейных уравнений, выразим ичерез:
. Следовательно, решение системы можно записать в виде:
, где- произвольное число.

Пример 5. Найти все решения системы:

.

Решение. Нетрудно видеть, что в данной системе только одно независимое уравнение (два других ему пропорциональны). Система из трёх уравнений с тремя неизвестными свелась к одному уравнению с тремя неизвестными. Появляются два свободных неизвестных. Найдя, например, из первого уравнения
при произвольныхи, получим решения данной системы. Общих вид решения можно записать, гдеи- произвольные числа.

Вопросы для самопроверки

Сформулируйте правило Крамера для решения системы линейных уравнений снеизвестными.

В чём сущность матричного способа решения систем?

В чём заключается метод Гаусса решения системы линейных уравнений?

Сформулируйте теорему Кронекера-Капелли.

Сформулируйте необходимое и достаточноё условие существования ненулевых решений однородной системы линейных уравнений.

Примеры для самостоятельного решения

Найдите все решения систем:

1.
; 2.
;

3.
; 4.
;

5.
; 6.
;

7.
; 8.
;

9.
; 10.
;

11.
; 12.
;

13.
; 14.
;

15.
.

Определите, при каких значениях исистема уравнений

а) имеет единственное решение;

б) не имеет решения;

в) имеет бесконечно много решений.

16.
; 17.
;

Найти все решения следующих однородных систем:

18.
; 19.
;

20.
; 21.
;

22.
; 23.
;

Ответы к примерам

1.
; 2.
; 3. Ǿ; 4. Ǿ;

5.
- произвольное число.

6.
, где- произвольное число.

7.
; 8.
; 9. Ǿ; 10. Ǿ;

11.
, где- произвольное число.

12. , гдеи- произвольные числа.

13.
; 14.
гдеи- произвольные числа.

15. Ǿ; 16. а)
; б)
; в)
.

17. а)
; б)
; в)
;

18.
; 19.
; 20., где- произвольное число.

21. , где- произвольное число.

22. , где- произвольное число.

23. , гдеи- произвольные числа.

Для более глубокого понимания происходящего в этой статье можно ознакомиться с .

Рассмотрим однородную систему дифференциальных уравнений третьего порядка

Здесь x(t), y(t), z(t) - искомые функции на промежутке (a, b), a ij (i, j =1, 2, 3) - вещественные числа.

Запишем исходную систему в матричном виде
,
где

Решение исходной системы будем искать в виде
,
где , C 1 , C 2 , C 3 - произвольные постоянные.

Чтобы найти фундаментальную систему решений, нужно решить так называемое характеристическое уравнение

Это уравнение является алгебраическим уравнением третьего порядка, следовательно оно имеет 3 корня. При этом возможны следующие случаи:

1. Корни (собственные значения) действительны и различны.

2. Среди корней (собственных значений) есть комплексно-сопряженные, пусть
- действительный корень
=

3. Корни (собственные значения) действительны. Один из корней кратный.

Чтобы разобраться, как действовать в каждом из этих случаев, нам понадобятся:
Теорема 1.
Пусть - попарно различные собственные значения матрица А, а - соответствующие им собственные векторы. Тогда

образуют фундаментальную систему решений исходной системы.

Замечание .
Пусть - действительное собственное значение матрица А (действительный корень характеристического уравнения), - соответствующий ему собственный вектор.
= - комплексные собственные значения матрицы А, - соответствующий - собственный вектор. Тогда

(Re - действительная часть, Im - мнимая)
образуют фундаментальную систему решений исходной системы. (Т.е. и = рассматриваются вместе)

Теорема 3.
Пусть - корень характеристического уравнения кратности 2. Тогда исходная система имеет 2 линейно независимых решения вида
,
где , - постоянные вектора. Если же кратности 3, то существует 3 линейно независимых решения вида
.
Векторы находятся подствалением решений (*) и (**) в исходную систему.
Чтобы лучше понять метод нахождения решений вида (*) и (**), смотри разобранные типичные примеры ниже.

Теперь рассмотрим более подробно каждый из вышеописанных случаев.

1. Алгоритм решения однородных систем дифференциальных уравнений третьего порядка в случае различных действительных корней характеристического уравнения.
Дана система

1) Составляем характеристическое уравнение

- действительные и различные собственные значения 9корни этого уравнения).
2)Строим , где

3)Строим , где
- собственный вектор матрицы А, соответствующий , т.е. - любое решение системы

4)Строим , где
- собственный вектор матрицы А, соответствующий , т.е. - любое решение системы

5)

составляют фундаментальную систему решений. Далее записываем общее решение исходной системы в виде
,
здесь C 1 , C 2 , C 3 - произвольные постоянные,
,
или в координатном виде

Расмотрим несколько примеров:
Пример 1.




2) Находим


3)Находим


4)Вектор-функции



или в координатной записи

Пример 2.

1)Составляем и решаем характеристическое уравнение:

2) Находим


3)Находим


4)Находим


5)Вектор-функции

образуют фундаментальную систему. Общее решение имеет вид

или в координатной записи

2. Алгоритм решения однородных систем дифференциальных уравнений третьего порядка в случае комплексно-сопряженных корней характеристического уравнения.


- действительный корень,

2)Строим , где

3) Строим

- собственный вектор матрицы А, соответствующий , т.е. удовлетворяет системе

Здесь Re - действительная часть
Im - мнимая часть
4) составляют фундаментальную систему решений. Далее записываем общее решение исходной системы:
, где
С 1 , С 2 ,С 3 произвольные постоянные.

Пример 1.

1) Составляем и решаем характеристическое уравнение

2)Строим

3) Строим
, где

Первое уравнение сократим на 2. Затем ко второму уравнению прибавим первое, умноженное на 2i, а от третьего уравнения отнимем перове, умноженное на 2.

Далее

Следовательно,

4) - фундаментальная система решений. Запишем общее решение исходной системы:

Пример 2.

1) Составляем и решаем харктеристическое уравнение


2)Строим

(т.е. и рассматриваем вместе), где

Второе уравнение умножим на (1-i) и сократим на 2.


Следовательно,

3)
Общее решение исходной системы

или

2. Алгоритм решения однородных систем дифференциальных уравнений третьего порядка в случае кратных корней характеристического уравнения.
Составляем и решаем характеристическое уравнение

Возможны два случая:

Рассмотрим случай а) 1) , где

- собственный вектор матрицы А, соответствующий , т.е удовлетворяет системе

2) Сошлемся на Теорему 3, из которой следует, что существуют два линейно независимых решения вида
,
где , - постоянные векторы. Их возьмем за .
3) - фундаментальная система решений. Далее записываем общее решение исходной системы:

Рассмотрим случай б):
1) Сошлемся на Теорему 3, из которой следует, что существует три линейно независимых решения вида
,
где , , - постоянные векторы. Их возьмем за .
2) - фундаментальная система решений. Далее записываем общее решение исходной системы.

Чтобы лучше понять как находить решения вида (*), рассмотрим несколько типичных примеров.

Пример 1.

Составляем и решаем характеристическое уравнение:

Имеем случай а)
1) Строим
, где

Из второго уравнения вычитаем первое:

? третья строка подобна второй, ее вычеркиваем. Из первого уравнения вычтем второе:

2) = 1 (кратность 2)
Этому корню по Т.3 должно соответствовать два линейно независимых решения вида .
Попробуем найти все линейно незваисимые решения, у которых , т.е. решения вида
.
Такой вектор будет решением тогда и только тогда, когда - собственный вектор, соответствующий =1, т.е.
, или
, вторая и третья строки подобны первой, выкидываем их.

Система свелась к одному уравнению. Следовательно, имеется два свободных неизвестных, например, и . Дадим им сначала значения 1, 0; потом значения 0, 1. Получим такие решения:
.
Следовательно, .
3) - фундаментальная система решений. Осталось записать общее решение исходной системы:
. .. Таким образом существует только одно решение вида Подставим X 3 в эту систему: Вычеркнем третью строку (она подобна второй). Система совместна (имеет решение) при любом с. Пусть с=1.
или

Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.

Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.

Определение . Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).

Определители

получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:

;

.

Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.

Пример 1. Решить систему линейных уравнений:

Согласно теореме Крамера имеем:

Итак, решение системы (2):

онлайн-калькулятором , решающим методом Крамера.

Три случая при решении систем линейных уравнений

Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система совместна и определённа)

Второй случай: система линейных уравнений имеет бесчисленное множество решений

(система совместна и неопределённа)

** ,

т.е. коэффициенты при неизвестных и свободные члены пропорциональны.

Третий случай: система линейных уравнений решений не имеет

(система несовместна)

Итак, система m линейных уравнений с n переменными называется несовместной , если у неё нет ни одного решения, и совместной , если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой , а более одного – неопределённой .

Примеры решения систем линейных уравнений методом Крамера

Пусть дана система

.

На основании теоремы Крамера

………….
,

где
-

определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:

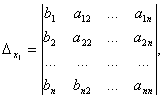
Пример 2.

.

Следовательно, система является определённой. Для нахождения её решения вычисляем определители

По формулам Крамера находим:

Итак, (1; 0; -1) – единственное решение системы.

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.

Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример.

Пример 3. Решить систему линейных уравнений методом Крамера:

.

Решение. Находим определитель системы:

Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных

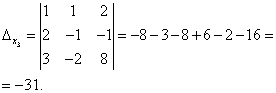
По формулам Крамера находим:

Итак, решение системы - (2; -1; 1).

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.

К началу страницы

Продолжаем решать системы методом Крамера вместе

Как уже говорилось, если определитель системы равен нулю, а определители при неизвестных не равны нулю, система несовместна, то есть решений не имеет. Проиллюстрируем следующим примером.

Пример 6. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных

Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.

В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих переменные, есть ещё и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное. На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов. То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных - буквы. За примерами далеко ходить не надо.

Следующий пример - на аналогичную задачу, только увеличивается количество уравнений, переменных, и букв, обозначающих некоторое действительное число.

Пример 8. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

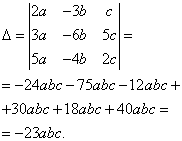
Находим определители при неизвестных

В § 3.3 были показаны ограничения, возникающие при слежении за сигналами изменяющейся частоты при помощи системы второго порядка. Рассмотрим теперь возможность смягчения некоторых из этих ограничений путем введения в систему второго интегратора. Оказывается, что процесс захвата для системы третьего порядка менее устойчив, чем для системы второго порядка, но при помощи второго интегратора можио расширить диапазон слежения за системой, которая в начальный момент была уже захвачена. Передаточная функция фильтра теперь имеет вид

и из (3.1) следует:

После подстановки это выражение приводится к виду

Нормируя и вводя обозначения получим

Обычный метод фазовой плоскости неприменим к дифференциальным уравнениям третьего порядка вследствие того, что в этом случае имеются три начальных условия, соответствующие трем переменным: фазе, частоте и скорости изменения частоты (в механических системах - смещению, скорости и ускорению). В принципе траектории, определяемые уравнением третьего порядка, можно было бы представить в трехмерном пространстве. Всякая же попытка спроектировать эти траектории для J множества начальных условий на плоскость привела бы к столь запутанной диаграмме, что из нее было бы невозможно сделать какие-либо общие заключения.

С другой стороны, если ограничиться одной совокупностью начальных условий, то можно получить проекцию траектории на плоскость . Особое значение представляет следующая совокупность начальных условий: Другими словами, система в начальный момент захвачена, так что ошибки по частоте и фазе равны нулю, когда опорная частота начинает линейно изменяться.

Легко изменить структуру аналоговоговычислительного устройства, чтобы учесть введение второго интегратора.

Рис. 3.19. Проекции траекторий в фазовом пространстве для петли третьего порядка

(см. скан)

На рис. 3.19 изображен ряд траекторий, спроектированных на плоскость . Во всех рассмотренных случаях так что . В гипотетическом трехмерном «фазовом пространстве» траектории начинаются в точке и заканчиваются на оси

На рис. 3.19, а показано поведение системы второго порядка при таких же начальных условиях. Окончательное, или установившееся, значение фазы равно как было показано в § 3.3. Введение второго интегратора приводит к уменьшению установившейся ошибки по фазе до нуля тем быстрее, чем больше При возрастании наибольшая ошибка по фазе также уменьшается, однако за счет уменьшения затухания системы, что приводит к увеличению среднеквадратичной ошибки по фазе (см. рис. 3.19, б - 3.19, ж). Наконец, при система становится неустойчивой.

Получаемое путем увеличения порядка системы улучшение иллюстрируется на рис. 3.20. Здесь как и прежде, но . В § 3.3 было показано, что при такой или большей быстроте линейного изменения частоты система не могла осуществлять слежение. Рис. 3.20, а подтверждает это обстоятельство. С другой стороны, даже при наименьшей степени влияния второго интегратора получается нулевая установившаяся ошибка по фазе. Наибольшее мгновенное значение фазового рассогласования уменьшается при увеличении коэффициента но при система вновь делается неустойчивой.

Аналогичные особенности видны на рис. 3.21-3.23, за исключением того обстоятельства, что при возрастании отношения для поддержания системы в состоянии захвата требуются все возрастающие значения коэффициента В конце концов при приближении отношения к 2 или при необходимо, чтобы было около 1/2. Но из рис. 3.19, ж - 3.23, з видно, что при этом значении система неустойчива. Диапазон значений коэффициента при которых система остается в состоянии захвата в зависимости от отношения представлен на рис. 3.24-3.26 при значениях соответственно. Заштрихована область допустимых значений коэффициента Видно, что при линейном изменении частоты введение системы третьего порядка позволило расширить Диапазон, при котором получается слежение, примерно

Рис. 3.20. Проекции траекторий в фазовом пространстве для петли третьего порядка

(см. скан)

Рис. 3.21. Проекции траекторий в фазовом пространстве для петли третьего порядка

(см. скан)

Рис. 3.22. Проекции траекторий в фазовом пространстве для петли третьего порядка

(см. скан)

Рис. 3.23. Проекции траекторий в фазовом пространстве для петли третьего порядка

(см. скан)

Рис. 3.24. Область состояния захвата системы третьегопорядка

Рис. 3.25. Область состояния захвата системы третьего порядка

Рис. 3.26. Область состояния захвата системы третьего порядка

вдвое больше по сравнению с системой второго порядка при и даже еще большее при меньших значениях

Можно теоретически объяснить колебательный характер изменения коэффициента b при его значениях около или более 1/2. Продифференцировав уравнение (3.41), получим

КОСТРОМСКОЙ ФИЛИАЛ ВОЕННОГО УНИВЕРСИТЕТА РХБ ЗАЩИТЫ

Кафедра «Автоматизации управления войсками»

Только для преподавателей

"Утверждаю"

Начальник кафедры № 9

полковник ЯКОВЛЕВ А.Б.

«____»______________ 2004 г.

доцент А.И.СМИРНОВА

"ОПРЕДЕЛИТЕЛИ.

РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ"

ЛЕКЦИЯ № 2 / 1

Обсуждено на заседании кафедры № 9

«____»___________ 2004г.

Протокол № ___________

Кострома, 2004.

Введение

1. Определители второго и третьего порядка.

2. Свойства определителей. Теорема разложения.

3. Теорема Крамера.

Заключение

Литература

1. В.Е. Шнейдер и др., Краткий курс высшей математики, том I, гл. 2, п.1.

2. В.С. Щипачев, Высшая математика, гл.10, п.2.

ВВЕДЕНИЕ

На лекции рассматриваются определители второго и третьего порядков, их свойства. А также теорема Крамера, позволяющая решать системы линейных уравнений с помощью определителей. Определители используются также в дальнейшем в теме "Векторная алгебра" при вычислении векторного произведения векторов.

1-ый учебный вопросОПРЕДЕЛИТЕЛИ ВТОРОГО И ТРЕТЬЕГО

ПОРЯДКА

Рассмотрим таблицу из четырех чисел вида

Числа в таблице обозначены буквой с двумя индексами. Первый индекс указывает номер строки, второй – номер столбца.

ОПРЕДЕЛЕНИЕ 1. Определителем второго порядка называют выражение вида :

(1)

Числа а 11, …, а 22 называют э л е м е т а м и определителя.

Диагональ, образованная элементами а 11 ; а 22 называется г л а в н ой, а диагональ, образованная элементами а 12 ; а 21 -п о б о ч н ой.

Таким образом, определитель второго порядка равен разности произведений элементов главной и побочной диагоналей.

Заметим, что в ответе получается число.

ПРИМЕРЫ. Вычислить:

Рассмотрим теперь таблицу из девяти чисел, записанных в три строки и три столбца:

ОПРЕДЕЛЕНИЕ 2. Определителем третьего порядка называется выражение вида :

Элементы а 11; а 22 ; а 33 – образуют главную диагональ.

Числа а 13; а 22 ; а 31 – образуют побочную диагональ.

Изобразим, схематически, как образуются слагаемые с плюсом и с минусом:

" + " " – "

С плюсом входят: произведение элементов на главной диагонали, остальные два слагаемых являются произведением элементов, расположенных в вершинах треугольников с основаниями, параллельными главной диагонали.

Слагаемые с минусом образуются по той же схеме относительно побочной диагонали.

Это правило вычисления определителя третьего порядка называют

п р а в и л о м т р е у г о л ь н и к о в.

ПРИМЕРЫ. Вычислить по правилу треугольников:

ЗАМЕЧАНИЕ. Определители называют также д е т е р м и н а н т а м и.

2-ой учебный вопросСВОЙСТВА ОПРЕДЕЛИТЕЛЕЙ.

ТЕОРЕМА РАЗЛОЖЕНИЯ

Свойство 1. Величина определителя не изменится, если его строки поменять местами с соответствующими столбцами.

.

Раскрывая оба определителя, убеждаемся в справедливости равенства.

Свойство 1 устанавливает равноправность строк и столбцов определителя. Поэтому все дальнейшие свойства определителя будем формулировать и для строк и для столбцов.

Свойство 2. При перестановке двух строк (или столбцов) определитель изменяет знак на противоположный, сохраняя абсолютную величину .

.

Свойство 3. Общий множитель элементов строки (или столбца ) можно выносить за знак определителя.

.

Свойство 4. Если определитель имеет две одинаковые строки (или столбца), то он равен нулю.

Это свойство можно доказать непосредственной проверкой, а можно использовать свойство 2.

Обозначим определитель за D. При перестановке двух одинаковых первой и второй строк он не изменится, а по второму свойству он должен поменять знак, т.е.

D = - DÞ 2 D = 0 ÞD = 0.

Свойство 5. Если все элементы какой–то строки (или столбца ) равны нулю, то определитель равен нулю.

Это свойство можно рассматривать как частный случай свойства 3 при

Свойство 6. Если элементы двух строк (или столбцов ) определителя пропорциональны, то определитель равен нулю.

.

Можно доказать непосредственной проверкой или с использованием свойств 3 и 4.

Свойство 7. Величина определителя не изменится, если к элементам какой-либо строки (или столбца) прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и то же число.

.

Доказывается непосредственной проверкой.

Применение указанных свойств может в ряде случаев облегчить процесс вычисления определителей, особенно третьего порядка.

Для дальнейшего нам понадобится понятия минора и алгебраического дополнения. Рассмотрим эти понятия для определения третьего порядка.

ОПРЕДЕЛЕНИЕ 3. Минором данного элемента определителя третьего порядка называется определитель второго порядка, полученный из данного вычеркиванием строки и столбца, на пересечении которых стоит данный элемент.

Минор элемента а i j обозначается М i j . Так для элемента а 11 минор

Он получается, если в определителе третьего порядка вычеркнуть первую строку и первый столбец.

ОПРЕДЕЛЕНИЕ 4. Алгебраическим дополнением элемента определителя называют его минор, умноженный на (-1) k , где k - сумма номеров строки и столбца, на пересечении которых стоит данный элемент.

Алгебраическое дополнение элемента а i j обозначается А i j .

Таким образом, А i j =

.

Выпишем алгебраические дополнения для элементов а 11 и а 12.

. .

Полезно запомнить правило: алгебраическое дополнение элемента определителя равно его минору со знаком плюс , если сумма номеров строки и столбца, в которых стоит элемент, четная, и со знаком минус , если эта сумма нечетная .

ПРИМЕР. Найти миноры и алгебраические дополнения для элементов первой строки определителя:

Ясно, что миноры и алгебраические дополнения могут отличаться только знаком.

Рассмотрим без доказательства важную теорему – теорему разложения определителя.

ТЕОРЕМА РАЗЛОЖЕНИЯ

Определитель равен сумме произведений элементов какой-либо строки или столбца на их алгебраические дополнения.

Используя эту теорему, запишем разложение определителя третьего порядка по первой строке.

.

В развернутом виде:

.

Последнюю формулу можно использовать как основную при вычислении определителя третьего порядка.

Теорема разложения позволяет свести вычисление определителя третьего порядка к вычислению трех определителей второго порядка.

Теорема разложения дает второй способ вычисления определителей третьего порядка.

ПРИМЕРЫ. Вычислить определитель, используя теорему разложения.