वर्ग में x से रूट का व्युत्पन्न। व्युत्पन्न जटिल समारोह। अन्य पृष्ठों पर क्या देखना है

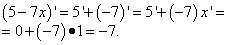
व्युत्पन्न खोजने का संचालन भेदभाव कहा जाता है।

एक तर्क के प्रति दृष्टिकोण की सीमा के रूप में व्युत्पन्न निर्धारित करने के लिए व्युत्पन्न को निर्धारित करने के लिए सबसे सरल (और बहुत सरल) कार्यों को खोजने की समस्याओं को हल करने के परिणामस्वरूप, डेरिवेटिव और सटीक परिभाषित भेदभाव नियमों की एक तालिका दिखाई दी। इसहाक न्यूटन (1643-1727) और गॉटफ्राइड विल्हेल्म लीबनिज़ (1646-1716) पहले डेरिवेटिव्स के निष्कर्षों के क्षेत्र के लिए थे।

इसलिए, हमारे समय में, किसी भी फ़ंक्शन को व्युत्पन्न करने के लिए, तर्क को बढ़ाने के लिए फ़ंक्शन की वृद्धि के अनुपात की उपरोक्त सीमा की गणना करना आवश्यक नहीं है, और आपको केवल डेरिवेटिव और भेदभाव नियमों की तालिका का उपयोग करने की आवश्यकता है । व्युत्पन्न खोजने के लिए, निम्नलिखित एल्गोरिदम उपयुक्त है।

एक व्युत्पन्न खोजने के लिए, स्ट्रोक के संकेत के तहत अभिव्यक्ति के लिए यह आवश्यक है सरल कार्यों के घटकों को अलग करें और निर्धारित करें कि क्या कार्रवाई (काम, राशि, निजी) ये कार्य जुड़े हुए हैं। इसके बाद, प्राथमिक कार्यों के डेरिवेटिव्स डेरिवेटिव्स की तालिका में पाए जाते हैं, और भेदभाव नियमों में डेरिवेटिव्स की मेज और डेरिवेटिव्स, राशियों और निजी के सूत्रों को पाए जाते हैं। पहले दो उदाहरणों के बाद डेरिवेटिव्स और भेदभाव नियमों की तालिका दी जाती है।

उदाहरण 1। एक व्युत्पन्न कार्य खोजें

फेसला। भेदभाव के नियमों से, हम पाते हैं कि कार्यों के कार्य का व्युत्पन्न डेरिवेटिव की राशि है, यानी।

डेरिवेटिव्स की तालिका से, हम पाते हैं कि "आईसीसीए" का व्युत्पन्न एक के बराबर है, और साइनस व्युत्पन्न कोसाइन है। हम इन मूल्यों को डेरिवेटिव की मात्रा में प्रतिस्थापित करते हैं और हमें कार्य व्युत्पन्न की आवश्यक शर्त मिलती है:

उदाहरण 2। एक व्युत्पन्न कार्य खोजें

फेसला। व्युत्पन्न राशि के रूप में अंतर करना जिसमें निरंतर कारक के साथ दूसरा शब्द व्युत्पन्न संकेत से पहुंचा जा सकता है:

यदि अभी तक कोई प्रश्न हैं, जहां से इसे लिया जाता है, वे आमतौर पर टेबल डेरिवेटिव्स और सरलतम भेदभाव नियमों के साथ परिचित होने के बाद स्पष्ट हो जाते हैं। हम अभी उनके पास जाते हैं।

व्युत्पन्न सरल कार्यों की तालिका

1. व्युत्पन्न स्थिर (संख्या)। कोई भी संख्या (1, 2, 5, 200 ...), जो कार्य की अभिव्यक्ति में है। हमेशा शून्य के बराबर। यह याद रखना बहुत महत्वपूर्ण है क्योंकि यह अक्सर आवश्यक है
2. एक स्वतंत्र चर का व्युत्पन्न। अक्सर "iksa"। हमेशा एक के बराबर। लंबे समय तक याद रखना भी महत्वपूर्ण है।
3. व्युत्पन्न डिग्री। उन कार्यों को हल करने में डिग्री आपको अनौपचारिक जड़ों को बदलने की आवश्यकता है।
4. वैरिएबल व्युत्पन्न डिग्री -1 के लिए
5. वर्ग रूट व्युत्पन्न
6. साइनस व्युत्पन्न
7. कोसाइन व्युत्पन्न
8. व्युत्पन्न टेंगेंट
9. कोटैंगेंस का व्युत्पन्न
10. Arksinus व्युत्पन्न
11. Arckosinus व्युत्पन्न
12. आर्कटेनन व्युत्पन्न
13. Arkkotangen व्युत्पन्न
14. व्युत्पन्न प्राकृतिक
15. व्युत्पन्न लघुगणक समारोह
16. प्रदर्शन व्युत्पन्न
17. व्युत्पन्न संकेतक समारोह

भेदभाव नियम

1. व्युत्पन्न राशि या अंतर
2. व्युत्पन्न कार्य
2 ए। अभिव्यक्ति का व्युत्पन्न निरंतर गुणक द्वारा गुणा किया गया
3. निजी व्युत्पन्न
4. व्युत्पन्न जटिल समारोह

नियम 1। अगर कार्य

अलग-अलग किसी बिंदु पर, फिर एक ही बिंदु पर अंतर और कार्य करता है

तथा

वे। बीजगणितीय मात्रा के कार्यों का व्युत्पन्न इन कार्यों के डेरिवेटिव की बीजगणितीय राशि के बराबर है।

कोरोलरी। यदि दो अलग-अलग कार्य स्थायी कार्यकाल पर भिन्न होते हैं, तो उनके डेरिवेटिव बराबर होते हैं।

नियम 2।अगर कार्य

किसी बिंदु पर अलग-अलग, फिर एक ही बिंदु पर अलग-अलग और उनके काम

तथा

वे। दो कार्यों का व्युत्पन्न विभिन्न व्युत्पन्न पर इन कार्यों में से प्रत्येक के कार्यों की मात्रा के बराबर है।

कोरोलरी 1। एक व्युत्पन्न निशान के लिए स्थायी गुणक बनाया जा सकता है:

कोरोलरी 2। कई अलग-अलग कार्यों के काम का व्युत्पन्न अन्य सभी कारकों के व्युत्पन्न के उत्पादों की मात्रा के बराबर है।

उदाहरण के लिए, तीन गुणक के लिए:

नियम 3।अगर कार्य

किसी बिंदु पर अंतर तथा , फिर इस बिंदु पर अलग-अलग और उनके निजीयू / वी, और

वे। निजी दो कार्यों का व्युत्पन्न अंश के बराबर है, जिसका संख्यात्मक संख्यात्मक के व्युत्पन्न और संप्रदाय के व्युत्पन्न पर संख्यात्मक पर संख्यात्मक के उत्पादों में अंतर है, और denominator पिछले संख्यात्मक का वर्ग है ।

अन्य पृष्ठों पर क्या देखना है

वास्तविक कार्यों में काम और निजी के व्युत्पन्न को खोजने के दौरान, कई भिन्नता नियमों को हमेशा लागू किया जा सकता है, इसलिए इन डेरिवेटिव के लिए और अधिक उदाहरण - लेख में"व्युत्पन्न कार्य और निजी कार्य".

टिप्पणी।इसे एक स्थिर (यानी, संख्या) द्वारा राशि में शब्द के रूप में और निरंतर गुणक के रूप में भ्रमित नहीं किया जाना चाहिए! नींव के मामले में, इसका व्युत्पन्न शून्य है, और निरंतर गुणक के मामले में, यह डेरिवेटिव के संकेत के लिए जमा किया जाता है। यह एक सामान्य त्रुटि है जो पर मिलती है आरंभिक चरण डेरिवेटिव का अध्ययन करना, लेकिन कई एकल चरण के उदाहरण पहले ही हल हो चुके हैं, इस त्रुटि का औसत छात्र अब नहीं किया गया है।

और यदि, काम या निजी के भेदभाव के साथ, आपके पास एक शब्द दिखाई दिया है यू"वी , जिसमें यू - एक संख्या, उदाहरण के लिए, 2 या 5, जो एक स्थिर है, इस संख्या का व्युत्पन्न शून्य होगा और इसलिए, संपूर्ण शब्द शून्य होगा (उदाहरण के लिए उदाहरण 10 में अलग हो जाएगा)।

एक और लगातार त्रुटि एक साधारण समारोह के व्युत्पन्न के रूप में एक व्युत्पन्न परिसर समारोह का एक यांत्रिक समाधान है। इसलिये व्युत्पन्न जटिल समारोह समर्पित अलग लेख। लेकिन सबसे पहले हम सरल कार्यों के डेरिवेटिव्स को ढूंढना सीखेंगे।

पाठ्यक्रम में, अभिव्यक्तियों के परिवर्तन के बिना मत करो। ऐसा करने के लिए, आपको नई विंडो में लाभ खोलने की आवश्यकता हो सकती है। डिग्री और जड़ों के साथ कार्रवाई तथा अंशों के साथ कार्रवाई .

यदि आप डिग्री और जड़ों के साथ डेरिवेटिव के समाधान की तलाश में हैं, यानी, जब फ़ंक्शन एक प्रकार की तरह होता है , व्यवसाय का पालन करें "डिग्री और जड़ों के साथ अंशों के व्युत्पन्न" का पालन करें।

यदि आपके पास एक कार्य है , फिर आप "सरल त्रिकोणमितीय कार्यों के डेरिवेटिव" पर हैं।

चरण-दर-चरण उदाहरण - व्युत्पन्न कैसे खोजें

उदाहरण 3। एक व्युत्पन्न कार्य खोजें

फेसला। हम फ़ंक्शन की अभिव्यक्ति का हिस्सा निर्धारित करते हैं: संपूर्ण अभिव्यक्ति कार्य का प्रतिनिधित्व करती है, और इसके कारक रकम हैं, जिनमें से एक में से एक शर्तों में से एक स्थायी गुणक होता है। हम उत्पाद की एक व्युत्पन्न का उपयोग करते हैं: दो कार्यों के काम का एक व्युत्पन्न विभिन्न व्युत्पन्न पर इन कार्यों में से प्रत्येक के कार्यों की मात्रा के बराबर है:

इसके बाद, भेदभाव राशि की मात्रा लागू करें: कार्यों की बीजगणितीय मात्रा का व्युत्पन्न इन कार्यों के डेरिवेटिव की बीजगणितीय राशि के बराबर है। हमारे मामले में, प्रत्येक योग एक शून्य चिह्न के साथ दूसरा शब्द है। प्रत्येक योग में, हम देखते हैं और एक स्वतंत्र चर, जिसका व्युत्पन्न एक के बराबर होता है, और निरंतर (संख्या), जिसका व्युत्पन्न शून्य होता है। तो, "एक्स" हम एक में बदल जाते हैं, और शून्य 5 - शून्य में। दूसरी अभिव्यक्ति में "एक्स" को 2 से गुणा किया जाता है, इसलिए दोनों को "आईकेएसए" के व्युत्पन्न के रूप में एक ही इकाई द्वारा गुणा किया जाता है। हम डेरिवेटिव के निम्नलिखित मान प्राप्त करते हैं:

हम काम की मात्रा में पाए गए डेरिवेटिव्स को प्रतिस्थापित करते हैं और पूरे फ़ंक्शन के व्युत्पन्न की समस्या के लिए आवश्यक शर्त प्राप्त करते हैं:

और आप व्युत्पन्न समस्या के समाधान की जांच कर सकते हैं।

उदाहरण 4। एक व्युत्पन्न कार्य खोजें

फेसला। हमें एक निजी व्युत्पन्न खोजने की जरूरत है। निजी के भेदभाव के लिए सूत्र का उपयोग करना: निजी दो कार्यों का व्युत्पन्न अंश के बराबर है, जिसमें संख्या संख्या संख्यात्मक के व्युत्पन्न और संप्रदाय के व्युत्पन्न पर संख्या और संख्या पर संख्यात्मक के उत्पादों का अंतर है, और डेनोमिनेटर पिछले संख्यात्मक का वर्ग है। हम पाते हैं:

हम पहले से ही उदाहरण 2 में न्यूमर्टल में कारकों का व्युत्पन्न पाए गए हैं। मैं यह भी नहीं भूलूंगा कि वर्तमान उदाहरण में संख्यात्मक में दूसरा कारखाना जो काम एक ऋण चिह्न के साथ लिया जाता है:

यदि आप ऐसे कार्यों के समाधान की तलाश में हैं जिनमें व्युत्पन्न कार्य ढूंढना आवश्यक है, जहां जड़ों और डिग्री की ठोस दौड़, उदाहरण के लिए, , तो व्यवसाय में आपका स्वागत है "डिग्री और जड़ों के साथ अंशों का व्युत्पन्न" .

यदि आपको साइनस डेरिवेटिव, कोसाइन, स्पर्शरेखा और अन्य के बारे में अधिक जानने की आवश्यकता है त्रिकोणमितीय कार्य, यानी, जब फ़ंक्शन कैसा लगता है फिर आप सबक पर हैं "सरल त्रिकोणमितीय कार्यों के डेरिवेटिव्स" .

उदाहरण 5। एक व्युत्पन्न कार्य खोजें

फेसला। इस सुविधा में, हम काम देखते हैं, जिनके कारकों में से एक एक स्वतंत्र चर का एक वर्ग रूट है, जिसके व्युत्पन्न के साथ हमने डेरिवेटिव की मेज पढ़ी है। उत्पाद के व्युत्पन्न और वर्ग रूट व्युत्पन्न के तालिका मूल्य के अनुसार, हमें मिलता है:

व्युत्पन्न पर समस्या का समाधान जांच सकते हैं कैलकुलेटर डेरिवेटिव ऑनलाइन .

उदाहरण 6। एक व्युत्पन्न कार्य खोजें

फेसला। इस सुविधा में, हम निजी देखते हैं, जो एक स्वतंत्र चर से एक वर्ग रूट है। निजी के भेदभाव के शासन के अनुसार, जिसे हमने दोहराया और उदाहरण 4 में लागू किया, हम वर्ग रूट व्युत्पन्न के टैबलेट योग्य मूल्य प्राप्त करते हैं:

अंकक में अंश से छुटकारा पाने के लिए, संख्यात्मक और denominator को गुणा करें।

पावर फ़ंक्शन (एक्स से डिग्री ए) के व्युत्पन्न के लिए सूत्र का आउटपुट। X से जड़ों से डेरिवेटिव माना जाता है। उच्चतम आदेश के व्युत्पन्न का सूत्र। डेरिवेटिव की गणना के उदाहरण।

सामग्री

यह सभी देखें: पावर फ़ंक्शन और जड़ें, सूत्र और अनुसूची
पावर समारोह के ग्राफ

मूल सूत्र

एक्स से डिग्री ए से व्युत्पन्न एक गुणा के बराबर है x से डिग्री एक शून्य से एक:
(1) .

एक्स से डिग्री एम तक डिग्री की डिग्री व्युत्पन्न डिग्री के बराबर है:
(2) .

पावर फ़ंक्शन के व्युत्पन्न के सूत्र का आउटपुट

केस एक्स\u003e 0

विचार करें ऊर्जा समीकरण डिग्री ए के संकेतक के साथ परिवर्तनीय एक्स से:
(3) .
यहाँ एक मनमानी है वास्तविक संख्या। पहले मामले पर विचार करें।

व्युत्पन्न कार्य (3) खोजने के लिए, हम पावर फ़ंक्शन के गुणों का उपयोग करते हैं और हम इसे निम्न फ़ॉर्म में बदलते हैं:
.

अब हम एक व्युत्पन्न पाते हैं, आवेदन करते हैं:
;
.
यहाँ ।

फॉर्मूला (1) साबित हुआ है।

X से डिग्री मीटर तक डिग्री एन की जड़ से उत्पन्न सूत्र का उत्पादन

अब उस फ़ंक्शन पर विचार करें जो निम्न प्रकार की जड़ है:
(4) .

व्युत्पन्न खोजने के लिए, हम रूट को पावर फ़ंक्शन में बदल देते हैं:
.
सूत्र (3) के साथ तुलना में हम देखते हैं
.
फिर
.

सूत्र द्वारा (1) हम एक व्युत्पन्न पाते हैं:
(1) ;
;
(2) .

व्यावहारिक रूप से, फॉर्मूला (2) को याद रखने की कोई आवश्यकता नहीं है। पहले जड़ों को बिजली के कार्यों में परिवर्तित करने के लिए यह अधिक सुविधाजनक है, और उसके बाद फॉर्मूला (1) का उपयोग करके अपने डेरिवेटिव ढूंढें (पृष्ठ के अंत में उदाहरण देखें)।

केस एक्स \u003d 0

यदि, पावर फ़ंक्शन को परिभाषित किया गया है और जब चर का मूल्य x \u003d होता है 0 । एक्स \u003d पर एक व्युत्पन्न कार्य (3) खोजें 0 । ऐसा करने के लिए, हम व्युत्पन्न की परिभाषा का उपयोग करते हैं:
.

स्थानापन्न x \u003d 0 :
.
साथ ही, व्युत्पन्न के तहत, हम सही पक्षीय सीमा को समझते हैं जिसके लिए।

तो, हमने पाया:
.
यह देखा जा सकता है कि जब,।
साथ में ,।
साथ में ,।
यह परिणाम सूत्र (1) के अनुसार दोनों है:
(1) .
इसलिए, फॉर्मूला (1) x \u003d के लिए मान्य है 0 .

केस एक्स।< 0

एक समारोह पर फिर से विचार करें (3):
(3) .
निरंतर ए के कुछ मूल्यों पर, यह निर्धारित किया जाता है और नकारात्मक मान परिवर्ती एक्स। अर्थात्, एक तर्कसंगत संख्या बनने दें। फिर इसे अस्थिर अंश के रूप में दर्शाया जा सकता है:
,
जहां एम और एन पूर्णांक हैं जिनके पास एक सामान्य विभक्त नहीं है।

यदि एन एक अजीब है, तो पावर फ़ंक्शन निर्धारित किया जाता है और परिवर्तनीय एक्स के नकारात्मक मानों के साथ। उदाहरण के लिए, n \u003d के साथ 3 और एम \u003d। 1 अपने पास घन जड़ X से:
.
यह निर्धारित और परिवर्तनीय एक्स के नकारात्मक मानों के तहत निर्धारित है।

पावर फ़ंक्शन (3) के व्युत्पन्न को निरंतर ए के तर्कसंगत मानों के साथ प्राप्त करें, जिसके लिए इसे परिभाषित किया गया है। ऐसा करने के लिए, निम्नलिखित फ़ॉर्म में x की कल्पना करें:
.
फिर
.
हम एक व्युत्पन्न पाते हैं, जो व्युत्पन्न के संकेत के लिए निरंतर बनाते हैं और एक जटिल कार्य के भेदभाव नियम को लागू करते हैं:

.
यहाँ । परंतु
.
चूंकि वह
.
फिर
.
यही है, फॉर्मूला (1) मान्य है और यहां:
(1) .

उच्च आदेशों के व्युत्पन्न

अब हम बिजली समारोह से उच्च आदेश के डेरिवेटिव्स को पाते हैं
(3) .
पहला आदेश व्युत्पन्न हम पहले से ही पाया:
.

व्युत्पन्न के प्रति एक स्थायी प्रतिबिंब बनाकर, हमें एक दूसरा क्रम व्युत्पन्न मिलता है:
.
इसी प्रकार, हम तीसरे और चौथे आदेश के डेरिवेटिव्स को पाते हैं:
;

.

ऐसा लगता है मनमानी nth आदेश का व्युत्पन्न इसमें निम्नलिखित रूप हैं:
.

नोटिस जो अगर ए है प्राकृतिक संख्या ,, तो एन एक व्युत्पन्न है स्थायी है:
.
फिर बाद में डेरिवेटिव शून्य हैं:
,
पर।

डेरिवेटिव की गणना के उदाहरण

उदाहरण

व्युत्पन्न कार्य खोजें:
.

हम जड़ों को डिग्री में बदलते हैं:
;
.
फिर प्रारंभिक कार्य फॉर्म प्राप्त करता है:
.

हमें डिग्री के डेरिवेटिव मिलते हैं:
;
.
निरंतर व्युत्पन्न शून्य है:
.

अनुदेश

रूट व्युत्पन्न खोजने से पहले, हल किए गए उदाहरणों में मौजूद अन्य कार्यों पर ध्यान दें। यदि कार्य में बहुत से अलग-अलग अभिव्यक्तियां हैं, तो वर्ग रूट के व्युत्पन्न के अगले नियम का उपयोग करें:

(√√) "\u003d 1 / 2√x।

और एक घन रूट का व्युत्पन्न खोजने के लिए सूत्र लागू करें:

(³√h) "\u003d 1/3 (³√H) ²,

जहां ³√h के माध्यम से x की घन रूट को चिह्नित किया गया।

यदि भेदभाव के लिए इरादा है, तो फ्रैक्शनल में एक चर पाया जाता है, फिर रूट को संबंधित सूचक के साथ एक पावर फ़ंक्शन में स्थानांतरित करें। एक वर्ग रूट के लिए, यह एक डिग्री ½, और एक घन रूट के लिए होगा - ⅓:

√h \u003d x ^ ½,
³√h \u003d x ^ ⅓,

जहां ^ व्यायाम को संदर्भित करता है।

सभी पर पावर फ़ंक्शन का व्युत्पन्न खोजने के लिए और x ^ ½, x ^, विशेष रूप से, निम्न नियम का उपयोग करें:

(x ^ n) "\u003d n * x ^ (n-1)।

इस अनुपात के मूल व्युत्पन्न के लिए:

(x ^ ½) "\u003d ½ x ^ (-1) और
(x ^ ⅓) "\u003d ⅓ x ^ (-⅔)।

सबकुछ अलग करना, ध्यान से उदाहरण के अन्य भागों को देखें। यदि आपके पास प्रतिक्रिया में बहुत बोझिल अभिव्यक्ति है, तो आप निश्चित रूप से इसे सरल बना सकते हैं। अधिकांश स्कूल उदाहरण डिज़ाइन किया गया ताकि परिणामस्वरूप एक छोटी संख्या या कॉम्पैक्ट अभिव्यक्ति दिखाई दे।

व्युत्पन्न, जड़ों (वर्ग और घन) को खोजने के लिए कई चुनौतियों में अन्य कार्यों के साथ मिलते हैं। इस मामले में रूट व्युत्पन्न खोजने के लिए, निम्नलिखित नियम लागू करें:
व्युत्पन्न स्थिर (निरंतर संख्या, सी) शून्य है: सी "\u003d 0;
एक स्थायी गुणक व्युत्पन्न के संकेत के लिए है: (के * एफ) "\u003d के * (एफ)" (एफ - मनमाने ढंग से कार्य);
कई कार्यों के योग का व्युत्पन्न डेरिवेटिव्स के योग के बराबर है: (एफ + जी) "\u003d (एफ)" + (जी) ";
दो कार्यों के काम का व्युत्पन्न बराबर है ... नहीं, डेरिवेटिव का उत्पाद नहीं, और निम्न अभिव्यक्ति: (एफजी) "\u003d (एफ)" जी + एफ (जी) ";
निजी व्युत्पन्न भी गैर-निजी डेरिवेटिव के बराबर है, लेकिन इसके बाद निम्नलिखित नियम: (एफ / जी) "\u003d (एफ)" जी - एफ (जी) ") / जी²।

ध्यान दें

इस पृष्ठ पर आप विस्तृत कार्य समाधान प्राप्त करने के लिए ऑनलाइन व्युत्पन्न फ़ंक्शन की गणना कर सकते हैं। डेरिवेटिव्स का समाधान उन भेदभाव नियमों का उपयोग करके किया जाता है जो छात्र संस्थान में गणितीय विश्लेषण के दौरान अध्ययन करते हैं। एक व्युत्पन्न फ़ंक्शन खोजने के लिए, आपको डेटा प्रविष्टि नियमों के अनुसार फ़ंक्शन फ़ील्ड में भिन्नता के लिए एक फ़ंक्शन दर्ज करना होगा।

मददगार सलाह

फ़ंक्शन का व्युत्पन्न तर्क की वृद्धि के लिए कार्य की वृद्धि के रिश्ते की सीमा है, जब तर्क की वृद्धि शून्य हो जाती है: इस परिभाषा का गणितीय अर्थ बहुत आसान नहीं है, क्योंकि स्कूल पाठ्यक्रम बीजगणित कार्य की सीमा की अवधारणा या तो बिल्कुल नहीं सीख रही है, या बहुत सतही रूप से अध्ययन किया जाता है। लेकिन विभिन्न कार्यों के डेरिवेटिव्स को कैसे ढूंढना सीखने के लिए, यह आवश्यक नहीं है।

स्रोत:

• एक्स से व्युत्पन्न रूट

1. यादृच्छिक की जड़ के व्युत्पन्न के सूत्र का सामान्य मामला - अंश, जिसमें एक संख्या में, और एक संप्रदाय में, रूट की डिग्री के बराबर संख्या जिसके लिए व्युत्पन्न की गणना की गई थी, जिसे उसी हद तक जड़ से गुणा किया गया था, जिसके आगमन के लिए एक चर है रूट की डिग्री जिसके लिए व्युत्पन्न गणना की गई थी, प्रति यूनिट कम हो गई थी
2. व्युत्पन्न वर्ग रूट - यह पिछले सूत्र का एक विशेष मामला है। एक्स का वर्गम रूट व्युत्पन्न - यह एक अंश है जिसका संख्यात्मक एक के बराबर है, और denominator एक दो बार वर्ग रूट x द्वारा गुणा किया जाता है
3. घन रूट व्युत्पन्नसामान्य सूत्र का एक विशेष मामला भी। एक घन रूट व्युत्पन्न एक इकाई है जो एक्स स्क्वायर से तीन घन रूट में विभाजित है।

नीचे दिए गए परिवर्तन क्या हैं कि व्युत्पन्न और घन रूट के व्युत्पन्न के व्युत्पन्न और घन रूट को खोजने के लिए सूत्रों को आकृति में दिखाया गया है।

बेशक, इन सूत्रों को बिल्कुल याद नहीं किया जा सकता है, अगर हम यह ध्यान में रखते हैं कि व्युत्पन्न डिग्री की जड़ का निष्कर्षण अंश के अंत के समान है, जिसका संप्रदाय एक ही हद तक बराबर है। फिर रूट व्युत्पन्न की नींव संबंधित अंश के व्युत्पन्न को खोजने के लिए सूत्र के उपयोग में कम हो जाती है.

वर्गमूल के तहत व्युत्पन्न चर

(√x) "\u003d 1 / (2√x) या 1/2 x -1/2

व्याख्या:
(√x) "\u003d (x 1/2)"

स्क्वायर रूट 1/2 की प्रदर्शनी के रूप में बिल्कुल वही क्रिया है,इसका मतलब रूट के व्युत्पन्न को खोजने के लिए है, आप एक चर से एक व्युत्पन्न को यादृच्छिक रूप से खोजने के नियम से सूत्र लागू कर सकते हैं:

(x 1/2) "\u003d 1/2 x -1/2 \u003d 1 / (2√x)

घन रूट व्युत्पन्न (तीसरी डिग्री रूट व्युत्पन्न)

क्यूबिक रूट व्युत्पन्न वर्ग के समान सिद्धांत है।

1/3 की डिग्री के रूप में एक घन रूट की कल्पना करें और एक व्युत्पन्न खोजें सामान्य नियम भेदभाव। उपरोक्त तस्वीर में एक संक्षिप्त सूत्र देखा जा सकता है, और स्पष्टीकरण नीचे वर्णित किया गया है कि यह क्यों है।

डिग्री -2/3 1/3 की इकाई के घटाव के परिणामस्वरूप प्राप्त किया जाता है

एक जटिल प्रजातियों के कार्य हमेशा परिभाषा के लिए उपयुक्त नहीं होते हैं। जटिल समारोह। यदि फॉर्म y \u003d sin x का एक फ़ंक्शन है - (2 - 3) · एक आर सी टी जी एक्स एक्स 5 7 x 10 - 17 x 3 + x - 11, इसे y \u003d sin 2 x के विपरीत जटिल नहीं माना जा सकता है।

यह आलेख एक जटिल कार्य और इसकी पहचान की अवधारणा दिखाएगा। हम निष्कर्ष में समाधान के उदाहरणों के साथ एक व्युत्पन्न खोजने के सूत्रों के साथ काम करेंगे। डेरिवेटिव टेबल और भेदभाव नियमों का उपयोग व्युत्पन्न खोजने के लिए समय को कम करता है।

मुख्य परिभाषाएं

परिभाषा 1।

एक जटिल कार्य को ऐसा समारोह माना जाता है जिसमें तर्क भी एक समारोह होता है।

यह इस तरह से संकेत दिया गया है: एफ (जी (एक्स))। हमारे पास यह है कि फ़ंक्शन जी (एक्स) को एक तर्क एफ (जी (एक्स)) माना जाता है।

परिभाषा 2।

यदि कोई फ़ंक्शन एफ है और एक कॉस्टेंटेंट फ़ंक्शन है, तो जी (एक्स) \u003d एलएन एक्स एक प्राकृतिक लॉगरिदम का एक समारोह है। हम यह प्राप्त करते हैं कि जटिल फ़ंक्शन एफ (जी (एक्स)) आर्कट्ज (एलएनएक्स) के रूप में दर्ज किया गया है। या फ़ंक्शन एफ, जो 4 डिग्री में बनाए गए एक समारोह है, जहां जी (एक्स) \u003d x 2 + 2 x - 3 को पूरा माना जाता है तर्कसंगत कार्य, हम इसे एफ (जी (एक्स)) \u003d (x 2 + 2 x - 3) 4 प्राप्त करते हैं।

जाहिर है, जी (एक्स) मुश्किल हो सकता है। उदाहरण y \u003d sin 2 x + 1 x 3-5 से, यह देखा जा सकता है कि मान जी में एक अंश के साथ घन रूट है। इस अभिव्यक्ति को y \u003d f (f 1 (f 2 (x)) के रूप में निरूपित करने की अनुमति है)। जहां हमारे पास यह है कि एफ एक साइनस फ़ंक्शन है, और एफ 1 एक समारोह है वर्गमूल, एफ 2 (एक्स) \u003d 2 एक्स + 1 एक्स 3 - 5 - फ्रैक्शनल तर्कसंगत समारोह।

परिभाषा 3।

घोंसले की डिग्री किसी भी प्राकृतिक संख्या द्वारा निर्धारित की जाती है और इसे वाई \u003d एफ (एफ 1 (एफ 2 (एफ 3 (एफ 3 (एफ 3 (एफ 3 (एफ एन (एक्स)) के रूप में लिखा जाता है))))।

परिभाषा 4।

फ़ंक्शन की अवधारणा संरचना समस्या की स्थिति के तहत नेस्टेड कार्यों की संख्या को संदर्भित करती है। हल करने के लिए, एक व्युत्पन्न जटिल समारोह खोजने के लिए सूत्र का उपयोग करें

(F (g (x))) "\u003d f" (g (x)) · g "(x)

उदाहरण

उदाहरण 1।

फ़ॉर्म y \u003d (2 x + 1) 2 का एक व्युत्पन्न जटिल कार्य खोजें।

फेसला

हालत से, यह देखा जा सकता है कि एफ वर्ग में निर्माण का कार्य है, और जी (एक्स) \u003d 2 एक्स + 1 को एक रैखिक फ़ंक्शन माना जाता है।

हम एक जटिल समारोह के लिए एक व्युत्पन्न सूत्र लागू करते हैं और लिखते हैं:

f "(g (x)) \u003d ((g (x)) 2)" \u003d 2 · (g (x)) 2 - 1 \u003d 2 · g (x) \u003d 2 · (2 \u200b\u200bx + 1); G "(x) \u003d (2 x + 1)" \u003d (2 x) "+ 1" \u003d 2 · x "+ 0 \u003d 2 · 1 · x 1 - 1 \u003d 2 ⇒ (f (g (x))) "\u003d F" (g (x)) · g "(x) \u003d 2 · (2 \u200b\u200bx + 1) · 2 \u003d 8 x + 4

एक सरलीकृत स्रोत प्रकार के कार्य के साथ एक व्युत्पन्न खोजना आवश्यक है। हम पाते हैं:

y \u003d (2 x + 1) 2 \u003d 4 x 2 + 4 x + 1

यहां से हमारे पास यह है

y "\u003d (4 x 2 + 4 x + 1)" \u003d (4 x 2) "+ (4 x)" + 1 "\u003d 4 · (x 2)" + 4 · (x) "+ 0 \u003d 4 · 2 · x 2 - 1 + 4 · 1 · x 1 - 1 \u003d 8 x + 4

परिणाम संयोग।

इस प्रजाति की समस्याओं को हल करते समय, यह समझना महत्वपूर्ण है कि फॉर्म एफ और जी (एक्स) का कार्य कहां स्थित होगा।

उदाहरण 2।

फॉर्म y \u003d sin 2 x और y \u003d sin x 2 के जटिल कार्यों के व्युत्पन्न पाया जाना चाहिए।

फेसला

फ़ंक्शन का पहला फ़ंक्शन सुझाव देता है कि एफ एक वर्ग में निर्माण का एक कार्य है, और जी (एक्स) - साइनस फ़ंक्शन। फिर हमें वह मिलता है

y "\u003d (पाप 2 x)" \u003d 2 · पाप 2 - 1 x · (sin x) "\u003d 2 · पाप x · cos x

दूसरी प्रविष्टि से पता चलता है कि एफ एक साइनस फ़ंक्शन है, और जी (एक्स) \u003d एक्स 2 हम पावर फ़ंक्शन को इंगित करते हैं। यहां से यह इस प्रकार है कि एक जटिल कार्य का उत्पाद के रूप में लिखेंगे

y "\u003d (sin x 2)" \u003d cos (x 2) · (x 2) "\u003d cos (x 2) · 2 · x 2 - 1 \u003d 2 · x · cos (x 2)

व्युत्पन्न वाई \u003d एफ (एफ 1 (एफ 2 (एफ 3 (एफ 3 (एफ 3 (एफएन (एक्स))) के लिए सूत्र))) y "\u003d एफ" (एफ 1 (एफ 2 (एफ 3 (एफ 3 (।) के रूप में दर्ज किया गया है। .. (एफएन (एक्स))))) · एफ 1 "(एफ 2 (एफ 3 (... (एफएन (एक्स)))) · · एफ 2" (एफ 3 (... (एफएन) x)))। । । · F n "(x)

उदाहरण 3।

व्युत्पन्न कार्य y \u003d sin (ln 3 a c t g (2 x)) का पता लगाएं।

फेसला

यह उदाहरण रिकॉर्डिंग की जटिलता और कार्यों के स्थान को निर्धारित करता है। फिर वाई \u003d एफ (एफ 1 (एफ 2 (एफ 3 (एफ 4 (एक्स))))) एफ, एफ 1, एफ 2, एफ 3, एफ 4 (एक्स) द्वारा इंगित करें साइनस, निर्माण का एक कार्य है 3 डिग्री का कार्य, लॉगरिदम और आधार ई के साथ समारोह, आर्केंटेनेंट और रैखिक का कार्य।

जटिल समारोह को निर्धारित करने के लिए सूत्र से, हमारे पास यह है

y "\u003d एफ" (एफ 1 (एफ 2 (एफ 3 (एफ 4 (एक्स)))) · एफ 1 "(एफ 2 (एफ 3 (एफ 4 (एक्स)))) · एफ 2" (एफ 3 (f 4 (x))) · f 3 "(f 4 (x)) · f 4" (x)

हमें मिलता है कि आपको मिलना चाहिए

1. एफ "(एफ 1 (एफ 2 (एफ 3 (एफ 4 (एफ 4 (एफ 4 (एफ 4 (एफ 4 (एक्स))))) डेरिवेटिव्स की मेज पर साइनस के व्युत्पन्न के रूप में, फिर एफ" (एफ 1 (एफ 2 (एफ 3 (एफ 3 (एफ 4 (एक्स)) ))))) \u003d Cos (ln 3 arctg (2 x))।
2. एफ 1 "(एफ 2 (एफ 3 (एफ 4 (एक्स)))) पावर फ़ंक्शन के व्युत्पन्न के रूप में, फिर 1" (एफ 2 (एफ 3 (एफ 4 (एफ 4 (एक्स)))) \u003d 3 · ln 3 - 1 आर्कट्ज (2 x) \u003d 3 · ln 2 arctg (2 x)।
3. एफ 2 "(एफ 3 (एफ 4 (एक्स))) लॉगरिदमिक के व्युत्पन्न के रूप में, फिर एफ 2" (एफ 3 (एफ 4 (एक्स))) \u003d 1 एक आर सी टी जी (2 एक्स)।
4. एफ 3 "(एफ 4 (एक्स)) आर्कटेनेंट के व्युत्पन्न के रूप में, फिर एफ 3" (एफ 4 (एक्स)) \u003d 1 1 + (2 x) 2 \u003d 1 1 + 4 x 2।
5. एक व्युत्पन्न एफ 4 (x) \u003d 2 x ढूंढते समय, सूचक के साथ पावर फ़ंक्शन के व्युत्पन्न के सूत्र का उपयोग करके व्युत्पन्न के संकेत के लिए दबाव चिह्न 2 बनाएं, जो 1 है, तो f 4 "(x) \u003d (2 x) "\u003d 2 · x" \u003d 2 · 1 · x 1 - 1 \u003d 2।

हम मध्यवर्ती परिणामों का एकीकरण उत्पन्न करते हैं और इसे प्राप्त करते हैं

y "\u003d एफ" (एफ 1 (एफ 2 (एफ 3 (एफ 4 (एक्स)))) · एफ 1 "(एफ 2 (एफ 3 (एफ 4 (एक्स)))) · एफ 2" (एफ 3 (f 4 (x))) · f 3 "(f 4 (x)) · f 4" (x) \u003d cos (ln 3 arctg (2 x)) · 3 · ln 2 arctg (2 x) · 1 ARCTG (2 x) · 1 1 + 4 x 2 · 2 \u003d 6 · cos (ln 3 arctg (2 x)) · ln 2 arctg (2 x) arctg (2 x) · (1 + 4 x 2)

ऐसे कार्यों का विश्लेषण एक matryoshki जैसा दिखता है। भिन्नता नियमों को हमेशा एक व्युत्पन्न तालिका का उपयोग करके स्पष्ट रूप से लागू नहीं किया जा सकता है। अक्सर जटिल कार्यों के डेरिवेटिव ढूंढने के लिए सूत्र लागू करना आवश्यक होता है।

जटिल कार्यों से एक जटिल दृश्य में कुछ अंतर हैं। इसे अलग करने की स्पष्ट क्षमता के साथ, डेरिवेटिव ढूंढना विशेष रूप से आसान बना दिया जाएगा।

उदाहरण 4।

ऐसा उदाहरण लाने पर विचार करना आवश्यक है। यदि फ़ॉर्म वाई \u003d टी जी 2 एक्स + 3 टी जी एक्स + 1 का एक फ़ंक्शन है, तो इसे एक जटिल प्रजाति जी (एक्स) \u003d टी जी एक्स, एफ (जी) \u003d जी 2 + 3 जी + 1 के रूप में माना जा सकता है। जाहिर है, एक जटिल व्युत्पन्न के लिए सूत्र का उपयोग आवश्यक है:

f "(g (x)) \u003d (g 2 (x) + 3 g (x) + 1)" \u003d (g 2 (x)) "+ (3 g (x))" + 1 "\u003d \u003d 2 · जी 2 - 1 (एक्स) + 3 · जी "(एक्स) + 0 \u003d 2 जी (एक्स) + 3 · 1 · जी 1 - 1 (एक्स) \u003d 2 जी (एक्स) + 3 \u003d 2 टीजीएक्स + 3; G "(x) \u003d (tgx)" \u003d 1 cos 2 x ⇒ ⇒ y "\u003d (f (g (x)))" \u003d f "(g (x)) · g" (x) \u003d (2 tgx + 3) ) · 1 कॉस 2 एक्स \u003d 2 टीजीएक्स + 3 कॉस 2 एक्स

फॉर्म वाई \u003d टी x 2 + 3 टी जी एक्स + 1 का कार्य जटिल नहीं माना जाता है, क्योंकि इसमें योग टी जी एक्स 2, 3 टी जी एक्स और 1 है। हालांकि, टी जी एक्स 2 को एक जटिल समारोह माना जाता है, हम फॉर्म जी (एक्स) \u003d x 2 और एफ का एक पावर फ़ंक्शन प्राप्त करते हैं, जो स्पर्शरेखा का एक कार्य है। ऐसा करने के लिए, सीधे प्रेषित किया जाना चाहिए। हमें वह मिलता है

वाई "\u003d (टीजीएक्स 2 + 3 टीजीएक्स + 1)" \u003d (टीजीएक्स 2) "+ (3 टीजीएक्स)" + 1 "\u003d \u003d (टीजीएक्स 2)" + 3 · (टीजीएक्स) "+ 0 \u003d (टीजीएक्स 2)" + 3 कॉस 2 एक्स

एक व्युत्पन्न परिसर समारोह (टी जी x 2) खोजने के लिए जाओ:

f "(g (x)) \u003d (tg (g (x)))" \u003d 1 cos 2 g (x) \u003d 1 cos 2 (x 2) g "(x) \u003d (x 2)" \u003d 2 · x 2 - 1 \u003d 2 x ⇒ (tgx 2) "\u003d f" (g (x)) · g "(x) \u003d 2 x cos 2 (x 2)

हम उस वाई "\u003d (टी जी एक्स 2 + 3 टी जी एक्स + 1)" \u003d (टी जी एक्स 2) "+ 3 कॉस 2 एक्स \u003d 2 एक्स कॉस 2 (एक्स 2) + 3 कॉस 2 एक्स

जटिल प्रजातियों के कार्यों को जटिल कार्यों में शामिल किया जा सकता है, और जटिल कार्य स्वयं जटिल प्रजातियों के समग्र कार्य हो सकते हैं।

उदाहरण 5।

उदाहरण के लिए, फॉर्म y \u003d log 3 x 2 + 3 कोस 3 (2 x + 1) + 7 E x 2 + 3 3 + ln 2 x · (x 2 + 1) के जटिल फ़ंक्शन पर विचार करें

इस फ़ंक्शन का प्रतिनिधित्व वाई \u003d एफ (जी (एक्स)) के रूप में किया जा सकता है, जहां मान एफ आधार 3 के आधार पर लॉगरिदम का कार्य है, और जी (एक्स) को फॉर्म एच (एक्स (एक्स) के दो कार्यों का योग माना जाता है ) \u003d x 2 + 3 कॉस 3 (2 x + 1) + 7 EX 2 + 3 3 और K (x) \u003d ln 2 x · (x 2 + 1)। जाहिर है, y \u003d f (h (x) + k (x))।

फ़ंक्शन एच (एक्स) पर विचार करें। यह अनुपात l (x) \u003d x 2 + 3 cos 3 (2 x + 1) + 7 से m (x) \u003d e x 2 + 3 3 है

हमारे पास यह l (x) \u003d x 2 + 3 cos 2 (2 x + 1) + 7 \u003d n (x) + p (x) दो कार्यों का योग है n (x) \u003d x 2 + 7 और p ( एक्स) \u003d 3 कोस 3 (2 एक्स + 1), जहां पी (एक्स) \u003d 3 · पी 1 (पी 2 (पी 3 (एक्स))) एक संख्यात्मक गुणांक 3 के साथ एक जटिल कार्य है, और पी 1 - निर्माण क्यूब, पी 2 कोसाइन फ़ंक्शन, पी 3 (एक्स) \u003d 2 एक्स + 1 - रैखिक फ़ंक्शन में फ़ंक्शन।

यह प्राप्त किया गया था कि एम (एक्स) \u003d EX 2 + 3 3 \u003d q (x) + r (x) दो कार्यों का योग है q (x) \u003d ex 2 और r (x) \u003d 3 3, जहां q (x) ) \u003d क्यू 1 (क्यू 2 (एक्स)) एक जटिल समारोह है, क्यू 1 - एक्सपोनेंट के साथ एक समारोह, क्यू 2 (एक्स) \u003d x 2 - एक पावर फ़ंक्शन।

यह देखा जा सकता है कि एच (x) \u003d l (x) m (x) \u003d n (x) + p (x) q (x) + r (x) \u003d n (x) + 3 · p 1 (p 2) (P 3 (x))) q 1 (q 2 (x)) + r (x)

फॉर्म के (x) \u003d ln 2 x · (x 2 + 1) \u003d s (x) · t (x) की अभिव्यक्ति पर स्विच करते समय, यह देखा जा सकता है कि फ़ंक्शन को जटिल एस (x) \u003d के रूप में दर्शाया गया है एक पूर्णांक तर्कसंगत टी (एक्स) \u003d x 2 + 1 के साथ एलएन 2 एक्स \u003d एस 1 (एस 2 (एक्स)), जहां एस 1 वर्ग में निर्माण का कार्य है, और एस 2 (एक्स) \u003d एलएन एक्स - आधार ई के साथ लघुगणक

यह इस प्रकार है कि अभिव्यक्ति फॉर्म के (एक्स) \u003d एस (एक्स) · टी (एक्स) \u003d एस 1 (एस 2 (एक्स)) · टी (एक्स) ले जाएगी।

फिर हमें वह मिलता है

y \u003d log 3 x 2 + 3 cos 3 (2 x + 1) + 7 EX 2 + 3 3 + ln 2 x · (x 2 + 1) \u003d \u003d fn (x) + 3 · p 1 (p 2 (p) 3 (x))) q 1 (q 2 (x)) \u003d r (x) + s 1 (s 2 (x)) · t (x)

समारोह की संरचनाओं के अनुसार, यह स्पष्ट रूप से बन गया, क्योंकि इसके भेदभाव के दौरान अभिव्यक्ति को सरल बनाने के लिए किस सूत्र का उपयोग किया जाना चाहिए। ऐसे कार्यों को परिचित करने के लिए और उनके समाधान की अवधारणा के लिए, फ़ंक्शन के भेदभाव के कार्य को संदर्भित करना आवश्यक है, यानी, इसे व्युत्पन्न ढूंढना।

यदि आपको पाठ में कोई गलती दिखाई देती है, तो कृपया इसे चुनें और Ctrl + Enter दबाएं