Practical work “Solving systems of linear equations of the third order by the Cramer method. Cramer's method - theorem, examples of solutions Cramer's method examples with 3rd order solution

A system of linear equations is a set of several linear equations considered together.

The system can have any number of equations with any number of unknowns.

The solution of a system of equations is a set of unknown values ​​that satisfies all the equations of the system, that is, converts them into identities.

A system that has a solution is called compatible, otherwise it is called inconsistent.

Various methods are used to solve the system.

Let
(the number of equations is equal to the number of unknowns).

Cramer method

Consider the solution of a system of three linear equations with three unknowns:

(7)

To find the unknown
Let's apply Cramer's formula:

(8)

where - the determinant of the system, the elements of which are the coefficients of the unknowns:

.

obtained by replacing the first column of the determinant column of free members:

.

Similarly:

;
.

Example 1 Solve the system using Cramer's formula:

.

Solution: Let's use formulas (8):

;

;

;

;

Answer:
.

For any system linear equations with unknowns can say:

Matrix solution

Consider the solution of system (7) of three linear equations with three unknowns in a matrix way.

Using the rules of matrix multiplication, this system of equations can be written as:
, where

.

Let the matrix non-degenerate, i.e.
. Multiplying both sides of the matrix equation on the left by the matrix
, the inverse of the matrix , we get:
.

Given that
, we have

(9)

Example 2 Solve the system in a matrix way:

.

Solution: Let's introduce matrices:

- from coefficients at unknown;

- column of free members.

Then the system can be written as a matrix equation:
.

We use formula (9). Let's find the inverse matrix
according to formula (6):

;

.

Consequently,

Got:

.

Answer:
.

Sequential elimination of unknowns (Gauss method)

The main idea of ​​the method used is the successive elimination of unknowns. Let us explain the meaning of this method on a system of three equations with three unknowns:

.

Let's assume that
(if
, then we change the order of the equations, choosing as the first equation the one in which the coefficient at is not equal to zero).

First step: a) divide the equation
on the
; b) multiply the resulting equation by
and subtract from
; c) then multiply the result by
and subtract from
. As a result of the first step, we will have a system:

,

Second step: deal with the equation
and
just like with equations
.

As a result, the original system is transformed to the so-called stepwise form:

From the transformed system, all unknowns are determined sequentially without difficulty.

Comment. In practice, it is more convenient to reduce to a stepped form not the system of equations itself, but a matrix of coefficients, at unknowns, and free terms.

Example 3 Solve the system using the Gaussian method:

.

The transition from one matrix to another will be written using the equivalence sign ~.

~
~
~
~

~
.

Using the resulting matrix, we write out the transformed system:

.

Answer:
.

Note: If the system has a unique solution, then the stepwise system is reduced to a triangular one, that is, to one in which the last equation will contain one unknown. In the case of an indefinite system, that is, one in which the number of unknowns is greater than the number of linearly independent equations, there will be no triangular system, since the last equation will contain more than one unknown (the system has an infinite number of solutions). When the system is inconsistent, then, after reducing it to a stepped form, it will contain at least one kind value
, that is, an equation in which all unknowns have zero coefficients, and the right side is nonzero (there is no solution system). The Gauss method is applicable to an arbitrary system of linear equations (for any
and ).

Existence theorem for a solution to a system of linear equations

When solving a system of linear equations by the Gaussian method, the answer to the question of whether the given system is compatible or inconsistent can be given only at the end of the calculations. However, it is often important to solve the question of the compatibility or inconsistency of a system of equations without finding the solutions themselves. The answer to this question is given by the following Kronecker-Capelli theorem.

Let the system
linear equations with unknown:

(10)

For system (10) to be consistent, it is necessary and sufficient that the rank of the system matrix

.

was equal to the rank of its augmented matrix

.

Moreover, if
, then system (10) has a unique solution; if
, then the system has an infinite number of solutions.

Consider a homogeneous system (all free terms are equal to zero) of linear equations:

.

This system is always consistent since it has a zero solution .

The following theorem gives conditions under which the system also has nonzero solutions.

Terema. In order for a homogeneous system of linear equations to have a zero solution, it is necessary and sufficient that its determinant was equal to zero:

.

Thus, if
, then the solution is unique. If a
, then there are an infinite number of other non-zero solutions. Let us indicate one of the methods for finding solutions for a homogeneous system of three linear equations with three unknowns in the case
.

It can be proved that if
, and the first and second equations are non-proportional (linearly independent), then the third equation is a consequence of the first two. The solution of a homogeneous system of three equations with three unknowns is reduced to the solution of two equations with three unknowns. The so-called free unknown appears, to which arbitrary values ​​can be assigned.

Example 4 Find all system solutions:

.

Solution. The determinant of this system

.

Therefore, the system has zero solutions. It can be seen that the first two equations, for example, are not proportional, hence they are linearly independent. The third is a consequence of the first two (obtained by adding twice the second to the first equation). Rejecting it, we obtain a system of two equations with three unknowns:

.

Assuming, for example,
, we get

.

Solving a system of two linear equations, we express and through :
. Therefore, the solution of the system can be written as:
, where - arbitrary number.

Example 5 Find all system solutions:

.

Solution. It is easy to see that in this system there is only one independent equation (the other two are proportional to it). A system of three equations with three unknowns has been reduced to one equation with three unknowns. Two free unknowns appear. Finding, for example, from the first equation
for arbitrary and , we obtain solutions of this system. The general form of the solution can be written as and - arbitrary numbers.

Questions for self-examination

Formulate Cramer's rule for solving the system linear equations with unknown.

What is the essence of the matrix method for solving systems?

What is the Gauss method for solving a system of linear equations?

Formulate the Kronecker-Capelli theorem.

Formulate a necessary and sufficient condition for the existence of nonzero solutions of a homogeneous system of linear equations.

Examples for self-solving

Find all system solutions:

1.
; 2.
;

3.
; 4.
;

5.
; 6.
;

7.
; 8.
;

9.
; 10.
;

11.
; 12.
;

13.
; 14.
;

15.
.

Determine at what values and system of equations

a) has a unique solution;

b) has no solution;

c) has infinitely many solutions.

16.
; 17.
;

Find all solutions of the following homogeneous systems:

18.
; 19.
;

20.
; 21.
;

22.
; 23.
;

Answers to examples

1.
; 2.
; 3. Ǿ; 4. Ǿ;

5.
- arbitrary number.

6.
, where - arbitrary number.

7.
; 8.
; 9. Ǿ; 10. Ǿ;

11.
, where - arbitrary number.

12. , where and - arbitrary numbers.

13.
; 14.
where and - arbitrary numbers.

15. Ǿ; 16. a)
; b)
; in)
.

17. a)
; b)
; in)
;

18.
; 19.
; 20., where - arbitrary number.

21. , where - arbitrary number.

22. , where - arbitrary number.

23. , where and - arbitrary numbers.

For a deeper understanding of what is happening in this article, you can read.

Consider a homogeneous system of third-order differential equations

Here x(t), y(t), z(t) are the desired functions on the interval (a, b), a ij (i, j =1, 2, 3) are real numbers.

We write the original system in matrix form
,
where

We will seek the solution of the original system in the form
,
where , C 1 , C 2 , C 3 are arbitrary constants.

To find the fundamental system of solutions, it is necessary to solve the so-called characteristic equation

This equation is a third order algebraic equation, so it has 3 roots. In this case, the following cases are possible:

1. Roots (eigenvalues) are real and distinct.

2. Among the roots (eigenvalues) there are complex conjugates, let
- real root
=

3. Roots (eigenvalues) are real. One of the roots is multiple.

To figure out how to act in each of these cases, we need:
Theorem 1.
Let be pairwise distinct eigenvalues ​​of the matrix A, and be the eigenvectors corresponding to them. Then

form a fundamental system of solutions to the original system.

Comment .
Let - the real eigenvalue of the matrix A (the real root of the characteristic equation), - the corresponding eigenvector.
= - complex eigenvalues ​​of the matrix A, - corresponding - eigenvector. Then

(Re - real part, Im - imaginary)
form a fundamental system of solutions to the original system. (i.e. and = are considered together)

Theorem 3.
Let be the root of the characteristic equation of multiplicity 2. Then the original system has 2 linearly independent solutions of the form
,
where , - vector constants. If the multiplicities are 3, then there are 3 linearly independent solutions of the form
.
The vectors are found by substituting solutions (*) and (**) into the original system.
To better understand the method of finding solutions of the form (*) and (**), see the typical examples discussed below.

Now let's take a closer look at each of the above cases.

1. Algorithm for solving homogeneous systems of differential equations of the third order in the case of different real roots of the characteristic equation.
Given system

1) Compose the characteristic equation

are real and distinct eigenvalues ​​(the roots of this equation).
2) We build where

3) We build where
- eigenvector of the matrix A corresponding to , i.e. - any system solution

4) We build where
- eigenvector of the matrix A corresponding to , i.e. - any system solution

5)

constitute the fundamental system of decisions. Next, we write the general solution of the original system in the form
,
here C 1 , C 2 , C 3 are arbitrary constants,
,
or in coordinate form

Let's look at a few examples:
Example 1




2) Find


3) Find


4) Vector functions



or in coordinate notation

Example 2

1) We compose and solve the characteristic equation:

2) Find


3) Find


4) Find


5) Vector functions

form a fundamental system. The general solution has the form

or in coordinate notation

2. Algorithm for solving homogeneous systems of differential equations of the third order in the case of complex conjugate roots of the characteristic equation.


- real root

2) We build where

3) Building

- eigenvector of the matrix A corresponding to , i.e. satisfies the system

Here Re is the real part
Im is the imaginary part
4) constitute the fundamental system of solutions. Next, we write the general solution of the original system:
, where
С 1 , С 2 , С 3 are arbitrary constants.

Example 1

1) We compose and solve the characteristic equation

2) Building

3) Building
, where

We reduce the first equation by 2. Then we add the first equation multiplied by 2i to the second equation, and subtract the pen multiplied by 2 from the third equation.

Further

Consequently,

4) - fundamental system of solutions. We write the general solution of the original system:

Example 2

1) We compose and solve the characteristic equation


2) Building

(i.e., and considered together), where

Multiply the second equation by (1-i) and reduce by 2.


Consequently,

3)
General solution of the original system

or

2. Algorithm for solving homogeneous systems of differential equations of the third order in the case of multiple roots of the characteristic equation.
Compose and solve the characteristic equation

Two cases are possible:

Consider case a) 1) , where

- eigenvector of the matrix A corresponding to , i.e. satisfies the system

2) Let us refer to Theorem 3, from which it follows that there are two linearly independent solutions of the form
,
where , are constant vectors. Let's take them.
3) - fundamental system of solutions. Next, we write the general solution of the original system:

Consider case b):
1) Let us refer to Theorem 3, from which it follows that there are three linearly independent solutions of the form
,
where , , are constant vectors. Let's take them.
2) - fundamental system of solutions. Next, we write down the general solution of the original system.

To better understand how to find solutions of the form (*), consider a few typical examples.

Example 1

We compose and solve the characteristic equation:

We have case a)
1) Building
, where

Subtract the first equation from the second equation:

? The third line is similar to the second, we cross it out. Subtract the second from the first equation:

2) = 1 (multiplicity 2)
According to T.3, this root must correspond to two linearly independent solutions of the form .
Let's try to find all linearly independent solutions for which , i.e. solutions of the form
.
Such a vector will be a solution if and only if is an eigenvector corresponding to =1, i.e.
, or
, the second and third lines are similar to the first, we throw them out.

The system was reduced to one equation. Therefore, there are two free unknowns, for example, and . Let us first give them the values ​​1, 0; then the values ​​0, 1. We get the following solutions:
.
Consequently, .
3) - fundamental system of solutions. It remains to write down the general solution of the original system:
. .. Thus, there is only one solution of the form Substitute X 3 into this system: Cross out the third line (it is similar to the second). The system is consistent (has a solution) for any s. Let c=1.
or

Cramer's method is based on the use of determinants in solving systems of linear equations. This greatly speeds up the solution process.

Cramer's method can be used to solve a system of as many linear equations as there are unknowns in each equation. If the determinant of the system is not equal to zero, then Cramer's method can be used in the solution; if it is equal to zero, then it cannot. In addition, Cramer's method can be used to solve systems of linear equations that have a unique solution.

Definition. The determinant, composed of the coefficients of the unknowns, is called the determinant of the system and is denoted by (delta).

Determinants

are obtained by replacing the coefficients at the corresponding unknowns by free terms:

;

.

Cramer's theorem. If the determinant of the system is nonzero, then the system of linear equations has one single solution, and the unknown is equal to the ratio of the determinants. The denominator contains the determinant of the system, and the numerator contains the determinant obtained from the determinant of the system by replacing the coefficients with the unknown by free terms. This theorem holds for a system of linear equations of any order.

Example 1 Solve the system of linear equations:

According to Cramer's theorem we have:

So, the solution of system (2):

online calculator, Cramer's solution method.

Three cases in solving systems of linear equations

As appears from Cramer's theorems, when solving a system of linear equations, three cases may occur:

First case: the system of linear equations has a unique solution

(the system is consistent and definite)

Second case: the system of linear equations has an infinite number of solutions

(the system is consistent and indeterminate)

** ,

those. the coefficients of the unknowns and the free terms are proportional.

Third case: the system of linear equations has no solutions

(system inconsistent)

So the system m linear equations with n variables is called incompatible if it has no solutions, and joint if it has at least one solution. A joint system of equations that has only one solution is called certain, and more than one uncertain.

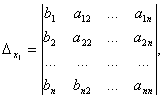
Examples of solving systems of linear equations by the Cramer method

Let the system

.

Based on Cramer's theorem

………….
,

where
-

system identifier. The remaining determinants are obtained by replacing the column with the coefficients of the corresponding variable (unknown) with free members:

Example 2

.

Therefore, the system is definite. To find its solution, we calculate the determinants

By Cramer's formulas we find:

So, (1; 0; -1) is the only solution to the system.

To check the solutions of systems of equations 3 X 3 and 4 X 4, you can use the online calculator, the Cramer solving method.

If there are no variables in the system of linear equations in one or more equations, then in the determinant the elements corresponding to them are equal to zero! This is the next example.

Example 3 Solve the system of linear equations by Cramer's method:

.

Solution. We find the determinant of the system:

Look carefully at the system of equations and at the determinant of the system and repeat the answer to the question in which cases one or more elements of the determinant are equal to zero. So, the determinant is not equal to zero, therefore, the system is definite. To find its solution, we calculate the determinants for the unknowns

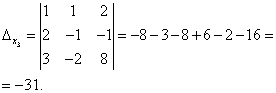
By Cramer's formulas we find:

So, the solution of the system is (2; -1; 1).

To check the solutions of systems of equations 3 X 3 and 4 X 4, you can use the online calculator, the Cramer solving method.

Top of page

We continue to solve systems using the Cramer method together

As already mentioned, if the determinant of the system is equal to zero, and the determinants for the unknowns are not equal to zero, the system is inconsistent, that is, it has no solutions. Let's illustrate with the following example.

Example 6 Solve the system of linear equations by Cramer's method:

Solution. We find the determinant of the system:

The determinant of the system is equal to zero, therefore, the system of linear equations is either inconsistent and definite, or inconsistent, that is, it has no solutions. To clarify, we calculate the determinants for the unknowns

The determinants for the unknowns are not equal to zero, therefore, the system is inconsistent, that is, it has no solutions.

To check the solutions of systems of equations 3 X 3 and 4 X 4, you can use the online calculator, the Cramer solving method.

In problems on systems of linear equations, there are also those where, in addition to the letters denoting variables, there are also other letters. These letters stand for some number, most often a real number. In practice, such equations and systems of equations lead to problems to find the general properties of any phenomena and objects. That is, you invented some new material or device, and to describe its properties, which are common regardless of the size or number of copies, you need to solve a system of linear equations, where instead of some coefficients for variables there are letters. You don't have to look far for examples.

The next example is for a similar problem, only the number of equations, variables, and letters denoting some real number increases.

Example 8 Solve the system of linear equations by Cramer's method:

Solution. We find the determinant of the system:

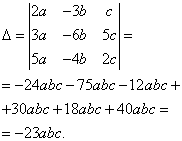
Finding determinants for unknowns

Section 3.3 showed the limitations of tracking signals of varying frequency with a second-order system. Let us now consider the possibility of softening some of these restrictions by introducing a second integrator into the system. It turns out that the capture process for a third-order system is less stable than for a second-order system, but with the help of the second integrator it is possible to expand the tracking range for a system that was already captured at the initial moment. The transfer function of the filter now has the form

and from (3.1) it follows:

After substitution, this expression is reduced to the form

Normalizing and introducing the notation, we obtain

The usual phase plane method is not applicable to third order differential equations due to the fact that in this case there are three initial conditions corresponding to three variables: phase, frequency and rate of change of frequency (in mechanical systems - displacement, speed and acceleration). In principle, the trajectories defined by a third-order equation could be represented in three-dimensional space. Any attempt to project these trajectories for J the set of initial conditions onto the plane would lead to such an intricate diagram that it would be impossible to draw any general conclusions from it.

On the other hand, if we confine ourselves to one set of initial conditions, then we can get the projection of the trajectory onto the plane . Of particular importance is the following set of initial conditions: In other words, the system is initially locked so that the frequency and phase errors are zero when the frequency reference begins to ramp.

It is easy to change the structure of the analog computing device to allow for the introduction of a second integrator.

Rice. 3.19. Projections of trajectories in phase space for a third-order loop

(see scan)

On fig. 3.19 shows a series of trajectories projected onto a plane. In all cases considered, so . In a hypothetical three-dimensional "phase space", trajectories start at a point and end at an axis

On fig. 3.19, a shows the behavior of the second-order system under the same initial conditions. The final, or steady state, value of the phase is the same as shown in § 3.3. The introduction of the second integrator leads to a decrease in the steady-state phase error to zero, the faster, the more When increasing, the largest phase error also decreases, however, due to a decrease in the attenuation of the system, which leads to an increase in the root-mean-square phase error (see Fig. 3.19, b - 3.19, g). Finally, at , the system becomes unstable.

The improvement obtained by increasing the order of the system is illustrated in Fig. 3.20. Here, as before, but . In § 3.3, it was shown that at this or greater rate of frequency ramping, the system could not track. Rice. 3.20, but confirms this circumstance. On the other hand, even with the least degree of influence of the second integrator, a zero steady-state phase error is obtained. The largest instantaneous value of the phase mismatch decreases with increasing coefficient, but at , the system becomes unstable again.

Similar features are seen in Fig. 3.21-3.23, except for the fact that as the ratio increases, ever increasing values ​​of the coefficient are required to maintain the system in a state of capture. In the end, when the ratio approaches 2 or when, it is necessary that it be about 1/2. But from Fig. 3.19, g - 3.23, h it is clear that at this value the system is unstable. The range of values ​​of the coefficient at which the system remains in the state of capture, depending on the ratio, is shown in Fig. 3.24-3.26 at values ​​respectively. The area of ​​permissible values ​​of the coefficient is shaded. It can be seen that with a linear change in frequency, the introduction of a third-order system made it possible to expand the range at which tracking is obtained, approximately

Rice. 3.20. Projections of trajectories in phase space for a third-order loop

(see scan)

Rice. 3.21. Projections of trajectories in phase space for a third-order loop

(see scan)

Rice. 3.22. Projections of trajectories in phase space for a third-order loop

(see scan)

Rice. 3.23. Projections of trajectories in phase space for a third-order loop

(see scan)

Rice. 3.24. The capture state region of a third-order system

Rice. 3.25. The capture state region of a third-order system

Rice. 3.26. The capture state region of a third-order system

twice as much compared to the second-order system at and even more at smaller values

It is possible to theoretically explain the oscillatory nature of the change in the coefficient b at its values ​​of about or more than 1/2. Differentiating equation (3.41), we obtain

KOSTROMA BRANCH OF THE MILITARY UNIVERSITY OF RCHB PROTECTION

Department of "Automation of command and control"

Only for teachers

"I approve"

Head of Department No. 9

Colonel YAKOVLEV A.B.

"____" ______________ 2004

Associate Professor A.I. Smirnova

"DETERMINERS.

SOLUTION OF SYSTEMS OF LINEAR EQUATIONS"

LECTURE № 2 / 1

Discussed at the meeting of the department No. 9

"____" ___________ 2004

Protocol No. ___________

Kostroma, 2004.

Introduction

1. Determinants of the second and third order.

2. Properties of determinants. Decomposition theorem.

3. Cramer's theorem.

Conclusion

Literature

1. V.E. Schneider et al., A Short Course in Higher Mathematics, Volume I, Ch. 2, item 1.

2. V.S. Shchipachev, Higher Mathematics, ch.10, p.2.

INTRODUCTION

The lecture deals with determinants of the second and third orders, their properties. As well as Cramer's theorem, which allows solving systems of linear equations using determinants. Determinants are also used later in the topic "Vector Algebra" when calculating the cross product of vectors.

1st study question QUALIFIERS OF THE SECOND AND THIRD

ORDER

Consider a table of four numbers of the form

The numbers in the table are denoted by a letter with two indices. The first index indicates the row number, the second index indicates the column number.

DEFINITION 1.Second order determinant calledexpressionkind:

(1)

Numbers a 11, …, a 22 are called the elements of the determinant.

Diagonal formed by elements a 11 ; a 22 is called the main, and the diagonal formed by the elements a 12 ; a 21 - on the side.

Thus, the second-order determinant is equal to the difference between the products of the elements of the main and secondary diagonals.

Note that the answer is a number.

EXAMPLES. Calculate:

Consider now a table of nine numbers written in three rows and three columns:

DEFINITION 2. Third order determinant is called an expression of the form:

Elements a 11; a 22 ; a 33 - form the main diagonal.

Numbers a 13; a 22 ; a 31 - form a side diagonal.

Let us depict, schematically, how the terms with plus and minus are formed:

" + " " – "

Plus includes: the product of the elements on the main diagonal, the other two terms are the product of the elements located at the vertices of triangles with bases parallel to the main diagonal.

Terms with a minus are formed in the same way with respect to the secondary diagonal.

This rule for calculating the third order determinant is called

right

EXAMPLES. Calculate by the rule of triangles:

COMMENT. Determinants are also called determinants.

2nd study question PROPERTIES OF DETERMINERS.

EXPANSION THEOREM

Property 1. The value of the determinant will not change if its rows are interchanged with the corresponding columns.

.

Expanding both determinants, we are convinced of the validity of equality.

Property 1 sets the equality of rows and columns of the determinant. Therefore, all further properties of the determinant will be formulated for both rows and columns.

Property 2. When two rows (or columns) are interchanged, the determinant changes sign to the opposite, preserving the absolute value.

.

Property 3. Common multiplier of row elements(or column)can be taken out of the sign of the determinant.

.

Property 4. If the determinant has two identical rows (or columns), then it is equal to zero.

This property can be proved by direct verification, or property 2 can be used.

Denote the determinant by D. When two identical first and second rows are interchanged, it will not change, and by the second property it must change sign, i.e.

D = - DÞ 2 D = 0 ÞD = 0.

Property 5. If all elements of some string(or column)are zero, then the determinant is zero.

This property can be considered as a special case of property 3 with

Property 6. If the elements of two rows(or columns)determinant are proportional, then the determinant is zero.

.

It can be proved by direct verification or by using properties 3 and 4.

Property 7. The value of the determinant does not change if the elements of any row (or column) are added to the corresponding elements of another row (or column), multiplied by the same number.

.

It is proved by direct verification.

The use of these properties can in some cases facilitate the process of calculating determinants, especially of the third order.

For what follows, we need the concepts of minor and algebraic complement. Consider these concepts to define the third order.

DEFINITION 3. Minor of a given element of a third-order determinant is called a second-order determinant obtained from a given one by deleting the row and column at the intersection of which the given element stands.

Element minor aij denoted Mij. So for element a 11 minor

It is obtained by deleting the first row and the first column in the third-order determinant.

DEFINITION 4. Algebraic complement of the determinant element call it a minor multiplied by(-1)k, wherek- the sum of the row and column numbers at the intersection of which the given element is located.

Algebraic element addition aij denoted BUTij.

In this way, BUTij =

.

Let us write out the algebraic complements for the elements a 11 and a 12.

. .

It is useful to remember the rule: the algebraic complement of an element of a determinant is equal to its signed minor a plus, if the sum of the row and column numbers in which the element is located, even, and with sign minus if this amount odd.

EXAMPLE. Find minors and algebraic complements for elements of the first row of the determinant:

It is clear that minors and algebraic complements can differ only in sign.

Let us consider without proof an important theorem - the determinant expansion theorem.

EXPANSION THEOREM

The determinant is equal to the sum of the products of the elements of any row or column and their algebraic complements.

Using this theorem, we write the expansion of the third-order determinant in the first row.

.

Expanded:

.

The last formula can be used as the main one when calculating the third order determinant.

The decomposition theorem allows us to reduce the calculation of the third order determinant to the calculation of three second order determinants.

The decomposition theorem gives a second way to calculate third-order determinants.

EXAMPLES. Calculate the determinant using the decomposition theorem.