अंतरिक्ष में विमान - आवश्यक जानकारी. किसी चित्र में समतल को परिभाषित करने की विधियाँ क्या किसी दिए गए समतल के बाहर बिंदु मौजूद हो सकते हैं?

अंतरिक्ष में डूबी कोई भी ज्यामितीय आकृति अंतरिक्ष में बिंदुओं के एक निश्चित समूह से बनी होती है। एक विमान, ज्यामितीय आकृतियों में से एक के रूप में, कई बिंदुओं का एक संग्रह है। विमान की इस परिभाषा से, अंतरिक्ष में इसकी स्थिति को परिभाषित करने के तरीके स्थापित करना संभव है। ऐसा करने के लिए, संयोजन के सिद्धांत को याद रखना पर्याप्त है - तीन बिंदुओं के माध्यम से जो एक ही रेखा पर नहीं हैं, आप एक विमान खींच सकते हैं, और केवल एक।

चित्र में. 21 अंतरिक्ष में विमान की स्थिति निर्धारित करने के तरीके दिखाता है:

ए - तीन बिंदु जो एक ही रेखा पर नहीं हैं;

बी - एक सीधी रेखा और सीधी रेखा के बाहर लिया गया एक बिंदु;

सी - दो प्रतिच्छेदी सीधी रेखाएँ;

डी - दो समानांतर सीधी रेखाएँ।

एक जटिल चित्र (चित्र 22) में, विमान को निर्दिष्ट किया जा सकता है:

ए - तीन बिंदुओं का प्रक्षेपण जो एक ही रेखा पर नहीं हैं;

बी - एक रेखा और रेखा के बाहर लिए गए एक बिंदु का प्रक्षेपण;

सी - दो प्रतिच्छेदी रेखाओं का प्रक्षेपण;

डी - दो समानांतर रेखाओं का प्रक्षेपण।

उनमें से प्रत्येक चित्र में दिखाया गया है। किसी चित्र में समतल को परिभाषित करने के 22 तरीकों को एक से दूसरे में परिवर्तित किया जा सकता है। इसलिए, उदाहरण के लिए, बिंदु A और B (चित्र 22, a) के माध्यम से एक सीधी रेखा खींचकर, हम चित्र में दिखाए गए समतल असाइनमेंट को प्राप्त करते हैं। 22, बी. इससे आप चित्र में प्रस्तुत विधि पर आगे बढ़ सकते हैं। 22, d, यदि बिंदु C से होकर हम रेखा AB के समानांतर एक रेखा खींचते हैं। यदि बिंदु A, B और C सीधी रेखाओं द्वारा जोड़े में जुड़े हुए हैं, तो हमें त्रिभुज ABC मिलता है - एक सपाट आकृति (चित्र 23), जिसके प्रक्षेपण चित्र में एक विमान को परिभाषित कर सकते हैं।

यह हमेशा याद रखना चाहिए कि विमान, एक ज्यामितीय आकृति के रूप में, असीमित है और इसलिए इसे केवल इस त्रिभुज के क्षेत्र के भीतर निर्माण तक सीमित नहीं किया जा सकता है, क्योंकि सामान्य स्थिति में विमान के प्रक्षेपण प्रत्येक की संपूर्णता पर कब्जा कर लेते हैं। प्रक्षेपण विमान: क्षैतिज पी I, ललाट पी 2 और प्रोफ़ाइल पी 3।

अधिक स्पष्ट रूप से, विमान को सीधी रेखाओं का उपयोग करके परिभाषित किया जा सकता है जिसके साथ यह प्रक्षेपण विमानों को काटता है (चित्र 24, ए)।

इन रेखाओं को समतल के निशान कहा जाता है। सामान्य तौर पर, दोनों पटरियों को प्रक्षेपण अक्ष पर एक बिंदु पर एक दूसरे को काटना चाहिए, जिसे "पटरियों का लुप्त बिंदु" कहा जाता है।

प्रक्षेपण विमानों की दी गई प्रणाली के सापेक्ष विमान की स्थितियों की पूरी विविधता से, उन्हें आमतौर पर तब प्रतिष्ठित किया जाता है जब।

अंतरिक्ष में विमान की स्थिति निर्धारित की जाती है:

• तीन बिंदु जो एक ही रेखा पर नहीं हैं;
• एक सीधी रेखा और सीधी रेखा के बाहर लिया गया एक बिंदु;
• दो प्रतिच्छेदी रेखाएँ;
• दो समानांतर रेखाएँ;
• सपाट आकृति.

इसके अनुसार, विमान को आरेख पर निर्दिष्ट किया जा सकता है:

• तीन बिंदुओं के प्रक्षेपण जो एक ही रेखा पर नहीं हैं (चित्र 3.1, ए);
• एक बिंदु और एक रेखा का प्रक्षेपण (चित्र 3.1,बी);
• दो प्रतिच्छेदी रेखाओं के प्रक्षेपण (चित्र 3.1,सी);
• दो समानांतर रेखाओं के प्रक्षेपण (चित्र 3.1d);
• सपाट आकृति (चित्र 3.1, डी);
• एक विमान के निशान;
• समतल की सबसे बड़ी ढलान की रेखा।

चित्र 3.1 - तलों को परिभाषित करने की विधियाँ

सामान्य विमानएक ऐसा तल है जो किसी भी प्रक्षेपण तल के न तो समानांतर है और न ही लंबवत है।

विमान का पीछा कर रहे हैंप्रक्षेपण विमानों में से किसी एक के साथ दिए गए विमान के प्रतिच्छेदन के परिणामस्वरूप प्राप्त एक सीधी रेखा है।

एक सामान्य विमान में तीन निशान हो सकते हैं: क्षैतिज – απ 1 , ललाट – απ 2 और प्रोफ़ाइल – απ 3, जो ज्ञात प्रक्षेपण विमानों के साथ प्रतिच्छेद करते समय बनता है: क्षैतिज π 1, ललाट π 2 और प्रोफ़ाइल π 3 (चित्र 3.2)।

चित्र 3.2 - एक सामान्य तल के निशान

3.2. आंशिक विमान

आंशिक समतल- प्रक्षेपणों के तल के लंबवत या समानांतर एक तल।

प्रक्षेपण तल के लंबवत तल को प्रक्षेपण कहा जाता है और इस प्रक्षेपण तल पर इसे एक सीधी रेखा के रूप में प्रक्षेपित किया जाएगा।

प्रक्षेपण तल की संपत्ति: प्रक्षेपित तल से संबंधित सभी बिंदुओं, रेखाओं, समतल आकृतियों का प्रक्षेपण तल के झुके हुए निशान पर होता है(चित्र 3.3)।

चित्र 3.3 - सामने से प्रक्षेपित विमान, जिसमें शामिल हैं: बिंदु ए, में, साथ; पंक्तियां एसी, अब, सूरज; त्रिकोण तल एबीसी

सामने प्रक्षेपण विमान – प्रक्षेपणों के ललाट तल के लंबवत् तल(चित्र 3.4, ए)।

क्षैतिज प्रक्षेपण विमान – प्रक्षेपणों के क्षैतिज तल के लंबवत् तल(चित्र 3.4, बी)।

प्रोफाइल-प्रोजेक्टिंग विमान – प्रक्षेपणों के प्रोफ़ाइल तल के लंबवत समतल.

प्रक्षेपण तलों के समान्तर तल कहलाते हैं समतल विमानया डबल प्रक्षेपित विमान.

फ्रंट लेवल प्लेन – प्रक्षेपण के ललाट तल के समानांतर समतल(चित्र 3.4, सी)।

क्षैतिज स्तर का समतल – प्रक्षेपण के क्षैतिज तल के समानांतर समतल(चित्र 3.4, डी)।

स्तर का प्रोफ़ाइल तल – प्रक्षेपण के प्रोफाइल विमान के समानांतर विमान(चित्र 3.4, डी)।

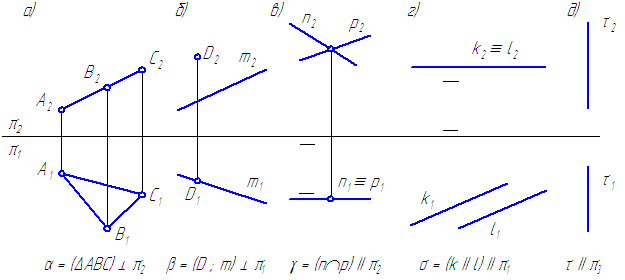
चित्र 3.4 - विशेष स्थिति के विमानों के आरेख

3.3. एक समतल में एक बिंदु और एक सीधी रेखा। एक बिंदु और एक सीधे तल का संबंध

एक बिंदु किसी समतल का होता है यदि वह इस तल में पड़ी किसी रेखा से संबंधित हो(चित्र 3.5)।

एक सीधी रेखा एक समतल की होती है यदि उसमें समतल के साथ कम से कम दो उभयनिष्ठ बिंदु हों(चित्र 3.6)।

चित्र 3.5 - एक बिंदु का एक समतल से संबंध

α = एम // एन

डी∈ एन⇒ डी∈ α

चित्र 3.6 - एक सीधे तल से संबंधित

व्यायाम

एक चतुर्भुज द्वारा परिभाषित एक समतल दिया गया है (चित्र 3.7, ए)। शीर्ष के क्षैतिज प्रक्षेपण को पूरा करना आवश्यक है साथ.

ए	बी

चित्र 3.7 - समस्या समाधान

समाधान :

1. ए बी सी डी- एक समतल चतुर्भुज जो एक तल को परिभाषित करता है।
2. आइए इसमें विकर्ण बनाएं एसी।और बी.डी(चित्र 3.7, बी), जो सीधी रेखाओं को प्रतिच्छेद कर रहे हैं, एक ही तल को परिभाषित भी कर रहे हैं।
3. प्रतिच्छेदी रेखाओं की कसौटी के अनुसार हम इन रेखाओं के प्रतिच्छेद बिंदु का क्षैतिज प्रक्षेपण बनाएंगे - कइसके ज्ञात ललाट प्रक्षेपण के अनुसार: ए 2 सी 2 ∩ बी 2 डी 2 =के 2 .
4. आइए प्रक्षेपण कनेक्शन लाइन को तब तक पुनर्स्थापित करें जब तक कि यह सीधी रेखा के क्षैतिज प्रक्षेपण के साथ प्रतिच्छेद न हो जाए बी.डी: विकर्ण प्रक्षेपण पर बी 1 डी 1 हम निर्माण कर रहे हैं को 1 .
5. के माध्यम से ए 1 को 1 हम एक विकर्ण प्रक्षेपण करते हैं ए 1 साथ 1 .
6. पूर्ण विराम साथ 1 को प्रक्षेपण कनेक्शन लाइन के माध्यम से तब तक प्राप्त किया जाता है जब तक कि यह विस्तारित विकर्ण के क्षैतिज प्रक्षेपण के साथ प्रतिच्छेद न हो जाए ए 1 को 1 .

3.4. मुख्य समतल रेखाएँ

एक समतल में अनंत संख्या में सीधी रेखाएँ बनाई जा सकती हैं, लेकिन समतल में कुछ विशेष सीधी रेखाएँ पड़ी होती हैं, जिन्हें कहा जाता है विमान की मुख्य लाइनें (चित्र 3.8-3.11)।

सीधा स्तर या विमान के समानांतरकिसी दिए गए तल में पड़ी एक सीधी रेखा है और प्रक्षेपण तलों में से एक के समानांतर है।

क्षैतिज या क्षैतिज स्तर रेखा एच(पहला समानांतर) किसी दिए गए तल में पड़ी एक सीधी रेखा है और प्रक्षेपण के क्षैतिज तल के समानांतर है (π 1)(चित्र 3.8, ए; 3.9)।

सामने या सामने का स्तर सीधा एफ(दूसरा समानांतर) किसी दिए गए तल में पड़ी एक सीधी रेखा है और प्रक्षेपण के ललाट तल के समानांतर है (π 2)(चित्र 3.8, बी; 3.10)।

लेवल प्रोफाइल लाइन पी(तीसरा समानांतर) किसी दिए गए तल में पड़ी एक सीधी रेखा है और प्रक्षेपण के प्रोफ़ाइल तल के समानांतर है (π 3)(चित्र 3.8, सी; 3.11)।

चित्र 3.8 ए - त्रिभुज द्वारा परिभाषित तल में स्तर की क्षैतिज सीधी रेखा

चित्र 3.8 बी - त्रिभुज द्वारा परिभाषित तल में स्तर की ललाट सीधी रेखा

चित्र 3.8 सी - त्रिभुज द्वारा परिभाषित तल में स्तर प्रोफ़ाइल रेखा

चित्र 3.9 - पटरियों द्वारा परिभाषित समतल में स्तर की क्षैतिज सीधी रेखा

चित्र 3.10 - पटरियों द्वारा परिभाषित समतल में स्तर की ललाट सीधी रेखा

चित्र 3.11 - पटरियों द्वारा परिभाषित समतल में लेवल प्रोफाइल लाइन

3.5. सीधी रेखा और तल की पारस्परिक स्थिति

किसी दिए गए तल के संबंध में एक सीधी रेखा समानांतर हो सकती है और उसके साथ एक उभयनिष्ठ बिंदु हो सकता है, अर्थात प्रतिच्छेद कर सकता है।

3.5.1. एक सीधे विमान की समानता

एक सीधे तल की समांतरता का संकेत: एक रेखा किसी समतल के समानांतर होती है यदि वह इस समतल से संबंधित किसी भी रेखा के समानांतर हो(चित्र 3.12)।

चित्र 3.12 - एक सीधे तल की समांतरता

3.5.2. एक समतल के साथ एक रेखा का प्रतिच्छेदन

एक सामान्य तल के साथ एक सीधी रेखा का प्रतिच्छेदन बिंदु बनाने के लिए (चित्र 3.13), आपको यह करना होगा:

1. सीधे निष्कर्ष निकालें एसहायक विमान β के लिए (विशेष स्थिति के विमानों को सहायक विमान के रूप में चुना जाना चाहिए);
2. दिए गए समतल α के साथ सहायक समतल β की प्रतिच्छेदन रेखा ज्ञात कीजिए;
3. किसी दी गई रेखा का प्रतिच्छेदन बिंदु ज्ञात कीजिए एसमतलों के प्रतिच्छेदन की रेखा के साथ एम.एन..

चित्र 3.13 - एक समतल के साथ एक सीधी रेखा के मिलन बिंदु का निर्माण

व्यायाम

दिया गया: सीधा अबसामान्य स्थिति, समतल σ⊥π 1. (चित्र 3.14)। एक रेखा के प्रतिच्छेदन बिंदु का निर्माण करें अबसमतल σ के साथ.

समाधान :

1. विमान σ क्षैतिज रूप से प्रक्षेपित है, इसलिए, विमान σ का क्षैतिज प्रक्षेपण सीधी रेखा σ 1 (विमान का क्षैतिज निशान) है;
2. डॉट कोलाइन से संबंधित होना चाहिए अब ⇒ को 1 ∈ए 1 में 1 और एक दिया गया समतल σ ⇒ को 1 ∈σ 1 , इसलिए, को 1 प्रक्षेपणों के प्रतिच्छेदन बिंदु पर स्थित है ए 1 में 1 और σ 1 ;
3. बिंदु का ललाट प्रक्षेपण कोहम प्रक्षेपण संचार लाइन के माध्यम से पाते हैं: को 2 ∈ए 2 में 2 .

चित्र 3.14 - एक विशेष तल के साथ एक सामान्य रेखा का प्रतिच्छेदन

व्यायाम

दिया गया: समतल σ = Δ एबीसी- सामान्य स्थिति, सीधी ई.एफ.(चित्र 3.15)।

किसी रेखा के प्रतिच्छेदन बिंदु का निर्माण करना आवश्यक है ई.एफ.समतल σ के साथ.

ए	बी

चित्र 3.15 - एक सीधी रेखा और एक तल का प्रतिच्छेदन

1. आइए एक सीधी रेखा पर निष्कर्ष निकालें ई.एफ.एक सहायक विमान में, जिसके लिए हम क्षैतिज रूप से प्रक्षेपित विमान α का उपयोग करेंगे (चित्र 3.15, ए);
2. यदि α⊥π 1, तो प्रक्षेपण विमान π 1 पर विमान α को एक सीधी रेखा (विमान απ 1 या α 1 का क्षैतिज निशान) में प्रक्षेपित किया जाता है, जो इसके साथ मेल खाता है इ 1 एफ 1 ;
3. आइए समतल σ के साथ प्रक्षेपित समतल α की प्रतिच्छेदन रेखा (1-2) खोजें (एक समान समस्या के समाधान पर विचार किया जाएगा);
4. पंक्ति (1-2) और निर्दिष्ट पंक्ति ई.एफ.एक ही तल α में स्थित हैं और बिंदु पर प्रतिच्छेद करते हैं क.

समस्या को हल करने के लिए एल्गोरिदम (चित्र 3.15, बी):

के माध्यम से ई.एफ.आइए एक सहायक विमान α बनाएं:

3.6. प्रतिस्पर्धी बिंदु पद्धति का उपयोग करके दृश्यता निर्धारण

किसी दी गई रेखा की स्थिति का आकलन करते समय, यह निर्धारित करना आवश्यक है कि प्रक्षेपण विमान π 1 या π 2 को देखते समय, पर्यवेक्षक के रूप में, रेखा का कौन सा बिंदु हमारे करीब (आगे) स्थित है।

वे बिंदु जो विभिन्न वस्तुओं से संबंधित हैं, और प्रक्षेपण विमानों में से एक पर उनके प्रक्षेपण मेल खाते हैं (अर्थात, दो बिंदु एक में प्रक्षेपित होते हैं), इस प्रक्षेपण विमान पर प्रतिस्पर्धा कहलाते हैं.

प्रत्येक प्रक्षेपण तल पर दृश्यता अलग से निर्धारित करना आवश्यक है।

π 2 पर दृश्यता (चित्र 3.15)

आइए हम π 2 - अंक 3 और 4 पर प्रतिस्पर्धा करने वाले बिंदुओं को चुनें। मान लीजिए बिंदु 3∈ है VS∈σ, बिंदु 4∈ ई.एफ..

प्रक्षेपण तल π 2 पर बिंदुओं की दृश्यता निर्धारित करने के लिए, π 2 को देखते समय क्षैतिज प्रक्षेपण तल पर इन बिंदुओं का स्थान निर्धारित करना आवश्यक है।

π 2 की ओर देखने की दिशा तीर द्वारा दर्शाई गई है।

बिंदु 3 और 4 के क्षैतिज प्रक्षेपण से, जब π 2 को देखते हैं, तो यह स्पष्ट होता है कि बिंदु 4 1, 3 1 की तुलना में पर्यवेक्षक के अधिक निकट स्थित है।

4 1 ∈इ 1 एफ 1 ⇒ 4∈ई.एफ.⇒ π 2 पर बिंदु 4 सीधी रेखा पर पड़ा हुआ दिखाई देगा ई.एफ., इसलिए, सीधा ई.एफ.विचाराधीन प्रतिस्पर्धी बिंदुओं के क्षेत्र में σ विमान के सामने स्थित है और बिंदु तक दिखाई देगा क

π 1 पर दृश्यता

दृश्यता निर्धारित करने के लिए, हम उन बिंदुओं का चयन करते हैं जो π 1 - अंक 2 और 5 पर प्रतिस्पर्धा करते हैं।

प्रक्षेपण तल π 1 पर बिंदुओं की दृश्यता निर्धारित करने के लिए, π 1 को देखते समय ललाट प्रक्षेपण तल पर इन बिंदुओं का स्थान निर्धारित करना आवश्यक है।

π 1 की ओर देखने की दिशा तीर द्वारा दर्शाई गई है।

बिंदु 2 और 5 के ललाट प्रक्षेपण से, जब π 1 को देखते हैं, तो यह स्पष्ट होता है कि बिंदु 2 2, 5 2 की तुलना में पर्यवेक्षक के अधिक निकट स्थित है।

2 1 ∈ए 2 में 2 ⇒ 2∈अब⇒ π पर 1 बिंदु 2 सीधी रेखा पर पड़ा हुआ दिखाई देगा अब, इसलिए, सीधा ई.एफ.विचाराधीन प्रतिस्पर्धी बिंदुओं के क्षेत्र में विमान σ के नीचे स्थित है और बिंदु तक अदृश्य रहेगा क– समतल σ के साथ सीधी रेखा के प्रतिच्छेदन बिंदु।

दो प्रतिस्पर्धी बिंदुओं में से दृश्यमान वह होगा जिसका "Z" और/या "Y" निर्देशांक अधिक होगा।

3.7. एक सीधे तल पर लंबवतता

एक सीधे तल की लंबवतता का संकेत: एक रेखा किसी समतल पर लंबवत होती है यदि वह किसी दिए गए समतल में स्थित दो प्रतिच्छेदी रेखाओं पर लंबवत हो।

ए	बी

चित्र 3.16 - समतल पर लंबवत एक सीधी रेखा को परिभाषित करना

प्रमेय. यदि सीधी रेखा समतल के लंबवत है, तो आरेख पर: सीधी रेखा का क्षैतिज प्रक्षेपण समतल के क्षैतिज प्रक्षेपण के लंबवत है, और सीधी रेखा का ललाट प्रक्षेपण समतल के ललाट प्रक्षेपण के लंबवत है ललाट (चित्र 3.16, बी)

प्रमेय को एक विशेष स्थिति में समकोण के प्रक्षेपण पर प्रमेय के माध्यम से सिद्ध किया जाता है।

यदि विमान को निशानों द्वारा परिभाषित किया जाता है, तो विमान के लंबवत सीधी रेखा के प्रक्षेपण विमान के संबंधित निशानों के लंबवत होते हैं (चित्रा 3.16, ए)।

इसे सीधा रहने दो पीसमतल σ=Δ के लंबवत एबीसीऔर बिंदु से होकर गुजरता है क.

1. आइए समतल σ=Δ में क्षैतिज और ललाट रेखाओं का निर्माण करें एबीसी : एक-1∈σ; एक-1//π 1 ; एस 2∈σ; एस 2//π 2 .
2. आइए बिंदु से पुनर्स्थापित करें ककिसी दिए गए विमान के लंबवत: पी 1⊥ज 1और पी2⊥च 2, या पी 1⊥απ 1 और पी2⊥απ 2

3.8. दो तलों की सापेक्ष स्थिति

3.8.1. विमानों की समानता

दो तल समानांतर और प्रतिच्छेदित हो सकते हैं।

दो तलों की समांतरता का संकेत: दो तल परस्पर समानांतर होते हैं यदि एक तल की दो प्रतिच्छेदी रेखाएँ क्रमशः दूसरे तल की दो प्रतिच्छेदी रेखाओं के समानांतर हों।

व्यायाम

सामान्य स्थिति तल α=Δ दिया गया है एबीसीऔर अवधि एफ∉α (चित्र 3.17)।

बिंदु के माध्यम से एफसमतल α के समांतर समतल β खींचिए।

चित्र 3.17 - किसी दिए गए विमान के समानांतर एक विमान का निर्माण

समाधान :

आइए, उदाहरण के लिए, समतल α की प्रतिच्छेदी रेखाओं के रूप में त्रिभुज AB और BC की भुजाओं को लें।

1. बिंदु के माध्यम से एफहम प्रत्यक्ष आचरण करते हैं एम, समानांतर, उदाहरण के लिए, अब.
2. बिंदु के माध्यम से एफ, या किसी भी बिंदु से संबंधित के माध्यम से एम, हम एक सीधी रेखा खींचते हैं एन, समानांतर, उदाहरण के लिए, सूरज, और म∩एन=एफ.
3. β = एम∩एनऔर परिभाषा के अनुसार β//α।

3.8.2. विमानों का प्रतिच्छेदन

दो तलों के प्रतिच्छेदन का परिणाम एक सीधी रेखा है। किसी समतल या अंतरिक्ष में किसी भी सीधी रेखा को दो बिंदुओं द्वारा विशिष्ट रूप से परिभाषित किया जा सकता है। इसलिए, दो तलों के प्रतिच्छेदन की एक रेखा बनाने के लिए, आपको दोनों तलों में दो उभयनिष्ठ बिंदु खोजने चाहिए, और फिर उन्हें जोड़ना चाहिए।

आइए उन्हें परिभाषित करने के विभिन्न तरीकों के साथ दो विमानों के प्रतिच्छेदन के उदाहरणों पर विचार करें: निशानों द्वारा; तीन बिंदु जो एक ही रेखा पर नहीं हैं; समानांतर रेखाएं; प्रतिच्छेदी रेखाएँ, आदि।

व्यायाम

दो तल α और β को निशानों द्वारा परिभाषित किया गया है (चित्र 3.18)। समतलों के प्रतिच्छेदन की एक रेखा का निर्माण करें।

चित्र 3.18 - निशानों द्वारा परिभाषित सामान्य तलों का प्रतिच्छेदन

समतलों के प्रतिच्छेदन की रेखा बनाने की प्रक्रिया:

1. क्षैतिज रेखाओं का प्रतिच्छेदन बिंदु ज्ञात करें - यही बिंदु है एम(उसके अनुमान एम 1 और एम 2, जबकि एम 1 =एम, क्योंकि एम -समतल से संबंधित निजी बिंदु π 1).
2. ललाट पटरियों के प्रतिच्छेदन का बिंदु खोजें - यह बिंदु है एन(उसके अनुमान एन 1 और एन 2, जबकि एन 2 = एन, क्योंकि एन -समतल π 2 से संबंधित निजी बिंदु)।
3. एक ही नाम के परिणामी बिंदुओं के प्रक्षेपणों को जोड़कर विमानों के प्रतिच्छेदन की एक रेखा बनाएं: एम 1 एन 1 और एम 2 एन 2 .

एमएन- समतलों के प्रतिच्छेदन की रेखा।

व्यायाम

दिया गया समतल σ = Δ एबीसी, समतल α - क्षैतिज रूप से प्रक्षेपित (α⊥π 1) ⇒α 1 - समतल का क्षैतिज निशान (चित्र 3.19)।

इन तलों की प्रतिच्छेदन रेखा का निर्माण कीजिए।

समाधान :

चूँकि समतल α भुजाओं को प्रतिच्छेद करता है अबऔर एसीत्रिकोण एबीसी, फिर प्रतिच्छेदन बिंदु कऔर एलसमतल α के साथ ये भुजाएं दोनों दिए गए समतलों के लिए उभयनिष्ठ हैं, जो उन्हें जोड़कर, वांछित प्रतिच्छेदन रेखा खोजने की अनुमति देगा।

बिंदुओं को प्रक्षेपित तल के साथ सीधी रेखाओं के प्रतिच्छेदन बिंदु के रूप में पाया जा सकता है: हम बिंदुओं के क्षैतिज प्रक्षेपण पाते हैं कऔर एल, वह है क 1 और एल 1, पक्षों के क्षैतिज प्रक्षेपण के साथ किसी दिए गए विमान α के क्षैतिज ट्रेस (α 1) के चौराहे पर Δ एबीसी: ए 1 में 1 और ए 1 सी 1 . फिर, प्रक्षेपण संचार लाइनों का उपयोग करके, हम इन बिंदुओं के ललाट प्रक्षेपण पाते हैं K2और एल 2 सीधी रेखाओं के ललाट प्रक्षेपण पर अबऔर एसी. आइए एक ही नाम के प्रक्षेपणों को जोड़ें: क 1 और एल 1 ; K2और एल 2. दिए गए तलों की प्रतिच्छेदन रेखा का निर्माण किया जाता है।

समस्या को हल करने के लिए एल्गोरिदम:

के.एल– प्रतिच्छेदन रेखा Δ एबीसीऔर σ (α∩σ = के.एल).

चित्र 3.19 - सामान्य और विशेष तलों का प्रतिच्छेदन

व्यायाम

दिए गए समतल α = m//n और समतल β = Δ एबीसी(चित्र 3.20)।

दिए गए तलों के प्रतिच्छेदन की एक रेखा बनाएं।

समाधान :

1. दिए गए दोनों तलों में उभयनिष्ठ बिंदुओं को खोजने और तलों α और β की प्रतिच्छेदन रेखा को परिभाषित करने के लिए, विशेष स्थिति के सहायक तलों का उपयोग करना आवश्यक है।
2. ऐसे विमानों के रूप में, हम विशेष स्थिति के दो सहायक विमानों का चयन करेंगे, उदाहरण के लिए: σ // τ; σ⊥π 2 ; τ⊥π 2 .
3. नए पेश किए गए विमान दिए गए प्रत्येक विमान α और β के साथ एक दूसरे के समानांतर सीधी रेखाओं के साथ प्रतिच्छेद करते हैं, क्योंकि σ // τ:

- समतल α, σ और τ के प्रतिच्छेदन का परिणाम सीधी रेखाएं (4-5) और (6-7) हैं;

- समतल β, σ और τ के प्रतिच्छेदन का परिणाम सीधी रेखाएं (3-2) और (1-8) हैं।

1. रेखाएँ (4-5) और (3-2) σ तल में स्थित हैं; उनका प्रतिच्छेदन बिंदु एमएक साथ समतल α और β में स्थित है, अर्थात इन समतलों के प्रतिच्छेदन की सीधी रेखा पर;
2. इसी प्रकार, हम बिंदु पाते हैं एन, α और β तलों के लिए उभयनिष्ठ।
3. बिंदुओं को कनेक्ट करना एमऔर एन, आइए समतल α और β के प्रतिच्छेदन की सीधी रेखा का निर्माण करें।

चित्र 3.20 - सामान्य स्थिति में दो विमानों का प्रतिच्छेदन (सामान्य स्थिति)

समस्या को हल करने के लिए एल्गोरिदम:

व्यायाम

दिए गए समतल α = Δ एबीसीऔर β = ए//बी. दिए गए तलों के प्रतिच्छेदन की एक रेखा बनाएं (चित्र 3.21)।

चित्र 3.21 समतल प्रतिच्छेदन समस्या का समाधान

समाधान :

आइए हम विशेष स्थिति के सहायक छेदक तलों का उपयोग करें। आइए हम उन्हें इस तरह से पेश करें जिससे निर्माणों की संख्या कम हो सके। उदाहरण के लिए, आइए सीधी रेखा को घेरते हुए समतल σ⊥π 2 का परिचय दें एसहायक विमान में σ (σ∈ ए). समतल σ, समतल α को एक सीधी रेखा (1-2) के अनुदिश काटता है, और σ∩β= ए. इसलिए (1-2)∩ ए=क.

डॉट कोदोनों तलों α और β से संबंधित है।

इसलिए, बात क, आवश्यक बिंदुओं में से एक है जिसके माध्यम से दिए गए विमानों α और β की प्रतिच्छेदन रेखा गुजरती है।

α और β की प्रतिच्छेदन रेखा से संबंधित दूसरा बिंदु खोजने के लिए, हम रेखा को समाप्त करते हैं बीसहायक तल में τ⊥π 2 (τ∈ बी).

बिंदुओं को कनेक्ट करना कऔर एल, हम समतल α और β के प्रतिच्छेदन की सीधी रेखा प्राप्त करते हैं।

3.8.3. परस्पर लंबवत विमान

यदि उनमें से एक दूसरे के लंबवत से होकर गुजरता है तो विमान परस्पर लंबवत होते हैं।

व्यायाम

सामान्य स्थिति में एक समतल σ⊥π 2 और एक रेखा दी गई है - डे(चित्र 3.22)

के माध्यम से निर्माण करना आवश्यक है डेविमान τ⊥σ.

समाधान ।

आइए एक लंब बनाएं सीडीविमान के लिए σ – सी 2 डी 2 ⊥σ 2 (पर आधारित)।

चित्र 3.22 - किसी दिए गए समतल के लंबवत समतल का निर्माण

समकोण प्रक्षेपण प्रमेय द्वारा सी 1 डी 1 प्रक्षेपण अक्ष के समानांतर होना चाहिए। प्रतिच्छेदी रेखाएँ सीडी∩डेसमतल को परिभाषित करें τ. तो, τ⊥σ।

सामान्य तल के मामले में भी ऐसा ही तर्क।

व्यायाम

दिया गया समतल α = Δ एबीसीऔर अवधि कα तल के बाहर.

बिंदु से गुजरने वाले एक समतल β⊥α का निर्माण करना आवश्यक है क.

समाधान एल्गोरिथ्म(चित्र 3.23):

1. आइए एक क्षैतिज रेखा बनाएं एचऔर सामने एफकिसी दिए गए विमान में α = Δ एबीसी;
2. बिंदु के माध्यम से कआइए एक लंब बनाएं बीसमतल α तक (साथ में समतल प्रमेय के लंबवत: यदि एक सीधी रेखा किसी समतल पर लंबवत है, तो उसके प्रक्षेपण समतल में पड़ी क्षैतिज और ललाट रेखाओं के झुके हुए प्रक्षेपणों के लंबवत होते हैं:बी 2⊥च 2; बी 1⊥ज 1;
3. हम समतल β को किसी भी तरह से परिभाषित करते हैं, उदाहरण के लिए, β = ए∩बी, इस प्रकार, दिए गए विमान के लंबवत एक विमान का निर्माण किया जाता है: α⊥β।

चित्र 3.23 - किसी दिए गए Δ के लंबवत समतल का निर्माण एबीसी

3.9. स्वतंत्र रूप से हल करने योग्य समस्याएं

1. दिया गया समतल α = एम//एन(चित्र 3.24)। ह ज्ञात है कि क∈α.

एक बिंदु के ललाट प्रक्षेपण का निर्माण करें को.

चित्र 3.24

2. एक खंड द्वारा दी गई सीधी रेखा के निशान बनाएं सी.बी., और उन चतुर्थांशों की पहचान करें जिनसे यह गुजरता है (चित्र 3.25)।

चित्र 3.25

3. समतल α⊥π 2 से संबंधित एक वर्ग के प्रक्षेपण का निर्माण करें यदि इसका विकर्ण एम.एन.//π 2 (चित्र 3.26)।

चित्र 3.26

4. एक आयत की रचना कीजिए ए बी सी डीबड़े पक्ष के साथ सूरजएक सीधी रेखा पर एम, इस शर्त के आधार पर कि इसकी भुजाओं का अनुपात 2 है (चित्र 3.27)।

चित्र 3.27

5. दिया गया समतल α= ए//बी(चित्र 3.28)। समतल α के समांतर और उससे 20 मिमी की दूरी पर एक समतल β की रचना कीजिए।

चित्र 3.28

6. दिया गया समतल α=∆ एबीसीऔर अवधि डी डीसमतल β⊥α तथा β⊥π 1।

7. दिया गया समतल α=∆ एबीसीऔर अवधि डीहवाई जहाज से बाहर। बिंदु के माध्यम से निर्माण करें डीप्रत्यक्ष डे//α और डे//π 1 .

अंतरिक्ष में विमान की स्थिति ज्यामिति में प्रसिद्ध तत्वों में से एक द्वारा विशिष्ट रूप से निर्धारित की जा सकती है। इसके अनुसार, विमान को छह तरीकों में से एक में निर्दिष्ट किया जा सकता है:

क) तीन बिंदु जो एक ही रेखा पर नहीं हैं;

बी) एक रेखा और एक बिंदु जो इस रेखा पर नहीं है;

ग) दो समानांतर रेखाएँ;

घ) दो प्रतिच्छेदी रेखाएँ;

ई) सपाट आकृति;

ई) निशान।

फिर चित्र (चित्र 3.1) में संबंधित ज्यामितीय वस्तुएँ (बिंदु, रेखाएँ) प्रक्षेपण की तरह दिखती हैं।

चावल। 3.1. एक तल को परिभाषित करने वाली ज्यामितीय वस्तुओं का धुरा-मुक्त दो-चित्र जटिल चित्रण।

3.2. विशेष और सामान्य विमान

3.2.1. समतल विमान

एक समतल विमान प्रक्षेपण विमानों में से एक के समानांतर एक विमान है, और इसलिए अन्य दो के लंबवत है। फिर समतल समतल के प्रक्षेपण संगत अक्षों के समानांतर सीधी रेखाएं होंगी (चित्र 3.2), चाहे समतल को कैसे भी परिभाषित किया गया हो। केवल उस प्रक्षेपण तल पर इसका प्रक्षेपण जिसके समानांतर दिया गया तल है, तल को निर्दिष्ट करने की विधि पर निर्भर करता है।

विमान समानांतर पी 1, को क्षैतिज स्तर का तल कहा जाता है ( जी). चित्र में. 3.2a इसे तीन बिंदुओं द्वारा परिभाषित किया गया है।

विमान समानांतर पी 2, को ललाट स्तर का तल कहा जाता है ( एफ). आइए इसे समानांतर रेखाओं द्वारा परिभाषित करें (चित्र 3.2बी)।

विमान समानांतर पी 3, को लेवल प्रोफाइल प्लेन कहा जाता है ( आर). हम इसे सीधी रेखाओं को प्रतिच्छेद करके दिए गए मान पर विचार करते हैं (चित्र 3.2c)।

चावल। 3.2. एक जटिल ड्राइंग में समतल समतल।

3.2.2. प्रक्षेपण विमान

एक प्रक्षेपित विमान प्रक्षेपण विमानों में से एक के लंबवत एक विमान है। परिभाषा के आधार पर, ऐसा विमान एक सीधी रेखा में परिवर्तित हो जाता है जब इसे उस प्रक्षेपण विमान पर प्रक्षेपित किया जाता है जिस पर यह लंबवत होता है।

चावल। 3.3. एक जटिल रेखाचित्र में विमानों को प्रक्षेपित करना।

क्षैतिज रूप से प्रक्षेपित एक समतल एक लंबवत समतल होता है पी 1, अग्र-प्रक्षेपण - लंबवत पी 2, और प्रोफाइल-प्रोजेक्टिंग - एक समतल लंबवत पी 3. चित्र में, उनमें से पहले को एक सपाट आकृति (चित्र 3.3a) द्वारा परिभाषित किया गया है, दूसरे को एक बिंदु और एक सीधी रेखा (चित्र 3.3b) द्वारा, और तीसरे को दो समानांतर सीधी रेखाओं (चित्र 3.3c) द्वारा परिभाषित किया गया है। ).

3.2.3. सामान्य विमान

एक सामान्य विमान एक ऐसा विमान है जो किसी भी प्रक्षेपण विमान के लिए न तो लंबवत है और न ही समानांतर है, और इसलिए उनमें से प्रत्येक के लिए एक मनमाना कोण पर स्थित है।

ऐसे समतल में सभी प्रक्षेपण समतल आकृतियों के रूप में होंगे (चित्र 3.4)।

चावल। 3.4. सामान्य तल को एक त्रिभुज द्वारा परिभाषित किया गया है

3.3. एक बिंदु और एक सीधे तल का संबंध

एक बिंदु एक समतल का होता है यदि वह इस तल में पड़ी किसी रेखा से संबंधित हो। एक सीधे विमान से संबंधित होना दो मानदंडों में से एक द्वारा निर्धारित किया जाता है:

क) एक सीधी रेखा इस तल में स्थित दो बिंदुओं से होकर गुजरती है;

बी) एक रेखा एक बिंदु से होकर गुजरती है और इस तल में पड़ी रेखाओं के समानांतर होती है।

3.4. मुख्य समतल रेखाएँ

किसी समतल की मुख्य रेखाएँ किसी दिए गए समतल में स्थित समतल रेखाएँ होती हैं। आइए त्रिभुज द्वारा परिभाषित समतल की मुख्य रेखाओं के निर्माण पर विचार करें (चित्र 3.5)।

क्षैतिज समक्षेत्र डीएबीसीहम इसके ललाट प्रक्षेपण को चित्रित करके प्रारंभ करते हैं एच 2, जिसे अक्ष के समानांतर माना जाता है ओह. चूँकि यह क्षैतिज रेखा इसी समतल की है, यह समतल के दो बिंदुओं से होकर गुजरती है डीएबीसी, अर्थात्, अंक एऔर 1. उनके ललाट प्रक्षेपण होना ए 2 और 1 2, संचार लाइन के साथ हम क्षैतिज प्रक्षेपण 1 1 प्राप्त करते हैं। बिंदुओं को कनेक्ट करना ए 1 और 1 1, हमारे पास एक क्षैतिज प्रक्षेपण है एच 1 क्षैतिज तल डीएबीसी. प्रोफ़ाइल प्रक्षेपण एच 3 क्षैतिज तल डीएबीसीअक्ष के समानांतर होगा ओहएक-प्राथमिकता.

सामने का विमान डीएबीसीइसका निर्माण एक समान तरीके से किया गया है (चित्र 3.5) केवल अंतर के साथ कि इसका चित्रण क्षैतिज प्रक्षेपण से शुरू होता है एफ 1, चूँकि यह ज्ञात है कि यह OX अक्ष के समानांतर है। प्रोफ़ाइल प्रक्षेपण एफफ्रंट 3 OZ अक्ष के समानांतर होना चाहिए।

विमान की प्रोफाइल लाइन डीएबीसीएक क्षैतिज है आर 1 और सामने आरअक्षों के समानांतर 2 प्रक्षेपण ओएऔर आउंस, और प्रोफ़ाइल प्रक्षेपण आर 3 को प्रतिच्छेदन बिंदुओं का उपयोग करके सामने से प्राप्त किया जा सकता है मेंऔर 3 एस डी एबीसी.

किसी समतल की मुख्य रेखाओं का निर्माण करते समय, आपको केवल एक नियम याद रखना होगा: समस्या को हल करने के लिए आपको हमेशा किसी दिए गए समतल के साथ प्रतिच्छेदन के दो बिंदु प्राप्त करने होंगे।

चावल। 3.5. एक त्रिभुज द्वारा परिभाषित समतल की मुख्य रेखाओं का निर्माण

3.5. सीधी रेखाओं और तलों की पारस्परिक स्थिति

3.5.1. रेखाओं और तलों की समानता

ए)। यदि रेखाएँ एक दूसरे के समानांतर हैं, तो एक ही नाम के उनके प्रक्षेपण समानांतर होते हैं। बी)। एक रेखा किसी समतल के समानांतर होती है यदि वह इस तल में पड़ी किसी रेखा के समानांतर हो

चावल। 3.6. समानांतर ज्यामितीय वस्तुओं का निर्माण.

फिर एक समानांतर रेखा बनाएं ए(चित्र 3.6ए) यह आवश्यक है कि इसके दोनों प्रक्षेपण सीधी रेखा के समान प्रक्षेपणों के समानांतर हों (उदाहरण के लिए, अब) इस विमान में लेटा हुआ। ग) विमान एक दूसरे के समानांतर होते हैं यदि एक विमान की दो प्रतिच्छेदी रेखाएं दूसरे विमान की दो प्रतिच्छेदी रेखाओं के जोड़ीवार समानांतर होती हैं। इस संपत्ति की व्याख्या करने के लिए, चित्र में निर्माणों को पूरक करना पर्याप्त है। 3.6a एक और सीधी रेखा वी,क्रॉसिंग एऔर समानांतर सूरज(चित्र 3.6बी)।

3.5.2. रेखाओं और तलों की लंबवतता

ए)। एक रेखा किसी तल पर लंबवत होती है यदि वह इस तल में पड़ी दो प्रतिच्छेदी रेखाओं पर लंबवत होती है, जिनमें से एक ललाट और दूसरी क्षैतिज होती है।

यद्यपि लंबवतता के लिए यह काफी है कि संकेतित प्रतिच्छेदी रेखाएं किसी दिए गए विमान में कोई भी सीधी रेखाएं हों, तथापि, केवल क्षैतिज और ललाट ही विमान और ललाट के लंबवत द्वारा बनाए गए समकोण के विरूपण के बिना प्रक्षेपण प्राप्त करने की अनुमति देते हैं। (पर पी 2) और समतल के लंबवत और क्षैतिज (पर पी 1). तब यह स्पष्ट है कि इस लम्ब का क्षैतिज प्रक्षेपण क्षैतिज के क्षैतिज प्रक्षेपण के समकोण पर स्थित है, और ललाट का प्रक्षेपण ललाट के ललाट प्रक्षेपण के समकोण पर है।

चावल। 3.7. लंबवत स्थित ज्यामितीय वस्तुओं का निर्माण।

बी)। विमान एक-दूसरे के लंबवत होते हैं यदि उनमें से एक में दूसरे पर लंबवत होता है।

आइए चित्र देखें। 3.7ए, जहां लंबवत है जीविमान का निर्माण पहले ही हो चुका है, यह एक बिंदु के माध्यम से आवश्यक है डीएक मनमाना सीधी रेखा खींचें क्यू(चित्र 3.7बी)।

3.6. एक विमान पर स्थितीय समस्याएं

स्थिति संबंधी कार्यों को ज्यामितीय वस्तुओं के किसी भी सामान्य तत्व को निर्धारित करने के कार्य कहा जाता है, उदाहरण के लिए, एक सीधी रेखा और एक विमान का प्रतिच्छेदन बिंदु, दो विमानों के प्रतिच्छेदन की रेखा।

3.6.1. एक रेखा और एक समतल का प्रतिच्छेदन

एक रेखा और एक विमान के प्रतिच्छेदन की समस्या को एक सहायक कटिंग विमान का उपयोग करके हल किया जा सकता है, जिसे निम्नलिखित शर्तों को पूरा करना होगा:

क) विशेष स्थिति का एक विमान हो, क्योंकि यह विशेष स्थिति का विमान है जो एक सीधी रेखा के रूप में प्रक्षेपण के संबंधित विमान पर प्रक्षेपित होता है;

बी) एक सीधी रेखा से गुजरें, जिस विमान की हम तलाश कर रहे हैं उसके साथ उसका प्रतिच्छेदन बिंदु।

आइए पहले एक विशेष मामले पर विचार करें। उदाहरण के लिए, विमान को अंतरिक्ष में एक विशेष स्थिति पर कब्जा करने दें, क्षैतिज रूप से प्रक्षेपित किया जाए और एक त्रिकोण द्वारा परिभाषित किया जाए एबीसी(चित्र 3.8 ए)। रेखा के साथ इसका प्रतिच्छेदन बिंदु ज्ञात करना आवश्यक है ए, मनमाने ढंग से दिया गया। तब से पी 1 क्षैतिज रूप से प्रक्षेपित तल एक सीधी रेखा S 1 में परिवर्तित हो जाता है, तो प्रतिच्छेदन बिंदु का क्षैतिज प्रक्षेपण होगा को 1 . आगे संचार लाइन के साथ सीधी लाइन पर ए 2 (स्पष्ट रूप से प्रतिच्छेदन बिंदु कोरेखा से संबंधित है ए) ललाट प्रक्षेपण खोजें को 2 प्रतिच्छेदन बिंदु.

यह सीधी रेखा के दृश्यमान वर्गों को निर्धारित करने के लिए बना हुआ है ए, क्योंकि पर पीसंकेतित रेखा का भाग 2 विमान द्वारा पर्यवेक्षक से छिपाया जाएगा डीएबीसी. ऐसा करने के लिए, उस बिंदु पर विचार करना आवश्यक है जहां ललाट प्रक्षेपण प्रतिच्छेद करते हैं एऔर कोई प्रत्यक्ष (उदाहरण के लिए, एसी), विमान में लेटा हुआ डीएबीसी. आइए इस बिंदु को 1 2 से निरूपित करें। लेकिन सीधी रेखा a और प्रतिच्छेद करती है डीएबीसीकेवल एक ही बिंदु पर हो सकता है जो हमने पाया ( को 2). अन्य सभी बिंदु वे बिंदु होंगे जहां वे प्रतिच्छेद करते हैं। इसलिए, सीधे एऔर एसीअंतरिक्ष में प्रतिच्छेद करें. इसका मतलब यह है कि वे सभी बिंदु जहां उनके प्रक्षेपण प्रतिच्छेद करते हैं, प्रतिस्पर्धात्मक होंगे, अर्थात् 1 2 =2 2। तब से पी 1 हमारे पास संचार लाइन 1 1 ओ के माध्यम से है ए 1 साथ 1 और 2 1 ओ ए 1 . दृश्यमान बिंदु 2 है, जो रेखा से संबंधित है ए. यह चौराहा बिंदु तक बना रहता है को 2. फिर, स्वाभाविक रूप से, सीधा खंड एविमान छोड़ने तक अदृश्य रहेगा (एक बिंदीदार रेखा द्वारा दर्शाया गया)। डीएबीसी. अब समस्या पूरी तरह सुलझी हुई मानी जा सकती है.

आइए एक रेखा और एक तल के प्रतिच्छेदन के सामान्य मामले पर विचार करें, जब वे दोनों अंतरिक्ष में एक सामान्य स्थिति पर कब्जा कर लेते हैं। मान लीजिए कि समतल को एक त्रिभुज द्वारा परिभाषित किया गया है डीएबीसी. यहां और आगे हम मुख्य रूप से एक त्रिभुज द्वारा समतल की परिभाषा का उपयोग करेंगे, क्योंकि इस मामले में समस्या का समाधान सबसे स्पष्ट है। किसी मनमाने ढंग से दी गई रेखा का प्रतिच्छेदन बिंदु ज्ञात करना आवश्यक है वीसाथ डीएबीसी(चित्र 3.8, बी)।

जैसा ऊपर बताया गया है, आपको सीधे इसकी आवश्यकता है वीविशेष स्थिति का एक विमान बनाएं (उदाहरण के लिए, सामने से प्रक्षेपित करना)। इस तल की प्रतिच्छेदन रेखा सीधी रेखा से मेल खाती है वीपर पी 2, यानी एस 2 = वी 2. फिर, प्रतिच्छेदन बिंदु 3 2 और 4 2 का उपयोग करके, हम बिंदु 3 1 और 4 1 का निर्माण करते हैं, और इसलिए सीधी रेखा 3 1 4 1, जो कि समतल S और के प्रतिच्छेदन रेखा का क्षैतिज प्रक्षेपण है। डीएबीसी. लेकिन चूँकि सीधी रेखा 34Ì है डीएबीसी,तब बिंदु K 1 रेखा के प्रतिच्छेदन बिंदु का क्षैतिज प्रक्षेपण होगा वीऔर डीएबीसी।इसका उपयोग करके हम ललाट प्रक्षेपण पाएंगे को 2, जो स्पष्टतः पर स्थित होना चाहिए वी 2 (आखिरकार, प्रतिच्छेदन बिंदु भी रेखा से संबंधित है वीऔर डी एबीसी)।

चावल। 3.8. एक रेखा और एक समतल का प्रतिच्छेदन

आइए सीधी रेखा के दृश्यमान खंडों को निर्धारित करें वीप्रतिस्पर्धी बिंदुओं पर दोनों अनुमानों पर। दृश्यता निर्धारित करने के लिए पी 2 हम सामने से प्रतिस्पर्धी बिंदुओं का उपयोग करते हैं (उदाहरण के लिए, बिंदु 3 2 =5 2, जहां वे पार करते हैं वी 2 और ए 2 में 2). जाहिर है, बिंदु 31, बिंदु 51 की तुलना में हमारे अधिक निकट है। इसलिए, पर पी 2 ऊपर 3 2 फिर इस बिंदु पर ए 2 में 2 ऊपर और वी 2 इसके नीचे स्थित है। यह केवल प्रतिच्छेदन बिंदु तक ही सत्य है को 2. आगे, स्वाभाविक रूप से, यह अधिक होगा वी 2. इसी प्रकार, क्षैतिज रूप से प्रतिस्पर्धी बिंदुओं (उदाहरण के लिए, 6 1 =7 1) का उपयोग करके, हम यह निर्धारित करते हैं कि बिंदु 6 1 =7 1 पर एक सीधी रेखा है में 1 साथ 1 से ऊँचा है वी 1, चूँकि बिंदु 7 2, बिंदु 6 2 से ऊँचा स्थित है। अदृश्य सीधा खंड वीएक बिंदीदार रेखा द्वारा निरूपित।

3.6.2. विमानों का प्रतिच्छेदन। सहायक काटने वाले विमानों की विधि

चूँकि दो तलों की प्रतिच्छेदन रेखा एक सीधी रेखा है, इसलिए इसे बनाने के लिए तलों के प्रतिच्छेदन के केवल दो बिंदु निर्धारित करना आवश्यक है।

इस समस्या को हल करने के लिए सहायक कटिंग विमानों की विधि का उपयोग किया जाता है, जो इस प्रकार है।

दो अतिरिक्त तल लाए गए हैं जो दिए गए तलों को काटते हैं। प्रत्येक अतिरिक्त (सहायक) तल के लिए, हम दिए गए तलों के साथ उसके प्रतिच्छेदन की एक रेखा बनाते हैं। दो परिणामी रेखाओं का प्रतिच्छेदन बिंदु दिए गए तलों का प्रतिच्छेदन बिंदु होगा। चूँकि दो अतिरिक्त तल हैं, इसलिए दिए गए तलों के प्रतिच्छेदन बिंदु भी दो हैं। इन्हें जोड़ने पर हमें समतलों की प्रतिच्छेदन रेखा प्राप्त होती है। बेशक, प्रत्येक अतिरिक्त विमान को अंतरिक्ष में एक विशेष स्थिति पर कब्जा करना चाहिए, फिर प्रक्षेपण विमान पर जिस पर सहायक विमान लंबवत है, इसे एक सीधी रेखा में प्रक्षेपित किया जाता है। अन्यथा, यदि सहायक विमान एक सामान्य स्थिति रखता है, तो एक अतिरिक्त विमान पेश करने से समस्या का समाधान सरल नहीं होता है।

आइए दो उदाहरणों से स्पष्ट करें।

दो त्रिभुजों की प्रतिच्छेदन रेखा ज्ञात कीजिए एबीसीऔर डीईएफ़और पक्षों की दृश्यता निर्धारित करें (चित्र 3.9)। आइए अतिरिक्त कटिंग विमानों की विधि का उपयोग करके त्रिभुजों के प्रतिच्छेदन की एक रेखा बनाएं। समस्या के समाधान को सरल बनाने के लिए, हम त्रिभुजों की भुजाओं से होकर काटने वाले तल खींचेंगे।

चावल। 3.9. दो त्रिभुजों का प्रतिच्छेदन

एक अतिरिक्त क्षैतिज रूप से प्रक्षेपित विमान S को किनारे से गुजरने दें डे. तब एस 1 = डी 1 इ 1 . यह S के प्रतिच्छेदन रेखा का क्षैतिज प्रक्षेपण है डीएबीसीऔर डीडीईएफ. आइए एक ललाट प्रक्षेपण बनाएं। के लिए डीडीईएफयह स्पष्ट है डी 2 इ 2. के लिए डीएबीसीप्रतिच्छेदन बिंदुओं के क्षैतिज प्रक्षेपण 1 1 और 2 1 का उपयोग करते हुए, हम उनके ललाट प्रक्षेपण 1 2 और 2 2 पाते हैं, जिन्हें जोड़ने पर हम विमान एस के प्रतिच्छेदन की रेखा का ललाट प्रक्षेपण प्राप्त करते हैं और डीएबीसी. पंक्तियों का विस्तार डी 2 इ 2 और 1 2 2 2, उनका प्रतिच्छेदन बिंदु ज्ञात कीजिए एन 2*, जो त्रिभुजों द्वारा परिभाषित तलों का प्रतिच्छेदन बिंदु है। यह ध्यान दिया जाना चाहिए कि बिंदु एन 2 * त्रिभुजों से संबंधित नहीं है, और इसलिए यह त्रिभुजों का नहीं, बल्कि उन तलों का प्रतिच्छेदन बिंदु है जिनमें त्रिभुज स्थित हैं।

इसी तरह, किनारे से गुजरते हुए एक अतिरिक्त क्षैतिज रूप से प्रक्षेपित विमान S* का परिचय दिया जा रहा है सूरजत्रिकोण एबीसी, आइए एक बिंदु खोजें एमदिए गए त्रिभुजों के 2 प्रतिच्छेदन।

बिंदुओं को कनेक्ट करना एन 2* और एम 2, त्रिभुजों के तलों की प्रतिच्छेदन रेखा का ललाट प्रक्षेपण ज्ञात कीजिए एबीसीऔर डीईएफ.एक क्षेत्र का चयन कर लिया है एन 2 एम 2, दोनों त्रिभुजों के तल में स्थित होने पर, हमें त्रिभुजों की प्रतिच्छेदन रेखा का एक ललाट प्रक्षेपण प्राप्त होता है एबीसीऔर डीईएफ.धाराओं से एन 2 एम 2, हम क्षैतिज प्रक्षेपण को भी परिभाषित करते हैं एन 1 एमदिए गए त्रिभुजों के प्रतिच्छेदन की 1 रेखाएँ। यह ध्यान दिया जाना चाहिए कि हमने अतिरिक्त विमानों को पूरी तरह से मनमाने ढंग से चुना। भुजाओं की दृश्यता, और उनके साथ त्रिभुजों के अलग-अलग हिस्सों की दृश्यता, प्रतिस्पर्धी बिंदुओं का उपयोग करके निर्धारित की जाती है। ऐसे दो बिंदु पहले से मौजूद हैं (2 1 =3 1)। ललाट प्रक्षेपणों की जांच से, यह स्पष्ट है कि 2 1 अदृश्य है। इसका मतलब यह है कि इस बिंदु पर सीधी रेखा है डी 1 इ 1 ऊपर में 1 साथ 1, और इसलिए, यह त्रिभुज के तल के बाद से, पूरी लंबाई के साथ अधिक है डीए 1 में 1 साथ 1 कहीं भी प्रतिच्छेद नहीं करता. फिर दूसरी तरफ एन 1 एम 1 त्रिभुज तल डी 1 इ 1 एफ 1 कम होगा. इसी प्रकार, हम प्रतिच्छेदी रेखाओं पर सह-घटित बिंदु 5 और 6 पर विचार करते हुए, ललाट प्रक्षेपण पर दृश्यता निर्धारित करते हैं डेऔर अब(चित्र 3.9)। दृश्यता निर्धारित करने में कठिनाइयों के मामले में, आप दिए गए त्रिभुजों की प्रतिच्छेदी भुजाओं के कई युग्मों का उपयोग कर सकते हैं।

अंतरिक्ष में विमान की स्थिति को निम्नलिखित में से किसी एक तरीके से चित्र में निर्धारित किया जा सकता है:

1. तीन बिंदु जो एक ही रेखा पर नहीं हैं ( चावल। 35).

2. एक रेखा और एक बिंदु जो इस रेखा पर नहीं है ( चावल। 36).

3. दो प्रतिच्छेदी रेखाएँ ( चावल। 37).

4. दो समानांतर रेखाएँ (चित्र। 38 ).

5. सपाट आकृति ( चावल। 39).

6. निशान ( चावल। 40, 41).

7. समतल पैरामीटर.

विमान के निशान

विमान का पीछा कर रहे हैंप्रक्षेपण तल के साथ समतल की प्रतिच्छेदन रेखा कहलाती है . एक विमान के निशान को विमान के समान अक्षर द्वारा दर्शाया जाता है, जिसमें प्रक्षेपण विमान के नाम के अनुरूप एक सबस्क्रिप्ट होता है जिसके साथ यह प्रतिच्छेद करता है। यदि विमान (आइए इसे कॉल करें पी ) किसी भी प्रक्षेपण तल के समानांतर नहीं है, तो यह सभी तीन प्रक्षेपण तलों को काटता है और इसलिए, इसमें तीन निशान होते हैं - क्षैतिज पी एच , ललाट पी वी और प्रोफ़ाइल पी डब्ल्यू (चावल। 40, 41). किसी भी सीधी रेखा की तरह, किसी समतल के किसी भी निशान में तीन प्रक्षेपण होते हैं, लेकिन, आरेख को पढ़ने में आसान बनाने के लिए, निशान के केवल उस प्रक्षेपण को नामित करने की प्रथा है जो प्रक्षेपण के अक्ष के साथ मेल नहीं खाता है। किसी भी सीधी रेखा की तरह, किसी भी विमान के निशान की स्थिति उसके दो बिंदुओं की स्थिति से निर्धारित होती है। किसी समतल के निशानों के लिए, ऐसे बिंदुओं को बिंदु कहा जा सकता है लुप्त बिंदु, अर्थात्, वे बिंदु जिन पर तल निर्देशांक अक्षों को प्रतिच्छेद करता है - पी एक्स ,पाय ,पी ज़ेड . निर्देशांक के संख्यात्मक मान एक्स , य , और जेड निशानों के लुप्त बिंदु कहलाते हैं समतल पैरामीटर.

प्लैनिमेट्री में विमान मुख्य आकृतियों में से एक है, इसलिए इसकी स्पष्ट समझ होना बहुत जरूरी है। यह आलेख इस विषय को कवर करने के लिए बनाया गया था. सबसे पहले, एक विमान की अवधारणा, उसका ग्राफिकल प्रतिनिधित्व दिया गया है और विमानों के पदनाम दिखाए गए हैं। इसके बाद, विमान को एक बिंदु, एक सीधी रेखा या किसी अन्य विमान के साथ माना जाता है, और अंतरिक्ष में सापेक्ष स्थिति से विकल्प उत्पन्न होते हैं। लेख के दूसरे और तीसरे और चौथे पैराग्राफ में, दो विमानों, एक सीधी रेखा और एक विमान, साथ ही बिंदुओं और विमानों की सापेक्ष स्थिति के सभी विकल्पों का विश्लेषण किया गया है, मूल सिद्धांतों और ग्राफिक चित्रण दिए गए हैं। निष्कर्ष में, अंतरिक्ष में एक विमान को परिभाषित करने की मुख्य विधियाँ दी गई हैं।

पेज नेविगेशन.

समतल - बुनियादी अवधारणाएँ, प्रतीक और छवियाँ।

त्रि-आयामी अंतरिक्ष में सबसे सरल और सबसे बुनियादी ज्यामितीय आकृतियाँ एक बिंदु, एक सीधी रेखा और एक तल हैं। हमें पहले से ही समतल पर एक बिंदु और एक रेखा का अंदाज़ा है। यदि हम एक समतल रखें जिस पर त्रि-आयामी अंतरिक्ष में बिंदुओं और रेखाओं को दर्शाया गया है, तो हमें अंतरिक्ष में बिंदु और रेखाएँ मिलती हैं। अंतरिक्ष में एक विमान का विचार हमें, उदाहरण के लिए, एक मेज या दीवार की सतह प्राप्त करने की अनुमति देता है। हालाँकि, एक मेज या दीवार के आयाम सीमित होते हैं, और तल अपनी सीमाओं से परे अनंत तक फैला होता है।

अंतरिक्ष में बिंदुओं और रेखाओं को उसी तरह नामित किया जाता है जैसे एक विमान पर - क्रमशः बड़े और छोटे लैटिन अक्षरों में। उदाहरण के लिए, बिंदु A और Q, रेखाएँ a और d। यदि एक रेखा पर दो बिंदु दिए गए हैं, तो रेखा को इन बिंदुओं के अनुरूप दो अक्षरों से दर्शाया जा सकता है। उदाहरण के लिए, सीधी रेखा AB या BA बिंदु A और B से होकर गुजरती है। विमानों को आमतौर पर छोटे ग्रीक अक्षरों से दर्शाया जाता है, उदाहरण के लिए, विमान, या।

समस्याओं को हल करते समय, विमानों को चित्र में चित्रित करना आवश्यक हो जाता है। एक समतल को आमतौर पर एक समांतर चतुर्भुज या एक मनमाना सरल बंद क्षेत्र के रूप में दर्शाया जाता है।

एक तल को आमतौर पर बिंदुओं, सीधी रेखाओं या अन्य तलों के साथ माना जाता है, और उनकी सापेक्ष स्थिति के लिए विभिन्न विकल्प सामने आते हैं। आइए उनके विवरण पर आगे बढ़ें।

समतल और बिंदु की सापेक्ष स्थिति.

आइए स्वयंसिद्ध से शुरू करें: प्रत्येक तल में बिंदु होते हैं। इससे विमान और बिंदु की सापेक्ष स्थिति के लिए पहला विकल्प आता है - बिंदु विमान से संबंधित हो सकता है। दूसरे शब्दों में, एक विमान एक बिंदु से गुजर सकता है। यह इंगित करने के लिए कि एक बिंदु एक समतल से संबंधित है, प्रतीक "" का उपयोग किया जाता है। उदाहरण के लिए, यदि विमान बिंदु A से होकर गुजरता है, तो आप संक्षेप में लिख सकते हैं।

यह समझा जाना चाहिए कि अंतरिक्ष में किसी दिए गए तल पर अनंत रूप से कई बिंदु हैं।

निम्नलिखित स्वयंसिद्ध दर्शाता है कि एक विशिष्ट विमान को परिभाषित करने के लिए अंतरिक्ष में कितने बिंदुओं को चिह्नित किया जाना चाहिए: तीन बिंदुओं के माध्यम से जो एक ही रेखा पर नहीं हैं, एक विमान गुजरता है, और केवल एक। यदि किसी समतल में स्थित तीन बिंदु ज्ञात हों, तो समतल को इन बिंदुओं के संगत तीन अक्षरों से दर्शाया जा सकता है। उदाहरण के लिए, यदि कोई विमान बिंदु A, B और C से होकर गुजरता है, तो इसे ABC नामित किया जा सकता है।

आइए हम एक और स्वयंसिद्ध सूत्र तैयार करें, जो विमान और बिंदु की सापेक्ष स्थिति का दूसरा संस्करण देता है: कम से कम चार बिंदु हैं जो एक ही विमान में नहीं हैं। तो, अंतरिक्ष में एक बिंदु विमान से संबंधित नहीं हो सकता है। दरअसल, पिछले सिद्धांत के आधार पर, एक विमान अंतरिक्ष में तीन बिंदुओं से होकर गुजरता है, और चौथा बिंदु इस विमान पर स्थित हो भी सकता है और नहीं भी। संक्षेप में लिखते समय, प्रतीक "" का उपयोग करें, जो "संबंधित नहीं है" वाक्यांश के बराबर है।

उदाहरण के लिए, यदि बिंदु A समतल में नहीं है, तो संक्षिप्त नोटेशन का उपयोग करें।

अंतरिक्ष में सीधी रेखा और समतल.

सबसे पहले, एक सीधी रेखा एक समतल में स्थित हो सकती है। इस स्थिति में, इस रेखा के कम से कम दो बिंदु समतल में स्थित होते हैं। यह स्वयंसिद्ध सूत्र द्वारा स्थापित किया गया है: यदि एक रेखा के दो बिंदु एक तल में स्थित हैं, तो इस रेखा के सभी बिंदु एक तल में स्थित हैं। किसी दिए गए तल से किसी निश्चित रेखा के संबंध को संक्षेप में रिकॉर्ड करने के लिए, प्रतीक "" का उपयोग करें। उदाहरण के लिए, संकेतन का अर्थ है कि सीधी रेखा a समतल में स्थित है।

दूसरे, एक सीधी रेखा किसी समतल को काट सकती है। इस मामले में, सीधी रेखा और समतल में एक ही उभयनिष्ठ बिंदु होता है, जिसे सीधी रेखा और समतल का प्रतिच्छेदन बिंदु कहा जाता है। संक्षेप में लिखते समय, मैं प्रतिच्छेदन को "" चिन्ह से निरूपित करता हूँ। उदाहरण के लिए, संकेतन का अर्थ है कि सीधी रेखा बिंदु एम पर विमान को काटती है। जब एक समतल एक निश्चित सीधी रेखा को काटता है, तो सीधी रेखा और समतल के बीच एक कोण की अवधारणा उत्पन्न होती है।

अलग से, यह उस सीधी रेखा पर ध्यान देने योग्य है जो विमान को काटती है और इस विमान में पड़ी किसी भी सीधी रेखा के लंबवत है। ऐसी रेखा को समतल पर लंबवत कहा जाता है। लंबवतता को संक्षेप में रिकॉर्ड करने के लिए, प्रतीक "" का उपयोग करें। सामग्री के अधिक गहन अध्ययन के लिए, आप एक सीधी रेखा और एक तल की लंबवतता लेख का संदर्भ ले सकते हैं।

विमान से संबंधित समस्याओं को हल करते समय विमान के तथाकथित सामान्य वेक्टर का विशेष महत्व है। किसी समतल का सामान्य सदिश इस तल के लंबवत रेखा पर स्थित कोई भी गैर-शून्य सदिश होता है।

तीसरा, एक सीधी रेखा समतल के समानांतर हो सकती है, यानी इसमें उभयनिष्ठ बिंदु नहीं हो सकते हैं। संक्षेप में समवर्ती लिखते समय, प्रतीक "" का उपयोग करें। उदाहरण के लिए, यदि रेखा a समतल के समानांतर है, तो हम लिख सकते हैं। हम अनुशंसा करते हैं कि आप एक रेखा और एक तल की समानता लेख का हवाला देकर इस मामले का अधिक विस्तार से अध्ययन करें।

कहना चाहिए कि एक समतल में पड़ी एक सीधी रेखा इस समतल को दो अर्ध-तलों में विभाजित करती है। इस मामले में सीधी रेखा को अर्ध-तलों की सीमा कहा जाता है। एक ही अर्ध-तल के कोई भी दो बिंदु एक रेखा के एक ही तरफ स्थित होते हैं, और विभिन्न आधे-तल के दो बिंदु सीमा रेखा के विपरीत किनारों पर स्थित होते हैं।

विमानों की पारस्परिक व्यवस्था.

अंतरिक्ष में दो विमान संपाती हो सकते हैं। इस मामले में उनमें कम से कम तीन बिंदु समान हैं।

अंतरिक्ष में दो विमान एक दूसरे को काट सकते हैं। दो विमानों का प्रतिच्छेदन एक सीधी रेखा है, जो स्वयंसिद्ध द्वारा स्थापित की जाती है: यदि दो विमानों का एक सामान्य बिंदु है, तो उनके पास एक सामान्य सीधी रेखा है जिस पर इन विमानों के सभी सामान्य बिंदु स्थित हैं।

इस मामले में, प्रतिच्छेदी विमानों के बीच एक कोण की अवधारणा उत्पन्न होती है। विशेष रुचि वह स्थिति होती है जब तलों के बीच का कोण नब्बे डिग्री होता है। ऐसे विमानों को लंबवत कहा जाता है। हमने उनके बारे में विमानों की लंबवतता लेख में बात की थी।

अंततः, अंतरिक्ष में दो तल समानांतर हो सकते हैं, यानी उनका कोई उभयनिष्ठ बिंदु नहीं हो सकता। हम अनुशंसा करते हैं कि आप विमानों की सापेक्ष व्यवस्था के लिए इस विकल्प की पूरी समझ प्राप्त करने के लिए विमानों की समानता लेख पढ़ें।

समतल को परिभाषित करने की विधियाँ.

अब हम अंतरिक्ष में एक विशिष्ट विमान को परिभाषित करने के मुख्य तरीकों की सूची देंगे।

सबसे पहले, एक समतल को अंतरिक्ष में तीन बिंदु निर्धारित करके परिभाषित किया जा सकता है जो एक ही सीधी रेखा पर नहीं होते हैं। यह विधि स्वयंसिद्ध पर आधारित है: किन्हीं तीन बिंदुओं से होकर जो एक ही रेखा पर नहीं हैं, एक ही तल है।

यदि एक विमान को तीन अलग-अलग बिंदुओं के निर्देशांक को इंगित करके त्रि-आयामी अंतरिक्ष में तय और निर्दिष्ट किया जाता है जो एक ही सीधी रेखा पर नहीं होते हैं, तो हम दिए गए तीन बिंदुओं से गुजरने वाले विमान के समीकरण को लिख सकते हैं।

किसी समतल को परिभाषित करने की अगली दो विधियाँ पिछली विधि का परिणाम हैं। वे तीन बिंदुओं से गुजरने वाले विमान के बारे में स्वयंसिद्ध के परिणामों पर आधारित हैं:

• एक विमान एक रेखा और एक बिंदु से होकर गुजरता है जो उस पर नहीं है, और केवल एक (एक रेखा और एक बिंदु से गुजरने वाले विमान के समीकरण का लेख भी देखें);
• दो प्रतिच्छेदी रेखाओं से होकर गुजरने वाला केवल एक ही विमान है (हम अनुशंसा करते हैं कि आप लेख में दी गई सामग्री पढ़ें: दो प्रतिच्छेदी रेखाओं से गुजरने वाले एक विमान का समीकरण)।

अंतरिक्ष में किसी समतल को परिभाषित करने का चौथा तरीका समानांतर रेखाओं को परिभाषित करने पर आधारित है। याद रखें कि अंतरिक्ष में दो रेखाएँ समानांतर कहलाती हैं यदि वे एक ही तल में हों और प्रतिच्छेद न करें। इस प्रकार, अंतरिक्ष में दो समानांतर रेखाओं को इंगित करके, हम उस एकमात्र तल का निर्धारण करेंगे जिसमें ये रेखाएँ स्थित हैं।

यदि आयताकार समन्वय प्रणाली के सापेक्ष त्रि-आयामी अंतरिक्ष में संकेतित तरीके से एक विमान दिया गया है, तो हम दो समानांतर रेखाओं से गुजरने वाले विमान के लिए एक समीकरण बना सकते हैं।

हाई स्कूल ज्यामिति पाठों में, निम्नलिखित प्रमेय सिद्ध होता है: अंतरिक्ष में एक निश्चित बिंदु के माध्यम से एक दी गई रेखा पर लंबवत एक एकल विमान गुजरता है। इस प्रकार, हम एक विमान को परिभाषित कर सकते हैं यदि हम उस बिंदु को निर्दिष्ट करें जिससे वह गुजरता है और उस पर लंबवत एक रेखा निर्दिष्ट करें।

यदि एक आयताकार समन्वय प्रणाली त्रि-आयामी अंतरिक्ष में तय की जाती है और एक विमान को संकेतित तरीके से निर्दिष्ट किया जाता है, तो किसी दिए गए सीधी रेखा के लंबवत बिंदु से गुजरने वाले विमान के लिए एक समीकरण बनाना संभव है।

समतल पर लंबवत रेखा के बजाय, आप इस समतल के सामान्य सदिशों में से एक को निर्दिष्ट कर सकते हैं। ऐसे में लिखना संभव है