Construction of orthogonal projections of points. Projecting a point onto three projection planes Projecting a point onto a plane

When solving geometric problems in space, the problem of determining the distance between a plane and a point often arises. In some cases, this is necessary for a comprehensive solution. This value can be calculated by finding the projection onto the plane of the point. Let's consider this issue in more detail in the article.

Equation to describe a plane

Before proceeding to consider the question of how to find the projection of a point onto a plane, you should get acquainted with the types of equations that define the latter in three-dimensional space. More details below.

A general equation that defines all points that belong to a given plane is the following:

A*x + B*y + C*z + D = 0.

The first three coefficients are the coordinates of the vector, which is called the guide for the plane. It coincides with the normal for it, that is, it is perpendicular. This vector is denoted by n¯(A; B; C). The free coefficient D is uniquely determined from the knowledge of the coordinates of any point belonging to the plane.

The concept of the projection of a point and its calculation

Suppose that some point P(x 1 ; y 1 ; z 1) and a plane are given. It is defined by the equation in general form. If we draw a perpendicular line from P to a given plane, then it is obvious that it intersects the latter at one specific point Q (x 2 ; y 2 ​​; z 2). Q is called the projection of P onto the plane under consideration. The length of the segment PQ is called the distance from the point P to the plane. So PQ itself is perpendicular to the plane.

How can you find the coordinates of the projection of a point onto a plane? It is not difficult to do this. First you need to draw up an equation for a straight line that will be perpendicular to the plane. The point P will belong to it. Since the normal vector n¯(A; B; C) of this line must be parallel, the equation for it in the appropriate form can be written as follows:

(x; y; z) = (x 1 ; y 1 ; z 1) + λ*(A; B; C).

Where λ is a real number, which is usually called a parameter of the equation. By changing it, you can get any point of the line.

After the vector equation for a line perpendicular to the plane is written, it is necessary to find a common intersection point for the considered geometric objects. Its coordinates will be the projection P. Since they must satisfy both equalities (for the straight line and for the plane), the problem is reduced to solving the corresponding system of linear equations.

The concept of projection is often used in the study of drawings. They depict lateral and horizontal projections of the part on the zy, zx, and xy planes.

Calculating the distance from a plane to a point

As noted above, knowing the coordinates of the projection onto the plane of the point allows you to determine the distance between them. Using the notation introduced in the previous paragraph, we obtain that the desired distance is equal to the length of the segment PQ. To calculate it, it is enough to find the coordinates of the vector PQ¯, and then calculate its modulus using a well-known formula. The final expression for the distance d between the P point and the plane becomes:

d = |PQ¯| \u003d √ ((x 2 - x 1) 2 + (y 2 - y 1) 2 + (z 2 - z 1) 2).

The resulting value of d is presented in units in which the current Cartesian coordinate system xyz is specified.

Task example

Suppose there is a point N(0; -2; 3) and a plane, which is described by the following equation:

You should find the projection points on the plane and calculate the distance between them.

First of all, we will formulate the equation of a straight line that intersects the plane at an angle of 90 o. We have:

(x; y; z) = (0; -2; 3) + λ*(2; -1; 1).

Writing this equality explicitly, we arrive at the following system of equations:

Substituting the coordinate values ​​from the first three equalities into the fourth one, we obtain the value λ, which determines the coordinates of the common point of the line and the plane:

2*(2*λ) - (-2 - λ) + λ + 3 + 4 = 0 =>

6*λ + 9 = 0

λ = 9/6 = 3/2 = 1.5.

We substitute the found parameter in and find the coordinates of the projection of the starting point onto the plane:

(x; y; z) = (0; -2; 3) + 1.5*(2; -1; 1) = (3; -3.5; 4.5).

To calculate the distance between the geometric objects specified in the problem statement, we apply the formula for d:

d = √((3 - 0) 2 + (-3.5 + 2) 2 + (4.5 - 3) 2) = 3.674.

In this problem, we showed how to find the projection of a point onto an arbitrary plane and how to calculate the distance between them.

The position of a point in space can be specified by its two orthogonal projections, for example, horizontal and frontal, frontal and profile. The combination of any two orthogonal projections allows you to find out the value of all coordinates of a point, build a third projection, determine the octant in which it is located. Let's consider some typical tasks from the course of descriptive geometry.

According to the given complex drawing of points A and B, it is necessary:

Let us first determine the coordinates of point A, which can be written in the form A (x, y, z). The horizontal projection of point A is point A ", having coordinates x, y. Draw from point A" perpendiculars to the x, y axes and find, respectively, A x, A y. The x-coordinate for point A is equal to the length of the segment A x O with a plus sign, since A x lies in the region of positive x-axis values. Taking into account the scale of the drawing, we find x \u003d 10. The y coordinate is equal to the length of the segment A y O with a minus sign, since t. A y lies in the region of negative y-axis values. Given the scale of the drawing, y = -30. The frontal projection of point A - point A"" has x and z coordinates. Let's drop the perpendicular from A"" to the z-axis and find A z . The z-coordinate of point A is equal to the length of the segment A z O with a minus sign, since A z lies in the region of negative values ​​of the z-axis. Given the scale of the drawing, z = -10. Thus, the coordinates of point A are (10, -30, -10).

The coordinates of point B can be written as B (x, y, z). Consider the horizontal projection of point B - point B. "Since it lies on the x axis, then B x \u003d B" and the coordinate B y \u003d 0. The abscissa x of point B is equal to the length of the segment B x O with a plus sign. Taking into account the scale of the drawing, x = 30. The frontal projection of the point B - point B˝ has the coordinates x, z. Draw a perpendicular from B"" to the z-axis, thus finding B z . The applicate z of point B is equal to the length of the segment B z O with a minus sign, since B z lies in the region of negative values ​​of the z-axis. Taking into account the scale of the drawing, we determine the value z = -20. So the B coordinates are (30, 0, -20). All necessary constructions are shown in the figure below.

Construction of projections of points

Points A and B in the P 3 plane have the following coordinates: A""" (y, z); B""" (y, z). In this case, A"" and A""" lie on the same perpendicular to the z-axis, since they have a common z-coordinate. In the same way, B"" and B""" lie on a common perpendicular to the z-axis. To find the profile projection of t. A, we set aside along the y-axis the value of the corresponding coordinate found earlier. In the figure, this is done using an arc of a circle of radius A y O. After that, we draw a perpendicular from A y to the intersection with the perpendicular restored from the point A "" to the z axis. The intersection point of these two perpendiculars determines the position of A""".

Point B""" lies on the z-axis, since the y-ordinate of this point is equal to zero. To find the profile projection of point B in this problem, it is only necessary to draw a perpendicular from B"" to the z-axis. The point of intersection of this perpendicular with the z-axis is B """.

Determining the position of points in space

Visualizing the spatial layout, composed of the projection planes P 1, P 2 and P 3, the location of the octants, as well as the order of transformation of the layout into diagrams, you can directly determine that t. A is located in the III octant, and t. B lies in the plane P 2 .

Another option for solving this problem is the method of exceptions. For example, the coordinates of point A are (10, -30, -10). The positive abscissa x makes it possible to judge that the point is located in the first four octants. A negative y-ordinate indicates that the point is in the second or third octant. Finally, the negative applicate of z indicates that point A is in the third octant. The given reasoning is clearly illustrated by the following table.

Octants	Coordinate signs
	x	y	z
1	+	+	+
2	+	–	+
3	+	–	–
4	+	+	–
5	–	+	+
6	–	–	+
7	–	–	–
8	–	+	–

Point B coordinates (30, 0, -20). Since the ordinate of t. B is equal to zero, this point is located in the projection plane П 2 . The positive abscissa and the negative applicate of point B indicate that it is located on the border of the third and fourth octants.

Construction of a visual image of points in the system of planes P 1, P 2, P 3

Using the frontal isometric projection, we built a spatial layout of the third octant. It is a rectangular trihedron, whose faces are the planes P 1, P 2, P 3, and the angle (-y0x) is 45 º. In this system, segments along the x, y, z axes will be plotted in full size without distortion.

The construction of a visual image of point A (10, -30, -10) will begin with its horizontal projection A ". Having set aside the corresponding coordinates along the abscissa and ordinates, we find the points A x and A y. The intersection of perpendiculars restored from A x and A y respectively to the x and y axes determines the position of point A". Putting from A" parallel to the z axis towards its negative values ​​the segment AA", whose length is 10, we find the position of point A.

A visual image of point B (30, 0, -20) is constructed in a similar way - in the P 2 plane, the corresponding coordinates must be set aside along the x and z axes. The intersection of the perpendiculars reconstructed from B x and B z will determine the position of point B.

Projection apparatus

The projection apparatus (Fig. 1) includes three projection planes:

π 1 - horizontal projection plane;

π 2 - frontal projection plane;

π 3– profile plane of projections .

The projection planes are mutually perpendicular ( π 1^ π 2^ π 3), and their intersection lines form axes:

Plane intersection π 1 And π 2 form an axis 0X (π 1∩ π 2 = 0X);

Plane intersection π 1 And π 3 form an axis 0Y (π 1∩ π 3 = 0Y);

Plane intersection π 2 And π 3 form an axis 0Z (π 2∩ π 3 = 0Z).

The point of intersection of the axes (ОХ∩OY∩OZ=0) is considered to be the reference point (point 0).

Since the planes and axes are mutually perpendicular, such an apparatus is similar to the Cartesian coordinate system.

The projection planes divide the entire space into eight octants (in Fig. 1 they are indicated by Roman numerals). Projection planes are considered opaque, and the viewer is always in I th octane.

Projection orthogonal with projection centers S1, S2 And S3 respectively for the horizontal, frontal and profile projection planes.

A.

From projection centers S1, S2 And S3 projecting beams come out l 1, l 2 And l 3 A

- A 1 A;

- A 2– frontal projection of the point A;

- A 3– profile projection of a point A.

A point in space is characterized by its coordinates A(x,y,z). points A x, A y And Az respectively on the axes 0X, 0Y And 0Z show coordinates x, y And z points A. On fig. 1 gives all the necessary designations and shows the relationship between the point A space, its projections and coordinates.

point diagram

To plot a point A(Fig. 2), in the projection apparatus (Fig. 1) the plane π 1 A 1 0X π 2. Then the plane π 3 with point projection A 3, rotate counterclockwise around the axis 0Z, until it coincides with the plane π 2. Direction of rotation of planes π 2 And π 3 shown in fig. 1 arrows. At the same time, direct A 1 A x And A 2 A x 0X perpendicular A 1 A 2, and straight lines A 2 A x And A 3 A x will be located in common to the axis 0Z perpendicular A 2 A 3. These lines will be referred to as vertical And horizontal connection lines.

It should be noted that during the transition from the projection apparatus to the diagram, the projected object disappears, but all information about its shape, geometric dimensions and its position in space are preserved.

A(x A , y A , z Ax A , y A And z A in the following sequence (Fig. 2). This sequence is called the point plotting technique.

1. Axes are drawn orthogonally OX, OY And oz.

2. On the axis OX x A points A and get the position of the point A x.

3. Through the dot A x perpendicular to the axis OX

A x in the direction of the axis OY the numerical value of the coordinate is postponed y A points A A 1 on the plot.

A x in the direction of the axis oz the numerical value of the coordinate is postponed zA points A A 2 on the plot.

6. Through the dot A 2 parallel to axis OX a horizontal line is drawn. The intersection of this line and the axis oz will give the position of the point A z.

7. On a horizontal line from the point A z in the direction of the axis OY the numerical value of the coordinate is postponed y A points A and the position of the profile projection of the point is determined A 3 on the plot.

Point characteristic

All points of space are subdivided into points of private and general positions.

Private position points. Points belonging to the projection apparatus are called points of particular position. These include points belonging to the projection planes, axes, origin and projection centers. The characteristic features of points of private position are:

Metamathematical - one, two or all numerical values ​​of the coordinates are equal to zero and (or) infinity;

On the diagram - two or all projections of the point are located on the axes and (or) are located at infinity.

Points in general position. Points in general position include points that do not belong to the projection apparatus. For example, dot A in fig. 1 and 2.

In the general case, the numerical values ​​of the coordinates of a point characterize its distance from the projection plane: the coordinate X from the plane π 3; coordinate y from the plane π 2; coordinate z from the plane π 1. It should be noted that the signs at the numerical values ​​of the coordinates indicate the direction of removal of the point from the projection planes. Depending on the combination of signs for the numerical values ​​of the coordinates of the point, it depends in which of the octane it is located.

Two Image Method

In practice, in addition to the full projection method, the two-image method is used. It differs in that the third projection of the object is excluded in this method. To obtain a projection apparatus for the two-image method, the profile projection plane with its projection center is excluded from the full projection apparatus (Fig. 3). In addition, on the axis 0X the origin is assigned (point 0 ) and from it perpendicular to the axis 0X in projection planes π 1 And π 2 spend axis 0Y And 0Z respectively.

In this apparatus, the entire space is divided into four quadrants. On fig. 3 are marked with Roman numerals.

Projection planes are considered opaque, and the viewer is always in I th quadrant.

Consider the operation of the device using the example of projecting a point A.

From projection centers S1 And S2 projecting beams come out l 1 And l 2. These rays pass through the point A and intersecting with the projection planes form its projections:

- A 1- horizontal projection of a point A;

- A 2– frontal projection of the point A.

To plot a point A(Fig. 4), in the projection apparatus (Fig. 3) the plane π 1 with the resulting point projection A 1 rotate clockwise around an axis 0X, until it coincides with the plane π 2. Plane rotation direction π 1 shown in fig. 3 arrows. At the same time, only one point remains on the diagram of the point obtained by the two-image method. vertical communication line A 1 A 2.

In practice, plotting a point A(x A , y A , z A) is carried out according to the numerical values ​​of its coordinates x A , y A And z A in the following sequence (Fig. 4).

1. An axis is drawn OX and the origin is assigned (point 0 ).

2. On the axis OX the numerical value of the coordinate is postponed x A points A and get the position of the point A x.

3. Through the dot A x perpendicular to the axis OX a vertical line is drawn.

4. On the vertical line from the point A x in the direction of the axis OY the numerical value of the coordinate is postponed y A points A and the position of the horizontal projection of the point is determined A 1 OY is not plotted, but its positive values ​​are assumed to be below the axis OX, while the negative ones are higher.

5. On the vertical line from the point A x in the direction of the axis oz the numerical value of the coordinate is postponed zA points A and the position of the frontal projection of the point is determined A 2 on the plot. It should be noted that on the diagram the axis oz is not drawn, but it is assumed that its positive values ​​are located above the axis OX, while the negative ones are lower.

Competing points

Points on the same projecting ray are called competing points. They have a common projection in the direction of the projecting beam, i.e. their projections coincide identically. A characteristic feature of competing points on the diagram is the identical coincidence of their projections of the same name. The competition lies in the visibility of these projections relative to the observer. In other words, in space for the observer, one of the points is visible, the other is not. And, accordingly, in the drawing: one of the projections of competing points is visible, and the projection of the other point is invisible.

On a spatial projection model (Fig. 5) from two competing points A And IN visible dot A on two mutually complementary grounds. According to the chain S 1 →A→B dot A closer to the observer than a point IN. And, accordingly, further from the projection plane π 1(those. zA > zA).

Rice. 5 Fig.6

If the point itself is visible A, then its projection is also visible A 1. In relation to the projection coinciding with it B1. For clarity and, if necessary, on the diagram, invisible projections of points are usually enclosed in brackets.

Remove points on the model A And IN. Their coinciding projections on the plane will remain π 1 and separate projections - on π 2. We conditionally leave the frontal projection of the observer (⇩), located in the center of the projection S1. Then along the chain of images ⇩ → A2 → B2 it will be possible to judge that zA > zB and that the point itself is visible A and its projection A 1.

Similarly, consider the competing points WITH And D apparently relative to the plane π 2 . Since the common projecting beam of these points l 2 parallel to axis 0Y, then the sign of visibility of competing points WITH And D is determined by the inequality yC > yD. Therefore, the point D closed by a dot WITH and, accordingly, the projection of the point D2 will be covered by the projection of the point From 2 on surface π 2.

Let's consider how the visibility of competing points is determined in a complex drawing (Fig. 6).

According to matching projections A 1≡IN 1 the points themselves A And IN are on the same projecting beam parallel to the axis 0Z. So coordinates are to be compared zA And zB these points. To do this, we use the frontal projection plane with separate point images. In this case zA > zB. It follows from this that the projection is visible A 1.

points C And D in the complex drawing under consideration (Fig. 6) are also on the same projecting beam, but only parallel to the axis 0Y. Therefore, from a comparison yC > yD we conclude that the projection C 2 is visible.

General rule. Visibility for coinciding projections of competing points is determined by comparing the coordinates of these points in the direction of a common projecting beam. Visible is the projection of the point for which this coordinate is greater. In this case, the comparison of coordinates is carried out on the plane of projections with separate images of points.

A point, as a mathematical concept, has no dimensions. Obviously, if the object of projection is a zero-dimensional object, then it is meaningless to talk about its projection.

Fig.9 Fig.10

In geometry under a point, it is advisable to take a physical object that has linear dimensions. Conventionally, a ball with an infinitely small radius can be taken as a point. With this interpretation of the concept of a point, we can talk about its projections.

When constructing orthogonal projections of a point, one should be guided by the first invariant property of orthogonal projection: the orthogonal projection of a point is a point.

The position of a point in space is determined by three coordinates: X, Y, Z, showing the distances at which the point is removed from the projection planes. To determine these distances, it is enough to determine the meeting points of these lines with the projection planes and measure the corresponding values, which will indicate, respectively, the values ​​of the abscissa X, ordinates Y and appliques Z points (Fig. 10).

The projection of a point is the base of the perpendicular dropped from the point to the corresponding projection plane. Horizontal projection points A call the rectangular projection of a point on the horizontal plane of projections, frontal projection a /- respectively on the frontal plane of projections and profile a // – on the profile projection plane.

Direct Aa, Aa / And Aa // are called projecting lines. At the same time, direct Ah, projecting point A on the horizontal plane of projections, called horizontally projecting line, Аa / And Aa //- respectively: frontally And profile-projecting straight lines.

Two projecting lines passing through a point A define the plane, which is called projecting.

When converting the spatial layout, the frontal projection of the point A - a / remains in place as belonging to a plane that does not change its position under the considered transformation. Horizontal projection - A together with the horizontal projection plane will turn in the direction of clockwise movement and will be located on one perpendicular to the axis X with front projection. Profile projection - a // will rotate together with the profile plane and by the end of the transformation will take the position indicated in Figure 10. At the same time - a // will be perpendicular to the axis Z drawn from the point A / and will be removed from the axis Z the same distance as the horizontal projection A away from axis X. Therefore, the connection between the horizontal and profile projections of a point can be established using two orthogonal segments aa y And a y a // and a conjugating arc of a circle centered at the point of intersection of the axes ( ABOUT- origin). The marked connection is used to find the missing projection (for two given ones). The position of the profile (horizontal) projection according to the given horizontal (profile) and frontal projections can be found using a straight line drawn at an angle of 45 0 from the origin to the axis Y(this bisector is called a straight line) k is the Monge constant). The first of these methods is preferable, as it is more accurate.

Therefore:

1. Point in space removed:

from the horizontal plane H Z,

from the frontal plane V by the value of the given coordinate Y,

from profile plane W by the value of the coordinate. x.

2. Two projections of any point belong to the same perpendicular (one connection line):

horizontal and frontal - perpendicular to the axis x,

horizontal and profile - perpendicular to the Y axis,

frontal and profile - perpendicular to the Z axis.

3. The position of a point in space is completely determined by the position of its two orthogonal projections. Therefore - from any two given orthogonal projections of a point, it is always possible to construct its missing third projection.

If a point has three definite coordinates, then such a point is called point in general position. If a point has one or two coordinates equal to zero, then such a point is called private position point.

Rice. 11 Fig. 12

Figure 11 shows a spatial drawing of points of particular position, Figure 12 shows a complex drawing (diagrams) of these points. Dot A belongs to the frontal projection plane, the point IN– horizontal plane of projections, point WITH– profile plane of projections and point D– abscissa axis ( X).

Algebraic vector projection on any axis is equal to the product of the length of the vector and the cosine of the angle between the axis and the vector:

Right a b = |b|cos(a,b) or

Where a b is the scalar product of vectors , |a| - modulus of vector a .

Instruction. To find the projection of the vector Пp a b online, you must specify the coordinates of the vectors a and b . In this case, the vector can be given in the plane (two coordinates) and in space (three coordinates). The resulting solution is saved in a Word file. If the vectors are given through the coordinates of the points, then you must use this calculator.

Vector projection classification

Types of projections by definition vector projection

1. The geometric projection of the vector AB onto the axis (vector) is called the vector A"B", the beginning of which A’ is the projection of the beginning A onto the axis (vector), and the end B’ is the projection of the end B onto the same axis.
2. The algebraic projection of the vector AB onto the axis (vector) is called the length of the vector A"B" , taken with a + or - sign, depending on whether the vector A"B" has the same direction as the axis (vector).

Types of projections by coordinate system

Vector projection properties

1. The geometric projection of a vector is a vector (it has a direction).
2. The algebraic projection of a vector is a number.

Vector projection theorems

Theorem 1. The projection of the sum of vectors on any axis is equal to the projection of the terms of the vectors on the same axis.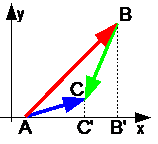

AC"=AB"+B"C"

Theorem 2. The algebraic projection of a vector onto any axis is equal to the product of the length of the vector and the cosine of the angle between the axis and the vector:

Pr a b = |b| cos(a,b)

Types of vector projections

1. projection onto the OX axis.
2. projection onto the OY axis.
3. projection onto a vector.

Projection onto the OX axis	Projection onto the OY axis	Projection to vector
If the direction of the vector A'B' coincides with the direction of the OX axis, then the projection of the vector A'B' has a positive sign.	If the direction of the vector A'B' coincides with the direction of the OY axis, then the projection of the vector A'B' has a positive sign.	If the direction of the vector A'B' coincides with the direction of the vector NM, then the projection of the vector A'B' has a positive sign.
If the direction of the vector is opposite to the direction of the OX axis, then the projection of the vector A'B' has a negative sign.	If the direction of the vector A'B' is opposite to the direction of the OY axis, then the projection of the vector A'B' has a negative sign.	If the direction of the vector A'B' is opposite to the direction of the vector NM, then the projection of the vector A'B' has a negative sign.
If the vector AB is parallel to the axis OX, then the projection of the vector A'B' is equal to the modulus of the vector AB.	If the vector AB is parallel to the OY axis, then the projection of the vector A'B' is equal to the modulus of the vector AB.	If the vector AB is parallel to the vector NM, then the projection of the vector A'B' is equal to the modulus of the vector AB.
If the vector AB is perpendicular to the axis OX, then the projection of A'B' is equal to zero (zero-vector).	If the vector AB is perpendicular to the OY axis, then the projection of A'B' is equal to zero (a null vector).	If the vector AB is perpendicular to the vector NM, then the projection of A'B' is equal to zero (a null vector).

1. Question: Can the projection of a vector have a negative sign. Answer: Yes, vector projections can be negative. In this case, the vector has the opposite direction (see how the OX axis and the AB vector are directed)
2. Question: Can the projection of a vector coincide with the modulus of the vector. Answer: Yes, it can. In this case, the vectors are parallel (or lie on the same line).
3. Question: Can the projection of a vector be equal to zero (zero-vector). Answer: Yes, it can. In this case, the vector is perpendicular to the corresponding axis (vector).

Example 1 . The vector (Fig. 1) forms an angle of 60 o with the OX axis (it is given by the vector a). If OE is a scale unit, then |b|=4, so .

Indeed, the length of the vector (geometric projection b) is equal to 2, and the direction coincides with the direction of the OX axis.

Example 2 . The vector (Fig. 2) forms an angle with the OX axis (with the vector a) (a,b) = 120 o . Length |b| vector b is equal to 4, so pr a b=4 cos120 o = -2.

Indeed, the length of the vector is equal to 2, and the direction is opposite to the direction of the axis.