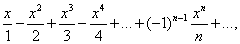
лухов Ю.П. Конспект лекций по высшей математике. Лекция № 42 5

Лекция 42

ТЕМА: Функциональные ряды

План.

1. Функциональные ряды. Область сходимости.
2. Равномерная сходимость. Признак Вейерштрасса.
3. Свойства равномерно сходящихся рядов: непрерывность суммы ряда, почленное интегрирование и дифференцирование.
4. Степенные ряды. Теорема Абеля. Область сходимости степенного ряда. Радиус сходимости.
5. Основные свойства степенных рядов: равномерная сходимость, непрерывность и бесконечная дифференцируемость суммы. Почленное интегрирование и дифференцирование степенных рядов.

Функциональные ряды. Область сходимости

Определение 40.1 . Бесконечная сумма функций

u 1 (x ) + u 2 (x ) +…+ u n (x ) +… , (40.1)

где u n (x ) = f (x , n ), называется функциональным рядом .

Если задать конкретное числовое значение х , ряд (40.1) превратится в числовой ряд, причем в зависимости от выбора значения х такой ряд может сходиться или расходиться. Практическую ценность представляют только сходящиеся ряды, поэтому важно определить те значения х , при которых функциональный ряд становится сходящимся числовым рядом.

Определение 40.2 . Множество значений х , при подстановке которых в функциональный ряд (40.1) получается сходящийся числовой ряд, называется областью сходимости функционального ряда.

Определение 40.3. Функция s (x ), определенная в области сходимости ряда, которая для каждого значения х из области сходимости равна сумме соответствующего числового ряда, полученного из (40.1) при данном значении х , называется суммой функционального ряда .

Пример. Найдем область сходимости и сумму функционального ряда

1 + х + х ² +…+ x n +…

При | x | ≥ 1 поэтому соответствующие числовые ряды расходятся. Если же

| x | < 1, рассматриваемый ряд представляет собой сумму бесконечно убывающей геометрической прогрессии, вычисляемую по формуле:

Следовательно, областью сходимости ряда является интервал (-1, 1), а его сумма имеет указанный вид.

Замечание . Так же, как для числовых рядов, можно ввести понятия частичной суммы функционального ряда:

s n = 1 + х + х ² +…+ x n

и остатка ряда: r n = s – s n .

Равномерная сходимость функционального ряда

Определим вначале понятие равномерной сходимости числовой последовательности.

Определение 40.4. Функциональная последовательность f n (x ) называется равномерно сходящейся к функции f на множестве Х , если и

Замечание 1. Будем обозначать обычную сходимость функциональной последователь-ности а равномерную сходимость - .

Замечание 2 . Отметим еще раз принципиальное отличие равномерной сходимости от обычной: в случае обычной сходимости при выбранном значении ε для каждого существует свой номер N , для которого при n > N выполняется неравенство:

При этом может оказаться, что подобрать для данного ε общий номер N , обеспечивающий выполнение этого неравенства для любого х , невозможно. В случае же равномерной сходимости такой номер N , общий для всех х , существует.

Определим теперь понятие равномерной сходимости функционального ряда. Поскольку каждому ряду соответствует последовательность его частичных сумм, равномерная сходимость ряда определяется через равномерную сходимость этой последовательности:

Определение 40.5. Функциональный ряд называется равномерно сходящимся на множестве Х , если на Х равномерно сходится последовательность его частичных сумм.

Признак Вейерштрасса

Теорема 40.1. Если числовой ряд сходится и для всех и для всех п = 1, 2,… выполняется неравенство то ряд сходится абсолютно и равномерно на множестве Х.

Доказательство.

Для любого ε > 0 c уществует такой номер N , что поэтому и

Для остатков r n ряда справедлива оценка

Следовательно, поэтому ряд равномерно сходится.

Замечание. Процедура подбора числового ряда, отвечающего условиям теоремы 40.1, обычно называется мажорированием , а сам этот ряд – мажорантой для данного функционального ряда.

Пример. Для функционального ряда мажорантой при любом значении х является сходящийся знакоположительный ряд. Поэтому исходный ряд равно-мерно сходится на (-∞, +∞).

Свойства равномерно сходящихся рядов

Теорема 40.2. Если функции u n (x ) непрерывны при и ряд равномерно сходится на Х , то его сумма s (x ) тоже непрерывна в точке х 0 .

Доказательство.

Выберем ε > 0. Тогда, поэтому существует такой номер п 0 , что

- сумма конечного числа непрерывных функций, поэтому непрерывна в точке х 0 . Поэтому существует такое δ > 0, что Тогда получаем:

То есть функция s (x ) непрерывна при х = х 0 .

Теорема 40.3. Пусть функции u n (x ) непрерывны на отрезке [ a , b ] и ряд равно-мерно сходится на этом отрезке. Тогда ряд тоже равномерно сходится на [ a , b ] и (40.2)

(то есть в условиях теоремы ряд можно почленно интегрировать).

Доказательство.

По теореме 40.2 функция s (x ) = непрерывна на [ a , b ] и, следовательно, интегрируема на нем, то есть интеграл, стоящий в левой части равенства (40.2), существует. Покажем, что ряд равномерно сходится к функции

Обозначим

Тогда для любого ε найдется такой номер N , что при n > N

Значит, ряд равномерно сходится, и его сумма равна σ (х ) = .

Теорема доказана.

Теорема 40.4. Пусть функции u n (x ) непрерывно дифференцируемы на отрезке [ a , b ] и ряд, составленный из их производных:

(40.3)

равномерно сходится на [ a , b ]. Тогда, если ряд сходится хотя бы в одной точке, то он сходится равномерно на всем [ a , b ], его сумма s (x )= является непрерывно дифференцируемой функцией и

(ряд можно почленно дифференцировать).

Доказательство.

Определим функцию σ(х ) как. По теореме 40.3 ряд (40.3) можно почленно интегрировать:

Ряд, стоящий в правой части этого равенства, равномерно сходится на [ a , b ] по теореме 40.3. Но числовой ряд по условию теоремы сходится, следовательно, равномерно сходится и ряд. Тогда Функция σ(t ) является суммой равномерно сходящегося ряда непрерывных функций на [ a , b ] и поэтому сама непрерывна. Тогда функция непрерывно дифференцируема на [ a , b ], и, что и требовалось доказать.

Определение 41.1 . Степенным рядом называется функциональный ряд вида

(41.1)

Замечание. С помощью замены х – х 0 = t ряд (41.1) можно привести к виду, поэтому все свойства степенных рядов достаточно доказать для рядов вида

(41.2)

Теорема 41.1 (1-я теорема Абеля). Если степенной ряд (41.2) сходится при х = х 0 , то при любом x : | x | < | x 0 | ряд (41.2) сходится абсолютно. Если же ряд (41.2) расходится при х = х 0 , то он расходится при любом x : | x | > | x 0 |.

Доказательство.

Если ряд сходится, то поэтому существует константа с > 0:

Следовательно, а ряд при | x |<| x 0 | сходится, так как является суммой бесконечно убывающей геометрической прогрессии. Значит, ряд при | x |<| x 0 | абсолютно сходится.

Если известно, что ряд (41.2) расходится при х = х 0 , то он не может сходиться при | x | > | x 0 | , так как из ранее доказанного при этом следовало бы, что он сходится и в точке х 0 .

Таким образом, если найти наибольшее из чисел х 0 > 0 таких, что (41.2) сходится при х = х 0 , то областью сходимости данного ряда, как следует из теоремы Абеля, будет интервал (- х 0 , х 0 ), возможно, включающий одну или обе границы.

Определение 41.2. Число R ≥ 0 называется радиусом сходимости степенного ряда (41.2), если этот ряд сходится, а расходится. Интервал (- R , R ) называется интервалом сходимости ряда (41.2).

Примеры.

1. Для исследования абсолютной сходимости ряда применим признак Даламбера: . Следовательно, ряд сходится только при х = 0, и радиус его сходимости равен 0: R = 0.
2. Используя тот же признак Даламбера, можно показать, что ряд сходится при любом х , то есть
3. Для ряда по признаку Даламбера получим:

Следовательно, при –1 < x < 1 ряд сходится, при

x < -1 и x > 1 расходится. При х = 1 получаем гармонический ряд, который, как извест-но, расходится, а при х = -1 ряд сходится условно по признаку Лейбница. Таким образом, радиус сходимости рассматриваемого ряда R = 1, а интервал сходи-мости – [-1, 1).

Формулы для определения радиуса сходимости степенного ряда.

1. Формула Даламбера.

Рассмотрим степенной ряд и применим к нему признак Даламбера: для сходимости ряда необходимо, чтобы.Если существует, то область сходимости определяется неравенством, то есть

- (41.3)

• формула Даламбера для вычисления радиуса сходимости.

1. Формула Коши-Адамара.

Используя радикальный признак Коши и рассуждая аналогичным образом, получим, что можно задать область сходимости степенного ряда как множество решений неравенства при условии существования этого предела, и, соответствен-но, найти еще одну формулу для радиуса сходимости:

(41.4)

• формула Коши-Адамара .

Свойства степенных рядов.

Теорема 41.2 (2-я теорема Абеля). Если R – радиус сходимости ряда (41.2) и этот ряд сходится при x = R , то он равномерно сходится на интервале (- R , R ).

Доказательство.

Знакоположительный ряд сходится по теореме 41.1. Следовательно, ряд (41.2) равномерно сходится в интервале [-ρ, ρ] по теореме 40.1. Из выбора ρ следует, что интервал равномерной сходимости – (- R , R ), что и требовалось доказать.

Следствие 1 . На всяком отрезке, целиком лежащем внутри интервала сходимости, сумма ряда (41.2) есть непрерывная функция.

Доказательство.

Члены ряда (41.2) являются непрерывными функциями, и ряд равномерно сходится на рассматриваемом отрезке. Тогда непрерывность его суммы следует из теоремы 40.2.

Следствие 2. Если пределы интегрирования α, β лежат внутри интервала сходимости степенного ряда, то интеграл от суммы ряда равен сумме интегралов от членов ряда:

(41.5)

Доказательство этого утверждения следует из теоремы 40.3.

Теорема 41.3. Если ряд (41.2) имеет интервал сходимости (- R , R ), то ряд

φ (x) = a 1 + 2 a 2 x + 3 a 3 x ² +…+ na n x n- 1 +…, (41.6)

полученный почленным дифференцированием ряда (41.2), имеет тот же интервал сходимости (- R , R ). При этом

φ΄(х) = s΄ (x ) при | x | < R , (41.7)

то есть внутри интервала сходимости производная от суммы степенного ряда равна сумме ряда, полученного его почленным дифференцированием.

Доказательство.

Выберем ρ: 0 < ρ < R и ζ: ρ < ζ < R . Тогда ряд сходится, следовательно, то есть Если | x | ≤ ρ, то

Где Таким образом, члены ряда (41.6) по модулю меньше членов знакоположительного ряда, который сходится по признаку Даламбера:

то есть является мажорантой для ряда (41.6) при Поэтому ряд (41.6) равно-мерно сходится на [-ρ, ρ]. Следовательно, по теореме 40.4 верно равенство (41.7). Из выбора ρ следует, что ряд (41.6) сходится в любой внутренней точке интервала (- R , R ).

Докажем, что вне этого интервала ряд (41.6) расходится. Действительно, если бы он сходился при x 1 > R , то, интегрируя его почленно на интервале (0, x 2 ), R < x 2 < x 1 , мы получили бы, что ряд (41.2) сходится в точке х 2 , что противоречит условию теоремы. Итак, теорема полностью доказана.

Замечание . Ряд (41.6) можно, в свою очередь, почленно дифференцировать и проделывать эту операцию сколько угодно раз.

Вывод: если степенной ряд сходится на интервале (- R , R ), то его сумма представляет собой функцию, имеющую внутри интервала сходимости производные любого порядка, каждая из которых есть сумма ряда, полученного из исходного с помощью почленного дифференцирования соответствующее количество раз; при этом интервал сходимости для ряда из производных любого порядка есть (- R , R ).

Кафедра информатики и высшей математики КГПУ

Функциональным рядом называется формально записанное выражение

u 1 (x ) + u 2 (x ) + u 3 (x ) + ... + u n (x ) + ... , (1)

где u 1 (x ), u 2 (x ), u 3 (x ), ..., u n (x ), ... - последовательность функций от независимой переменной x .

Сокращённая запись функционального ряда с сигмой: .

Примерами функциональных рядов могут служить :

(2)

(3)

Придавая независимой переменной x некоторое значение x 0 и подставляя его в функциональный ряд (1), получим числовой ряд

u 1 (x 0 ) + u 2 (x 0 ) + u 3 (x 0 ) + ... + u n (x 0 ) + ...

Если полученный числовой ряд сходится, то говорят, что функциональный ряд (1) сходится при x = x 0 ; если он расходится, что говорят, что ряд (1) расходится при x = x 0 .

Пример 1. Исследовать сходимость функционального ряда (2) при значениях x = 1 и x = - 1 .
Решение. При x = 1 получим числовой ряд

который сходится по признаку Лейбница. При x = - 1 получим числовой ряд

,

который расходится как произведение расходящегося гармонического ряда на – 1. Итак, ряд (2) сходится при x = 1 и расходится при x = - 1 .

Если такую проверку на сходимость функционального ряда (1) осуществить относительно всех значений независимой переменной из области определения его членов, то точки этой области разобьются на два множества: при значениях x , взятых в одном из них, ряд (1) сходится, а в другом – расходится.

Множество значений независимой переменной, при которых функциональный ряд сходится, называется его областью сходимости .

Пример 2. Найти область сходимости функционального ряда

Решение. Члены ряда определены на всей числовой прямой и образуют геометрическую прогрессию со знаменателем q = sin x . Поэтому ряд сходится, если

и расходится, если

(значения невозможны). Но при значениях и при остальных значениях x . Следовательно, ряд сходится при всех значениях x , кроме . Областью его сходимости служит вся числовая прямая, за исключением этих точек.

Пример 3. Найти область сходимости функционального ряда

Решение. Члены ряда образуют геометрическую прогрессию со знаменателем q =lnx . Поэтому ряд сходится, если , или , откуда . Это и есть область сходимости данного ряда.

Пример 4. Исследовать сходимость функционального ряда

Решение. Возьмём произвольное значение . При этом значении получим числовой ряд

(*)

Найдём предел его общего члена

Следовательно, ряд (*) расходится при произвольно выбранном, т.е. при любом значении x . Область его сходимости – пустое множество.

Равномерная сходимость функционального ряда и её свойства

Перейдём к понятию равномерной сходимости функционального ряда . Пусть s (x ) - сумма этого ряда, а s n (x ) - сумма n первых членов этого ряда. Функциональный ряд u 1 (x ) + u 2 (x ) + u 3 (x ) + ... + u n (x ) + ... называется равномерно сходящимся на отрезке [a , b ] , если для любого как угодно малого числа ε > 0 найдётся такой номер N , что при всех n ≥ N будет выполнятся неравенство

|s (x ) − s n (x )| < ε

для любого x из отрезка [a , b ] .

Приведённое выше свойство можно геометрически иллюстрировать следующим образом.

Рассмотрим график функции y = s (x ) . Построим около этой кривой полосу шириной 2ε n , то есть построим кривые y = s (x ) + ε n и y = s (x ) − ε n (на рисунке ниже они зелёного цвета).

Тогда при любом ε n график функции s n (x ) будет лежать целиком в рассматриваемой полосе. В этой же полосе будут лежать графики всех последующих частичных сумм.

Всякий сходящийся функциональный ряд, который не обладает описанным выше признаком - неравномерно сходящийся.

Рассмотрим ещё одно свойство равномерно сходящихся функциональых рядов:

сумма ряда непрерывных функций, равномерно сходящегося на некотором отрезке [a , b ] , есть функция, непрерывная на этом отрезке .

Пример 5. Определить, непрерывна ли сумма функционального ряда

Решение. Найдём сумму n первых членов этого ряда:

Если x > 0 , то

,

если x < 0 , то

если x = 0 , то

И поэтому .

Наше исследование показало, что сумма данного ряда - разрывная функция. Её график изображён на рисунке ниже.

Признак Вейерштрасса равномерной сходимости функциональных рядов

К признаку Вейерштрасса подойдём через понятие мажоририуемости функциональных рядов . Функциональный ряд

u 1 (x ) + u 2 (x ) + u 3 (x ) + ... + u n (x ) + ...

Область сходимости Функциональным рядом называется ряд членами которого являются функции / определенные на некотором множестве Е числовой оси. Например, члены ряда определены на интервале, а члены ряда определены на отрезке Функциональный ряд (1) называется сходящимся в точке Хо € Е, если сходится ФУНКЦИОНАЛЬНЫЕ РЯДЫ Область сходимости Равномерная сходимость Признак Вейерштрасса Свойства равномерно сходящихся функциональных рядов числовой ряд Если ряд (1) сходится в каждой точке х множества D С Е и расходится в каждой точке, множеству D не принадлежащей, то говорят, что ряд сходится на множестве D, и называют D областью сходимости ряда. Ряд (1) называется абсолютно сходящимся на множестве D, если на этом множестве сходится ряд В случае сходимости ряда (1) на множестве D его сумма S будет являться функцией, определенной на D, Область сходимости некоторых функциональных рядов можно найти с помощью известных достаточных признаков, установленных для рядов с положительными членами, например, признака Дапамбера, признака Коши. Пример 1. Найти область сходимости ряда М Так как числовой ряд сходится при р > 1 и расходится при р ^ 1, то, полагая р - Igx, получим данный ряд. который будет сходиться при Igx > Ц т.е. если х > 10, и расходиться при Igx ^ 1, т.е. при 0 < х ^ 10. Таким образом, областью сходимости ряда является луч Пример 2. Найти область сходимости ряда 4 Рассмотрим ряд Члены этого ряда положительны при всех значениях х. Применим к нему признак Даламбера. Имеем пе При ех < 1. т.е. при, этот ряд будет сходиться. Следовательно, заданный ряд сходится абсолютно на интервале При х > 0 ряд расходится, так как Л =. Расходимость ряда при х = 0 очевидна. Пример 3. Нейти область сходимости ряда Члены данного ряда определены и непрерывны на множестве. Применяя признак Кош и, найдем для любого. Следовательно, ряд расходится при всех значениях х. Обозначим через Sn(x) n-ю частичную сумму функционального ряда (1). Если этот ряд сходится на множестве D и его сумма равна 5(ж), то ее можно представить в виде где есть сумма сходящегося на множестве D ряда который называется п-м остатком функционального ряда (1). Для всех значений х € D имеет место соотношение и поэтому. т. е. остаток Rn(x) сходящегося ряда стремится к нулю при п оо, каково бы ни было х 6 D. Равномерная сходимость Среди всех сходящихся функциональных рядов важную роль играют так называемые равномерно сходящиеся ряды. Пусть дан сходящийся на множестве D функциональный ряд сумма которого равна S(x). Возьмем его n-ю частичную сумму Определение. Функциональный ряд ФУНКЦИОНАЛЬНЫЕ РЯДЫ Область сходимости Равномерная сходимость Признак Вейерштрасса Свойства равномерно сходящихся функциональных рядов называется равномерно сходящимся на множестве ПС1), если для любого числа е > О найдется число ЛГ > О такое, что неравенство будет выполняться для всех номеров п > N и для всех х из множества fI. Замечание. Здесь число N является одним и тем же для всех х € Ю, т.е. не зависит от z, однако зависит от выбора числа е, так что пишут N = N(e). Равномерную сходимость функционального ряда £ /п(®) к функции 5(х) на множестве ft часто обозначают так: Определение равномерной сходимости ряда /п(ж) на множестве ft можно за- писать короче с помощью логических символов: Поясним геометрически смысл равномерной сходимости функционального ряда. Возьмем в качестве множества ft отрезок [а, 6] и построим графики функций. Неравенство |, выполняющееся для номеров п> N и для всех a; G [а, Ь], можно записать в следующем виде Полученные неравенства показывают, что графики всех функций у = 5„(ж) с номерами п > N будут целиком заключены внутри £-полосы, ограниченной кривыми у = S(x) - е и у = 5(ж) + е (рис. 1). Пример 1 равномерно сходится на отрезке Данный ряд является знакочередующимся, удовлетворяет условиям признака Лейбница при всяком х € [-1,1] и, следовательно, сходится на отрезке (-1,1]. Пусть S(x) - его сумма, a Sn(x) - его п-я частичная сумма. Остаток ряда по абсолютной величине не превосходит абсолютной величины своего первого члена: а поскольку Возьмем любое е. Тогда неравенство | будет выполняться, если. Отсюда находим, что п > \. Если взять число (здесь через [а] обозначено наибольшее целое число, не превосходящее а), то неравенство | е будет выполняться для всех номеров п > N и для всех х € [-1,1). Это означает, что данный ряд равномерно сходится на отрезке [-1,1). I. Не всякий сходящийся на множестве D функциональный ряд является равномерно сходящимся на Пример 2. Покажем, что ряд сходится на отрезке, но не равномерно. 4 Вычислим п-ю частичную сумму £„(*) ряда. Имеем Откуда Данный ряд сходится на отрезке и его сумма если Абсолютная величина разности S(x) - 5„(х) (остатка ряда) равна. Возьмем число е такое, что. Пусть Разрешим неравенство относительно п. Имеем, откуда (так как, и при делении на Inx знак неравенства меняется на обратный). Неравенство будет выполняться при. Поэтому такого не зависящего от х числа N(e), чтобы неравенство выполнялось для каждого) сразу для всех х из отрезка. , не существует. Если же заменить отрезок 0 меньшим отрезком, где, то на последнем данный ряд будет сходиться к функции S0 равномерно. В самом деле, при, и поэтому при сразу для всех х §3. Признак Вейерштрасса Достаточный признак равномерной сходимости функционального ряда дается теоремой Вейерштрасса. Теорема 1 (признак Вейерштрасса). Пусть для всех х из множества Q члены функционального ряда по абсолютной величине не превосходят соответствующих членов сходящегося числового ряда П=1 с положительными членами, т. е. для всех х € Q. Тогда функциональный ряд (1) на множестве П сходится абсолютно и равномерно. А Тек как по условию теоремы члены ряда (1) удовлетворяют условию (3) на всем множестве Q, то по признаку сравнения ряд 2 \fn(x)\ сходится при любом х € И, и, следовательно, ряд (1) сходится на П абсолютно. Докажем равномерную сходимость ряда (1). Пусть Обозначим через Sn(x) и an частичные суммы рядов (1) и (2) соответственно. Имеем Возьмем любое (сколь угодно малое) число е > 0. Тогда из сходимости числового ряда (2) следует существование номера N = N(e) такого, что следовательно, -е для всех номеров п > N(e) и для всех хбП, т.е. ряд (1) сходится равномерно на множестве П. Замечание. Числовой ряд (2) часто называют мажорирующим, или мажорантным, для функционального ряда (1). Пример 1. Исследовать на равномерную сходимость ряд Неравенство выполняется для всех. и для всех. Числовой ряд сходится. В силу признака Вейерштрасса рассматриваемый функциональный ряд сходится абсолютно и равномерно на всей оси. Пример 2. Исследовать на равномерную сходимость ряд Члены ряда определены и непрерывны на отрезке [-2,2|. Так как на отрезке [-2,2) для любого натурального п, то Таким образом, неравенство выполняется для. Так как числовой ряд сходится, то по признаку Вейерштрасса исходный функциональный ряд сходится абсолютно и равномерно на отрезке. Замечание. Функциональный ряд (1) может сходится равномерно на множестве Пив том случае, когда не существует числового мажорантного ряда (2), т. е. признак Вейерштрасса яапяется лишь достаточным признаком для равномерной сходимости, но не является необходимым. Пример. Как было показано выше (пример), ряд равномерно сходится на отрезке 1-1,1]. Однако для него мажорантного сходящегося числового ряда (2) не существует. В самом деле, для всех натуральных п и для всех х € [-1,1) выполняется неравенство причем равенство достигается при. Поэтому члены искомого мажорантного ряда (2) непременно должны удовлетворять условию но числовой ряд ФУНКЦИОНАЛЬНЫЕ РЯДЫ Область сходимости Равномерная сходимость Признак Вейерштрасса Свойства равномерно сходящихся функциональных рядов расходится. Значит, будет расходиться и ряд £ оп. Свойства равномерно сходящихся функциональных рядов Равномерно сходящиеся функциональные ряды обладают рядом важных свойств. Теорема 2. Если все члены ряда равномерно сходящегося на отрезке [а, Ь], умножить на одну и ту же функцию д(х), ограниченную на [а, 6], то полученный функциональный ряд будет равномерно сходиться на. Пусть на отрезке [а, Ь\ ряд £ fn(x) равномерно сходится к функции 5(ж), а функ- ция д(х) ограничена, т. е. существует постоянная С > 0 такая, что По определению равномерной сходимости ряда для любого числа е > 0 существует номер N такой, что для всех п > N и для всех х € [а, Ь] будет выполняться неравенство где 5n(ar) - частичная сумма рассматриваемого ряда. Поэтому будем иметь и для любого. ряд равномерно сходится на [а, Ь| к функции Теорема 3. Пусть все члены fn(x) функционального ряда непрерывны и ряд сходится равномерно на отрезке [а, Ь\. Тогда сумма S(x) ряда непрерывна на этом отрезке. М Возьмем на отрезке [о, Ь] две произвольные точки гиг + Ах. Так как данный ряд сходится на отрезке [а, Ь] равномерно, то для любого числа е > О найдется номер N = N(e) такой, что для всех я > N будут выполняться неравенства где5„(ж) - частичные суммы ряда fn{x). Эти частичные суммы 5„(ж) непрерывны на отрезке [а, 6] как суммы конечного числа непрерывных на [а, 6) функций fn(x). Поэтому для фиксированного номера no > N(e) и взятого числа е найдется число 6 = 6(e) > 0 такое, что для приращения Ах, удовлетворяющего условию |, будет иметь место неравенство Приращение AS суммы S(x) можно представить в следующем виде: откуда. Учитывая неравенства (1) и (2), для приращений Ах, удовлетворяющих условию |, получим Это означает, что сумма Six) непрерывна в точке х. Так как х является произвольной точкой отрезка [а, 6], то 5(ж) непрерывна на |а, 6|. Замечание. Функциональный ряд члены которого непрерывны на отрезке [а, 6), но который сходится на (а, 6] неравномерно, может иметь суммой разрывную функцию. Пример 1. Рассмотрим функциональный ряд на отрезке |0,1). Вычислим его n-ю частичную сумму Поэтому Она разрывна на отрезке , хотя члены ряда непрерывны на нем. В силу доказанной теоремы данный ряд не является равномерно сходящимся на отрезке . Пример 2. Рассмотрим ряд Как было показано выше, этот ряд сходится при, ряд будет сходиться равномерно по признаку Вейерштрасса, так как 1 и числовой ряд сходится. Следовательно, для любого х > 1 сумма этого ряда непрерывна. Замечание. Функция называется функцией Рима на (эта функция играет большую роль в теории чисел). Теорема 4 (о почленном интегрировании функционального ряда). Пусть все члены fn(x) ряда непрерывны, и ряд сходится равномерно на отрезке [а, Ь] к функции S(x). Тогда справедливо равенство В силу непрерывности функций f„(x) и равномерной сходимости данного ряда на отрезке [а, 6] его сумма 5(ж) непрерывна и, следовательно, интегрируема на . Рассмотрим разность Из равномерной сходимости ряда на [о, Ь] следует, что для любого е > 0 найдется число N(e) > 0 такое, что для всех номеров п > N(e) и для всех х € [а, 6] будет выполняться неравенство Если ряд fn(0 не является равномерно сходящимся, то его, вообще говоря, нельзя почленно интегрировать, т. е. Теорема 5 (о почленном дифференцировании функционального ряда). Пусть все члены сходящегося ряда 00 имеют непрерывные производные и ряд составленный из этих производных, равномерно сходится на отрезке [а, Ь]. Тогда в любой точке справедливо равенство т. е. данный ряд можно почленно дифференцировать. М Положим Возьмем две любые точки. Тогда в силу теоремы 4 будем иметь Функция o-(x) непрерывна как сумма равномерно сходящегося ряда непрерывных функций. Поэтому, дифференцируя равенство получим Упражнения Найдите области сходимости данных функциональных рядов: Пользуясь признаком Вейерштрасса, докажите равномерную сходимость данных функциональных рядов на указанных интервалах:

Тема 2. Функциональные ряды. Степенные ряды

2.1. Функциональные ряды

До сих пор мы рассматривали ряды, членами которых были числа. Перейдем теперь к изучению рядов, членами которых являются функции.

Функциональным рядом называется ряд

членами которого являются функции одного и того же аргумента, определенные на одном множестве Е.

Например,

1.
;

2.
;

Если придать аргументу х некоторое числовое значение
,
, то получим числовой ряд

который может сходиться (сходиться абсолютно) или расходиться.

Если при
полученный числовой ряд сходится, то точка
называется точкой сходимости функционального ряда. Совокупность всех точек сходимости называется областью сходимости функционального ряда. Обозначим область сходимости Х , очевидно,
.

Если для числовых знакоположительных рядов ставится вопрос: «Сходится ряд или расходится?», для знакопеременных – вопрос: «Сходится как – условно или абсолютно,– или расходится?», то для функционального ряда основной вопрос звучит так: «Сходится (сходится абсолютно) при каких х ?».

Функциональный ряд
устанавливает закон, по которому каждому значению аргумента
,
, ставится в соответствие число, равное сумме числового ряда
. Таким образом, на множестве Х задается функция
, которая называется суммой функционального ряда .

Пример 16.

Найти область сходимости функционального ряда

.

Решение.

Пусть х – фиксированное число, тогда данный ряд можно рассматривать как числовой ряд, знакоположительный при
и знакопеременный при
.

Составим ряд из абсолютных величин членов данного ряда:

т.е для любого значения х этот предел меньше единицы, значит данный ряд сходится, причем абсолютно (так как исследовали ряд из абсолютных величин членов ряда) на всей числовой оси.

Таким образом, областью абсолютной сходимости является множество
.

Пример 17.

Найти область сходимости функционального ряда
.

Решение.

Пусть х – фиксированное число,
, тогда данный ряд можно рассматривать, как числовой ряд, знакоположительный при
и знакопеременный при
.

Рассмотрим ряд из абсолютных величин членов данного ряда:

и применим к нему признак ДАламбера.

По признаку ДАламбера ряд сходится, если величина предела меньше единицы, т.е. данный ряд будет сходиться, если
.

Решив это неравенство, получим:


.

Таким образом, при , ряд, составленный из абсолютных величин членов данного ряда, сходится, значит, исходный ряд сходится абсолютно, а при
данный ряд расходится.

При
ряд может сходится или расходится, так как при этих значениях х величина предела равна единицы. Поэтому дополнительно исследуем сходимость ряда точках
и
.

Подставляя в данный ряд
, получим числовой ряд
, про который известно, что он является гармоническим расходящимся рядом, значит, точка
– точка расходимости заданного ряда.

При
получается знакочередующийся числовой ряд

про который известно, что он сходится условно (смотри пример 15), значит, точка
– точка условной сходимости ряда.

Таким образом, область сходимости данного ряда , причем ряд сходится абсолютно при .

Функциональный ряд

называется мажорируемым в некоторой области изменения х, если существует такой сходящийся знакоположительный ряд

,

что для всех х из данной области выполняется условие
при
. Ряд
называется мажорантой.

Иначе говоря, ряд является мажорируемым, если каждый его член по абсолютной величине не больше соответствующего члена некоторого сходящегося знакоположительного ряда.

Например, ряд

является мажорируемым для любого х , так как для всех х выполняется соотношение

при
,

а ряд , как известно, является сходящимся.

Теорема Вейерштрасса

Ряд, мажорируемый в некоторой области, абсолютно сходится в этой области.

Рассмотрим для примера функциональный ряд
. Этот ряд является мажорируемым при
, так как при
члены ряда не превосходят соответствующих членов знакоположительного ряда . Следовательно, по теореме Вейерштрасса, рассмотренный функциональный ряд абсолютно сходится при
.

2.2. Степенной ряд. Теорема Абеля. Область сходимости степенного ряда

Среди всего многообразия функциональных рядов наиболее важными с точки зрения практического применения являются степенные и тригонометрические ряды. Рассмотрим такие ряды подробнее.

Степенным рядом по степеням
называется функциональный ряд вида

где – некоторое фиксированное число,
– числа, называемые коэффициентами ряда.

При
получаем степенной ряд по степеням х , который имеет вид

.

Для простоты будем рассматривать степенные ряды по степеням х , так как из такого ряда легко получить ряд по степеням
, подставив вместо х выражение
.

Простота и важность класса степенных рядов обусловлены в первую очередь тем, что частичная сумма степенного ряда

является многочленом – функцией, свойства которой хорошо изучены и значения которой легко вычисляются с помощью только арифметический операций.

Поскольку степенные ряды являются частным случаем функционального ряда, то для них так же необходимо находить область сходимости. В отличие от области сходимости произвольного функционального ряда, которая может быть множеством произвольного вида, область сходимости степенного ряда имеет вполне определенный вид. Об этом говорит следующая теорема.

Теорема Абеля.

Если степенной ряд
сходится при некотором значении
, то он сходится, причем абсолютно, при всех значениях х, удовлетворяющих условию
. Если степенной ряд расходится при некотором значении
, то он расходится и при значения, удовлетворяющих условию
.

Из теоремы Абеля следует, что все точки сходимости степенного ряда по степеням х расположены от начала координат не далее, чем любая из точек расходимости. Очевидно, что точки сходимости заполняют некоторый промежуток с центром в начале координат. справедлива теорема об области сходимости степенного ряда.

Теорема.

Для всякого степенного ряда
существует число R (R >0) такое, что при всех х, лежащих внутри интервала
, ряд сходится абсолютно и при всех х, лежащих вне интервала
, ряд расходится.

Число R называется радиусом сходимости степенного ряда, а интервал
– интервалом сходимости степенного ряда по степеням х.

Заметим, что в теореме ничего не говорится о сходимости ряда на концах интервала сходимости, т.е. в точках
. В этих точках различные степенные ряды ведут себя по-разному: ряд может сходиться (абсолютно или условно), а может расходиться. Поэтому сходимость ряда в этих точках следует проверять непосредственно по определению.

В частных случаях радиус сходимости ряда может быть равен нулю или бесконечности. Если
, то степенной ряд по степеням х сходится лишь в одной точке
; если же
, то степенной ряд сходится на всей числовой оси.

Еще раз обратим внимание на то, что степенной ряд
по степеням
может быть сведен к степенному ряду
с помощью замены
. Если ряд
сходится при
, т.е. для
, то после обратной замены получим

 или
.

Таким образом, интервал сходимости степенного ряда
имеет вид
. Точку называют центром сходимости . Для наглядности принято интервал сходимости изображать на числовой оси (рисунок 1)

Таким образом, область сходимости состоит из интервала сходимости, к которому могут быть добавлены точки
, если в этих точках ряд сходится. Интервал сходимости можно находить, применяя непосредственно признак ДАламбера или радикальный признак Коши к ряду, составленному из абсолютных величин членов данного ряда.

Пример 18.

Найти область сходимости ряда
.

Решение.

Данный ряд является степенным рядом по степеням х , т.е.
. Рассмотрим ряд, составленный из абсолютных величин членов данного ряда, и воспользуемся признаком ДАламбера.

Ряд будет сходиться, если величина предела меньше 1, т.е.

, откуда
.

Таким образом, интервал сходимости данного ряда
, радиус сходимости
.

Исследуем сходимость ряда на концах интервала, в точках
. Подставляя в данный ряд значение
, получим ряд

.

Полученный ряд является гармоническим расходящимся рядом, следовательно, в точке
ряд расходится, значит, точка
не входит в область сходимости.

При
получим знакочередующийся ряд

,

который является условно сходящимся (пример 15), следовательно, точка
– точка сходимости (условной).

Таким образом, область сходимости ряда
, причем в точке
ряд сходится условно, а в остальных точках - абсолютно.

Рассуждениям, использованным при решении примера, можно придать общий характер.

Рассмотрим степенной ряд

Составим ряд из абсолютных величин членов ряда и применим к нему признак Д"Аламбера.

Если существует (конечный или бесконечный) предел, то по условию сходимости признака Д"Аламбера ряд будет сходиться, если

,

,

.

Отсюда из определения интервала и радиуса сходимости имеем

Применяя радикальный признак Коши и рассуждая аналогично, можно получить еще одну формулу для нахождения радиуса сходимости

Пример 19

Решение.

Ряд является степенным по степеням х. Для нахождения интервала сходимости вычислим радиус сходимости по приведенной выше формуле. Для данного ряда формула числового коэффициента имеет вид

, тогда

Следовательно,

Так как R = , то ряд сходится (причем абсолютно) при всех значения х, т.е. область сходимости х  (–; +).

Заметим, что можно было бы найти область сходимости без использования формул, а применяя непосредственно признак Д" Аламбера:

Так как величина предела не зависит от х и меньше 1, то, значит, ряд сходится при всех значениях х, т.е. при х (-;+).

Пример 20

Найти область сходимости ряда

1!(х +5)+2!(х + 5) 2 +3!(х + 5) 3 +... + п !(х + 5) п +...

Решение .

х + 5), т.е. центр сходимости х 0 = - 5. Числовой коэффициент ряда а п = п !.

Найдем радиус сходимости ряда

.

Таким образом, интервал сходимости состоит из одной точки – центра интервала сходимости х = - 5.

Пример 21

Найти область сходимости ряда
.

Решение.

Данный ряд является степенным рядом по степеням (х –2), т.е.

центр сходимости х 0 = 2. Заметим, что ряд является знакоположительным при любом фиксированном х, так как выражение (х- 2) возводится в степень 2п. Применим к ряду радикальный признак Коши.

Ряд будет сходиться, если величина предела меньше 1, т.е.

,
,
,

значит, радиус сходимости
, тогда интеграл сходимости

,
.

Таким образом, ряд сходится абсолютно при х 
. Обратим внимание, что интеграл сходимости симметричен относительно центра сходимости х о = 2.

Исследуем сходимость ряда на концах интервала сходимости.

Полагая
, получим числовой знакоположительный ряд

Воспользуемся необходимым признаком сходимости:

следовательно, числовой ряд расходится, и точка
является точкой расходимости. Заметим, что при вычислении предела использовали второй замечательный предел.

Полагая
, получим тот же числовой ряд (проверить самостоятельно!), значит, точка
также не входит в интервал сходимости.

Итак, область абсолютной сходимости данного ряда х 
.

2.3. Свойства сходящихся степенных рядов

Мы знаем, что конечная сумма непрерывных функций непрерывна; сумма дифференцируемых функций дифференцируема, причем производная суммы равна сумме производных; конечную сумму можно интегрировать почленно.

Оказывается, для «бесконечных сумм» функций – функциональных рядов в общем случае свойства не имеют места.

Например, рассмотрим функциональный ряд

Очевидно, что все члены ряда – непрерывные функции. Найдем область сходимости этого ряда и его сумму. Для этого найдем частичные суммы ряда

тогда сумма ряда

Таким образом, сумма S (х ) данного ряда, как предел последовательности частичных сумм, существует и конечна при х  (-1;1), значит, этот промежуток является областью сходимости ряда. При этом его сумма является разрывной функцией, так как

Итак, этот пример показывает, что в общем случае свойства конечных сумм не имеют аналога для бесконечных сумм – рядов. Однако для частного случая функциональных рядов – степенных рядов – свойства суммы аналогичны свойствам конечных сумм.

– возможно, сложное окажется не таким уж и сложным;) Да и заголовок этой статьи тоже лукавит – ряды, о которых сегодня пойдёт речь, скорее, не сложные, а «редкоземельные». Однако от них не застрахованы даже студенты-заочники, и поэтому к данному, казалось бы, дополнительному занятию следует отнестись с максимальной серьёзностью. Ведь после его проработки вы сможете расправиться практически с любым «зверем»!

Начнём с классики жанра:

Пример 1

Во-первых, обратим внимание, что это НЕ степенной ряд (напоминаю, что оный имеет вид ) . И, во-вторых, здесь сразу бросается в глаза значение , которое заведомо не может входить в область сходимости ряда. И это уже маленький успех исследования!

Но всё-таки, как прийти к успеху большому? Спешу вас обрадовать – подобные ряды можно решать точно так же, как и степенные – опираясь на признак Даламбера или радикальный признак Коши!

Решение : значение не входит в область сходимости ряда. Это факт существенный, и его нужно обязательно отметить!

Основой же алгоритм работает стандартно. Используя признак Даламбера, найдём интервал сходимости ряда:

Ряд сходится при . Поднимем модуль наверх:

Сразу проконтролируем «нехорошую» точку: значение не вошло в область сходимости ряда.

Исследуем сходимость ряда на «внутренних» концах интервалов:
если , то
если , то

Оба числовых ряда расходятся, так как не выполнен необходимый признак сходимости .

Ответ : область сходимости:

Выполним небольшую аналитическую проверку. Давайте подставим в функциональный ряд какое-нибудь значение из правого интервала, например, :
– сходится по признаку Даламбера .

В случае подстановки значений из левого интервала тоже получаются сходящиеся ряды:
если , то .

И, наконец, если , то ряд – действительно расходится.

Пара простеньких примера для разогрева:

Пример 2

Найти область сходимости функционального ряда

Пример 3

Найти область сходимости функционального ряда

Особенно хорошо разберитесь с «новым» модулем – он сегодня встретится 100500 раз!

Краткие решения и ответы в конце урока.

Использованные алгоритмы вроде бы универсальны и безотказны, но на самом деле это не так – для многих функциональных рядов они часто «пробуксовывают», а то и приводят к ошибочным выводам (и такие примеры я тоже рассмотрю) .

Шероховатости начинаются уже на уровне интерпретации результатов: рассмотрим, например, ряд . Здесь в пределе получаем (проверьте самостоятельно) , и по идее нужно дать ответ, что ряд сходится в единственной точке. Однако, точка «заиграна», а значит, наш «пациент» расходится вообще всюду!

А для ряда «очевидное» решение «по Коши» вообще ничего не даёт:
– для ЛЮБОГО значения «икс».

И возникает вопрос, что же делать? Используем метод, которому как раз будет посвящена основная часть урока! Его можно сформулировать следующим образом:

Прямой анализ числовых рядов при различных значениях

Фактически мы уже начали этим заниматься в Примере 1. Сначала исследуем какое-нибудь конкретное «икс» и соответствующий числовой ряд. Напрашивается взять значение :
– полученный числовой ряд расходится.

И это сразу наталкивает на мысль: а что, если то же самое происходит и в других точках?
Проверим-ка необходимый признак сходимости ряда для произвольного значения :

Точка учтена выше, для всех же остальных «икс» стандартным приёмом организуем второй замечательный предел :

Вывод : ряд расходится на всей числовой прямой

И это решение – самый что ни на есть рабочий вариант!

На практике функциональный ряд часто приходится сопоставлять с обобщённым гармоническим рядом :

Пример 4

Решение : прежде всего, разбираемся с областью определения : в данном случае подкоренное выражение должно быть строго положительным, и, кроме того, должны существовать все члены ряда, начиная с 1-го. Из этого следует то, что:
. При этих значениях получаются условно сходящиеся ряды :
и т.д.

Другие же «икс» не годятся, так, например, при мы получим нелегальный случай , где не существует первых двух членов ряда.

Это всё хорошо, это всё понятно, но остаётся ещё один немаловажный вопрос – как грамотно оформить решение? Я предлагаю схему, которую можно жаргонно назвать «перевод стрелок» на числовые ряды :

Рассмотрим произвольное значение и исследуем сходимость числового ряда . Рутинный признак Лейбница :

1) Данный ряд является знакочередующимся.

2) – члены ряда убывают по модулю. Каждый следующий член ряда по модулю меньше, чем предыдущий: , значит, убывание монотонно.

Вывод: ряд сходится по признаку Лейбница. Как уже отмечалось, сходимость тут условная – по той причине, что ряд – расходится.

Вот так вот – аккуратно и корректно! Ибо за «альфой» мы хитро спрятали все допустимые числовые ряды.

Ответ : функциональный ряд существует и сходится условно при .

Аналогичный пример для самостоятельного решения:

Пример 5

Исследовать сходимость функционального ряда

Примерный образец чистового оформления задания в конце урока.

Вот тебе и «рабочая гипотеза»! – на интервале функциональный ряд сходится!

2) С симметричным интервалом всё прозрачно, рассматриваем произвольные значения и получаем: – абсолютно сходящиеся числовые ряды.

3) И, наконец, «серединка» . Здесь тоже удобно выделить два промежутка.

Рассматриваем произвольное значение из интервала и получаем числовой ряд:

! Опять же – если трудно , подставляйте какое-нибудь конкретное число, например . Впрочем,… вы же хотели трудностей =)

Для всех значений «эн» выполнено , значит:
– таким образом, по признаку сравнения ряд сходится вместе с бесконечно убывающей прогрессией .

Для всех значений «икс» из интервала получаем – абсолютно сходящиеся числовые ряды.

Все «иксы» исследованы, «иксов» больше нет!

Ответ : область сходимости ряда:

Надо сказать, неожиданный результат! И ещё следует добавить, что использование признаков Даламбера или Коши здесь однозначно введёт в заблуждение!

Прямая оценка – это «высший пилотаж» математического анализа, но для этого, конечно, требуется опыт, а где-то даже и интуиция.

А может быть кто-то найдёт путь проще? Пишите! Прецеденты, кстати, есть – несколько раз читатели предлагали более рациональные решения, и я с удовольствием их публиковал.

Успешного вам приземления:)

Пример 11

Найти область сходимости функционального ряда

Моя версия решения совсем близко.

Дополнительный хардкор можно найти в Разделе VI (Ряды) сборника Кузнецова (Задачи 11-13). В Интернете есть готовые решения , но здесь я должен вас предостеречь – многие из них неполные, некорректные, а то и вообще ошибочные. И, к слову, это была одна из причин, по которой появилась на свет данная статья.

Давайте подведём итоги трёх уроков и систематизируем наш инструментарий. Итак:

Чтобы найти интервал(ы) сходимости функционального ряда, можно использовать :

1) Признак Даламбера или признак Коши . И если ряд не степенной – проявляем повышенную осторожность, анализируя полученный результат прямой подстановкой различных значений .

2) Признак равномерной сходимости Вейерштрасса . Не забываем!

3) Сопоставление с типовыми числовыми рядами – рулит в общем случае.

После чего исследуем концы найденных интервалов (если нужно) и получаем область сходимости ряда.

Теперь в вашем распоряжении довольно-таки серьёзный арсенал, который позволит справиться практически с любым тематическим заданием.

Желаю успехов!

Решения и ответы:

Пример 2: Решение : значение не входит в область сходимости ряда.
Используем признак Даламбера:


Ряд сходится при:

Таким образом, интервалы сходимости функционального ряда: .
Исследуем сходимость ряда в конечных точках:
если , то ;
если , то .
Оба числовых ряда расходятся, т.к. не выполнен необходимый признак сходимости.

Ответ : область сходимости: