Решете уравнението на стъпки. Решете уравнението с дроби онлайн. Решаване на реални примери за прости линейни уравнения

В това видео ще анализираме цял набор от линейни уравнения, които се решават с помощта на същия алгоритъм - затова се наричат ​​най-прости.

За начало нека дефинираме: какво е линейно уравнение и кое от тях трябва да се нарече най-простото?

Линейно уравнение е това, в което има само една променлива и то само в първа степен.

Най-простото уравнение означава конструкцията:

Всички останали линейни уравнения се свеждат до най-простите с помощта на алгоритъма:

1. Отворени скоби, ако има такива;
2. Преместете термините, съдържащи променлива, от едната страна на знака за равенство, а термините без променлива към другата;
3. Доведете подобни термини отляво и отдясно на знака за равенство;
4. Разделете полученото уравнение на коефициента на променливата $x$ .

Разбира се, този алгоритъм не винаги помага. Факт е, че понякога след всички тези машинации коефициентът на променливата $x$ се оказва равен на нула. В този случай са възможни два варианта:

1. Уравнението изобщо няма решения. Например, когато получите нещо като $0\cdot x=8$, т.е. отляво е нула, а отдясно е ненулево число. Във видеото по-долу ще разгледаме няколко причини, поради които тази ситуация е възможна.
2. Решението е всички числа. Единственият случай, когато това е възможно, е когато уравнението е сведено до конструкцията $0\cdot x=0$. Съвсем логично е, че колкото и $x$ да заменим, пак ще се окаже „нулата е равна на нула“, т.е. правилно числово равенство.

А сега да видим как работи всичко на примера на реални проблеми.

Примери за решаване на уравнения

Днес се занимаваме с линейни уравнения и то само с най-простите. Най-общо линейно уравнение означава всяко равенство, което съдържа точно една променлива и то стига само до първа степен.

Такива конструкции се решават приблизително по същия начин:

1. На първо място, трябва да отворите скобите, ако има такива (както в последния ни пример);
2. След това донесете подобни
3. И накрая, изолирайте променливата, т.е. всичко, което е свързано с променливата - термините, в които се съдържа - се прехвърля от едната страна, а всичко, което остава без нея, се прехвърля на другата страна.

След това, като правило, трябва да донесете подобно от всяка страна на полученото равенство и след това остава само да разделите на коефициента при "x" и ще получим окончателния отговор.

На теория това изглежда хубаво и просто, но на практика дори опитни гимназисти могат да направят обидни грешки в доста прости линейни уравнения. Обикновено грешки се правят или при отваряне на скоби, или при броене на "плюсове" и "минуси".

Освен това се случва едно линейно уравнение изобщо да няма решения или решението да е цялата числова права, т.е. произволно число. Ще анализираме тези тънкости в днешния урок. Но ние ще започнем, както вече разбрахте, с най-простите задачи.

Схема за решаване на прости линейни уравнения

Като начало, нека още веднъж напиша цялата схема за решаване на най-простите линейни уравнения:

1. Разгънете скобите, ако има такива.
2. Изолирайте променливите, т.е. всичко, което съдържа "x", се прехвърля на едната страна, а без "x" - на другата.
3. Представяме подобни термини.
4. Разделяме всичко на коефициента при "x".

Разбира се, тази схема не винаги работи, тя има определени тънкости и трикове и сега ще ги опознаем.

Решаване на реални примери за прости линейни уравнения

Задача №1

В първата стъпка от нас се изисква да отворим скобите. Но те не са в този пример, така че пропускаме тази стъпка. Във втората стъпка трябва да изолираме променливите. Моля, обърнете внимание: говорим само за отделни термини. Нека напишем:

Даваме подобни термини отляво и отдясно, но това вече е направено тук. Следователно, преминаваме към четвъртата стъпка: разделете на коефициент:

\[\frac(6x)(6)=-\frac(72)(6)\]

Тук получихме отговора.

Задача №2

В тази задача можем да наблюдаваме скобите, така че нека ги разширим:

И отляво, и отдясно виждаме приблизително една и съща конструкция, но нека действаме според алгоритъма, т.е. секвестиращи променливи:

Ето някои като:

В какви корени работи това? Отговор: за всякакви. Следователно можем да запишем, че $x$ е произволно число.

Задача №3

Третото линейно уравнение вече е по-интересно:

\[\left(6-x \right)+\left(12+x \right)-\left(3-2x \right)=15\]

Тук има няколко скоби, но те не се умножават по нищо, а просто имат различни знаци пред тях. Нека ги разбием:

Извършваме втората стъпка, която вече ни е известна:

\[-x+x+2x=15-6-12+3\]

Да изчислим:

Изпълняваме последната стъпка - разделяме всичко на коефициента при "x":

\[\frac(2x)(x)=\frac(0)(2)\]

Неща, които трябва да запомните, когато решавате линейни уравнения

Ако пренебрегнем твърде простите задачи, бих искал да кажа следното:

• Както казах по-горе, не всяко линейно уравнение има решение - понякога просто няма корени;
• Дори и да има корени, нула може да влезе сред тях - няма нищо лошо в това.

Нулата е същото число като останалите, не трябва по някакъв начин да го разграничавате или да предполагате, че ако получите нула, значи сте направили нещо нередно.

Друга особеност е свързана с разширяването на скоби. Моля, обърнете внимание: когато има „минус“ пред тях, ние го премахваме, но в скоби променяме знаците на противоположно. И тогава можем да го отворим според стандартните алгоритми: ще получим това, което видяхме в изчисленията по-горе.

Разбирането на този прост факт ще ви помогне да избегнете глупави и болезнени грешки в гимназията, когато подобни действия се приемат за даденост.

Решаване на сложни линейни уравнения

Нека да преминем към по-сложни уравнения. Сега конструкциите ще станат по-сложни и ще се появи квадратична функция при извършване на различни трансформации. Въпреки това, не бива да се страхувате от това, защото ако според намерението на автора решим линейно уравнение, тогава в процеса на трансформация всички мономи, съдържащи квадратична функция, непременно ще бъдат намалени.

Пример №1

Очевидно първата стъпка е да отворите скобите. Нека направим това много внимателно:

Сега нека вземем поверителност:

\[-x+6((x)^(2))-6((x)^(2))+x=-12\]

Ето някои като:

Очевидно това уравнение няма решения, така че в отговора пишем, както следва:

\[\ разнообразие \]

или без корени.

Пример №2

Извършваме същите стъпки. Първа стъпка:

Нека преместим всичко с променлива наляво, а без нея - надясно:

Ето някои като:

Очевидно това линейно уравнение няма решение, затова го пишем така:

\[\varnothing\],

или без корени.

Нюанси на решението

И двете уравнения са напълно решени. На примера на тези два израза отново се уверихме, че дори и в най-простите линейни уравнения всичко може да не е толкова просто: може да има или едно, или нито едно, или безкрайно много. В нашия случай разгледахме две уравнения, и в двете просто няма корени.

Но бих искал да насоча вниманието ви към друг факт: как да работите със скоби и как да ги отворите, ако пред тях има знак минус. Помислете за този израз:

Преди да отворите, трябва да умножите всичко по "x". Моля, обърнете внимание: умножете всеки отделен термин. Вътре има два члена - съответно два члена и се умножава.

И едва след като тези на пръв поглед елементарни, но много важни и опасни трансформации бъдат завършени, скобата може да се отвори от гледна точка, че след нея има знак минус. Да, да: само сега, когато трансформациите са направени, си спомняме, че има знак минус пред скобите, което означава, че всичко надолу просто сменя знаците. В същото време самите скоби изчезват и най-важното е, че предният „минус“ също изчезва.

Правим същото с второто уравнение:

Неслучайно обръщам внимание на тези дребни, на пръв поглед незначителни факти. Защото решаването на уравнения винаги е последователност от елементарни трансформации, където невъзможността за ясно и компетентно извършване на прости действия води до факта, че гимназистите идват при мен и се научават да решават отново такива прости уравнения.

Разбира се, ще дойде ден, когато ще усъвършенствате тези умения до автоматизма. Вече не е нужно да извършвате толкова много трансформации всеки път, ще напишете всичко на един ред. Но докато само учите, трябва да напишете всяко действие поотделно.

Решаване на още по-сложни линейни уравнения

Това, което ще решим сега, трудно може да се нарече най-простата задача, но смисълът остава същият.

Задача №1

\[\left(7x+1 \right)\left(3x-1 \right)-21((x)^(2))=3\]

Нека умножим всички елементи в първата част:

Да направим отстъпление:

Ето някои като:

Нека направим последната стъпка:

\[\frac(-4x)(4)=\frac(4)(-4)\]

Ето нашия окончателен отговор. И въпреки факта, че в процеса на решаване имахме коефициенти с квадратична функция, те обаче взаимно се анихилираха, което прави уравнението точно линейно, а не квадратно.

Задача №2

\[\left(1-4x \right)\left(1-3x \right)=6x\left(2x-1 \right)\]

Нека направим първата стъпка внимателно: умножете всеки елемент от първата скоба по всеки елемент във втората. След трансформациите трябва да се получат общо четири нови термина:

И сега внимателно извършете умножението във всеки член:

Нека преместим термините с "x" наляво, а без - надясно:

\[-3x-4x+12((x)^(2))-12((x)^(2))+6x=-1\]

Ето подобни термини:

Получихме категоричен отговор.

Нюанси на решението

Най-важната забележка за тези две уравнения е следната: щом започнем да умножаваме скоби, в които има повече от член, тогава това се прави според следното правило: вземаме първия член от първия и умножаваме с всеки елемент от втория; след това вземаме втория елемент от първия и по същия начин умножаваме с всеки елемент от втория. В резултат получаваме четири термина.

Върху алгебричния сбор

С последния пример бих искал да напомня на учениците какво е алгебрична сума. В класическата математика под $1-7$ имаме предвид проста конструкция: изваждаме седем от едно. В алгебрата имаме предвид следното: към числото "едно" добавяме друго число, а именно "минус седем". Тази алгебрична сума се различава от обичайната аритметична сума.

Веднага след като извършвате всички трансформации, всяко събиране и умножение, започнете да виждате конструкции, подобни на описаните по-горе, просто няма да имате никакви проблеми в алгебрата, когато работите с полиноми и уравнения.

В заключение, нека разгледаме още няколко примера, които ще бъдат дори по-сложни от тези, които току-що разгледахме, и за да ги разрешим, ще трябва леко да разширим нашия стандартен алгоритъм.

Решаване на уравнения с дроб

За да решим такива задачи, ще трябва да добавим още една стъпка към нашия алгоритъм. Но първо ще напомня нашия алгоритъм:

1. Отворени скоби.
2. Отделни променливи.
3. Донесете подобни.
4. Разделете по коефициент.

Уви, този прекрасен алгоритъм, при цялата си ефективност, не е съвсем подходящ, когато имаме дроби пред нас. И в това, което ще видим по-долу, имаме дроб отляво и отдясно и в двете уравнения.

Как да се работи в този случай? Да, много е просто! За да направите това, трябва да добавите още една стъпка към алгоритъма, която може да се извърши както преди първото действие, така и след него, а именно да се отървете от дроби. По този начин алгоритъмът ще бъде както следва:

1. Отървете се от дроби.
2. Отворени скоби.
3. Отделни променливи.
4. Донесете подобни.
5. Разделете по коефициент.

Какво означава "да се отървеш от дроби"? И защо е възможно да се направи това както след, така и преди първата стандартна стъпка? Всъщност в нашия случай всички дроби са числови по отношение на знаменателя, т.е. навсякъде знаменателят е просто число. Следователно, ако умножим и двете части на уравнението по това число, тогава ще се отървем от дробите.

Пример №1

\[\frac(\left(2x+1 \right)\left(2x-3 \right))(4)=((x)^(2))-1\]

Нека се отървем от дробите в това уравнение:

\[\frac(\left(2x+1 \right)\left(2x-3 \right)\cdot 4)(4)=\left(((x)^(2))-1 \right)\cdot 4\]

Моля, обърнете внимание: всичко се умножава по „четири“ веднъж, т.е. само защото имате две скоби, не означава, че трябва да умножите всяка от тях по "четири". Нека напишем:

\[\left(2x+1 \right)\left(2x-3 \right)=\left(((x)^(2))-1 \right)\cdot 4\]

Сега нека го отворим:

Извършваме изолиране на променлива:

Извършваме редукция на подобни термини:

\[-4x=-1\вляво| :\ляво(-4 \вдясно) \вдясно.\]

\[\frac(-4x)(-4)=\frac(-1)(-4)\]

Получихме окончателното решение, преминаваме към второто уравнение.

Пример №2

\[\frac(\left(1-x \right)\left(1+5x \right))(5)+((x)^(2))=1\]

Тук извършваме всички същите действия:

\[\frac(\left(1-x \right)\left(1+5x \right)\cdot 5)(5)+((x)^(2))\cdot 5=5\]

\[\frac(4x)(4)=\frac(4)(4)\]

Проблема решен.

Всъщност това е всичко, което исках да кажа днес.

Ключови точки

Основните констатации са както следва:

• Познайте алгоритъма за решаване на линейни уравнения.
• Възможност за отваряне на скоби.
• Не се притеснявайте, ако някъде имате квадратични функции, най-вероятно в процеса на по-нататъшни трансформации те ще бъдат намалени.
• Корените в линейните уравнения, дори най-простите, са три вида: един единствен корен, цялата числова права е корен, корени изобщо няма.

Надявам се този урок да ви помогне да овладеете една проста, но много важна тема за по-нататъшното разбиране на цялата математика. Ако нещо не е ясно, отидете на сайта, решете примерите, представени там. Очаквайте ви още много интересни неща!

Онлайн калкулаторът на дроби ви позволява да извършвате прости аритметични операции с дроби: събиране на дроби, изваждане на дроби, умножение на дроби, деление на дроби. За да направите изчисления, попълнете полетата, съответстващи на числителите и знаменателите на две дроби.

Дроби по математикасе нарича число, представляващо част от единица или няколко нейни части.

Обикновената дроб се записва като две числа, обикновено разделени с хоризонтална линия, указваща знака за деление. Числото над лентата се нарича числител. Числото под чертата се нарича знаменател. Знаменателят на дроб показва броя на равните части, на които е разделено цялото, а числителят на дроба показва броя на тези части от взетото цяло.

Дробите са правилни и грешни.

• Правилна дроб е тази, чийто числител е по-малък от знаменателя.
• Неправилна дроб е, когато числителят е по-голям от знаменателя.

Смесена дроб е дроб, записана като цяло число и правилна дроб и се разбира като сбор от това число и дробната част. Съответно, дроб, която няма цяла част, се нарича проста дроб. Всяка смесена дроб може да бъде превърната в неправилна проста дроб.

За да преобразувате смесена дроб в обикновена, е необходимо да добавите произведението на цялата част и знаменателя към числителя на дроба:

Как да преобразуваме обикновена дроб в смесена

За да преобразувате обикновена дроб в смесена, трябва:

1. Разделете числителя на дроб на знаменателя
2. Резултатът от разделянето ще бъде цялата част
3. Остатъкът от клона ще бъде числителят

Как да преобразуваме обикновена дроб в десетична

За да преобразувате дроб в десетична дроб, трябва да разделите числителя на знаменателя.

За да преобразувате десетична дроб в обикновена дроб, трябва:

Как да конвертирате дроб в процент

За да преобразувате обикновена или смесена дроб в процент, трябва да я преобразувате в десетична дроб и да умножите по 100.

Как да конвертирате проценти във дроби

За да преобразувате процентите във дроби, е необходимо да получите десетична дроб от проценти (делите на 100), след което да преобразувате получената десетична дроб в обикновена.

Събиране на дроби

Алгоритъмът за добавяне на две дроби е както следва:

1. Съберете дроби, като добавите техните числители.

Изваждане на дроби

Алгоритъм на действия при изваждане на две дроби:

1. Преобразувайте смесените дроби в обикновени (отървете се от цялата част).
2. Доведете дробите до общ знаменател. За да направите това, трябва да умножите числителя и знаменателя на първата дроб по знаменателя на втората дроб и да умножите числителя и знаменателя на втората дроб по знаменателя на първата дроб.
3. Извадете една дроб от друга, като извадите числителя на втората дроб от числителя на първата.
4. Намерете най-големия общ делител (НДО) на числителя и знаменателя и намалете дроба, като разделите числителя и знаменателя на НОД.
5. Ако числителят на крайната дроб е по-голям от знаменателя, тогава изберете цялата част.

Умножение на дроби

Алгоритъм на действия при умножаване на две дроби:

1. Преобразувайте смесените дроби в обикновени (отървете се от цялата част).
2. Намерете най-големия общ делител (НДО) на числителя и знаменателя и намалете дроба, като разделите числителя и знаменателя на НОД.
3. Ако числителят на крайната дроб е по-голям от знаменателя, тогава изберете цялата част.

Деление на дроби

Алгоритъм на действия при разделяне на две дроби:

1. Преобразувайте смесените дроби в обикновени (отървете се от цялата част).
2. За да разделите дроби, трябва да преобразувате втората дроб, като размените нейния числител и знаменател и след това умножите дробите.
3. Умножете числителя на първата дроб по числителя на втората дроб и знаменателя на първата дроб по знаменателя на втората.
4. Намерете най-големия общ делител (НДО) на числителя и знаменателя и намалете дроба, като разделите числителя и знаменателя на НОД.
5. Ако числителят на крайната дроб е по-голям от знаменателя, тогава изберете цялата част.

Онлайн калкулатори и конвертори:

Уравнение с едно неизвестно, което след отваряне на скобите и намаляване на подобни членове приема формата

ах + b = 0, където a и b са произволни числа, се нарича линейно уравнение с едно неизвестно. Днес ще разберем как да решим тези линейни уравнения.

Например всички уравнения:

2x + 3 \u003d 7 - 0,5x; 0,3х = 0; x / 2 + 3 \u003d 1/2 (x - 2) - линеен.

Стойността на неизвестното, която превръща уравнението в истинско равенство, се нарича решение или коренът на уравнението .

Например, ако в уравнението 3x + 7 \u003d 13 заместим числото 2 вместо неизвестното x, тогава получаваме правилното равенство 3 2 + 7 \u003d 13. Това означава, че стойността x = 2 е решението или корена на уравнението.

И стойността x \u003d 3 не превръща уравнението 3x + 7 \u003d 13 в истинско равенство, тъй като 3 2 + 7 ≠ 13. Следователно стойността x = 3 не е решение или корен на уравнението.

Решението на всякакви линейни уравнения се свежда до решението на уравнения от вида

ах + b = 0.

Прехвърляме свободния член от лявата страна на уравнението надясно, като променяме знака пред b на обратния, получаваме

Ако a ≠ 0, тогава x = – b/a .

Пример 1 Решете уравнението 3x + 2 =11.

Прехвърляме 2 от лявата страна на уравнението надясно, докато сменяме знака пред 2 на обратния, получаваме
3x \u003d 11 - 2.

Тогава нека направим изваждането
3x = 9.

За да намерите x, трябва да разделите продукта на известен фактор, т.е.
х = 9:3.

Така че стойността x = 3 е решението или корена на уравнението.

Отговор: х = 3.

Ако a = 0 и b = 0, тогава получаваме уравнението 0x \u003d 0. Това уравнение има безкрайно много решения, тъй като при умножаване на произволно число по 0 получаваме 0, но b също е 0. Решението на това уравнение е произволно число.

Пример 2Решете уравнението 5(x - 3) + 2 = 3 (x - 4) + 2x - 1.

Нека разширим скобите:
5x - 15 + 2 \u003d 3x - 12 + 2x - 1.

5x - 3x - 2x \u003d - 12 - 1 + 15 - 2.

Ето подобни членове:
0x = 0.

Отговор: x е произволно число.

Ако a = 0 и b ≠ 0, тогава получаваме уравнението 0x = - b. Това уравнение няма решения, тъй като при умножаване на произволно число по 0 получаваме 0, но b ≠ 0.

Пример 3Решете уравнението x + 8 = x + 5.

Нека групираме термините, съдържащи неизвестни от лявата страна, и свободните термини от дясната страна:
x - x \u003d 5 - 8.

Ето подобни членове:
0x = - 3.

Отговор: няма решения.

На Фигура 1 е показана схемата за решаване на линейното уравнение

Нека съставим обща схема за решаване на уравнения с една променлива. Помислете за решението на пример 4.

Пример 4 Нека решим уравнението

1) Умножете всички членове на уравнението по най-малкото общо кратно на знаменателите, равно на 12.

2) След намаляване получаваме
4 (x - 4) + 3 2 (x + 1) - 12 = 6 5 (x - 3) + 24x - 2 (11x + 43)

3) За да разделите членове, съдържащи неизвестни и свободни членове, отворете скобите:
4x - 16 + 6x + 6 - 12 \u003d 30x - 90 + 24x - 22x - 86.

4) В едната част групираме термините, съдържащи неизвестни, а в другата - свободни термини:
4x + 6x - 30x - 24x + 22x \u003d - 90 - 86 + 16 - 6 + 12.

5) Ето подобни членове:
- 22x = - 154.

6) Разделете на - 22 , Получаваме
х = 7.

Както можете да видите, коренът на уравнението е седем.

Общо взето такива уравненията могат да бъдат решени по следния начин:

а) приведете уравнението до целочислен вид;

б) отворени скоби;

в) групирайте членовете, съдържащи неизвестното в едната част на уравнението, и свободните членове в другата;

г) довеждат подобни членове;

д) решава уравнение от вида aх = b, което се получава след привеждане на подобни членове.

Тази схема обаче не е необходима за всяко уравнение. При решаване на много по-прости уравнения трябва да се започне не от първото, а от второто ( Пример. 2), трети ( Пример. тринадесет) и дори от петия етап, както в пример 5.

Пример 5Решете уравнението 2x = 1/4.

Намираме неизвестното x \u003d 1/4: 2,
х = 1/8 .

Помислете за решението на някои линейни уравнения, срещани на главния държавен изпит.

Пример 6Решете уравнение 2 (x + 3) = 5 - 6x.

2x + 6 = 5 - 6x

2x + 6x = 5 - 6

Отговор: - 0,125

Пример 7Решете уравнението - 6 (5 - 3x) \u003d 8x - 7.

– 30 + 18x = 8x – 7

18x - 8x = - 7 +30

Отговор: 2.3

Пример 8 Решете уравнението

3(3x - 4) = 4 7x + 24

9x - 12 = 28x + 24

9x - 28x = 24 + 12

Пример 9Намерете f(6), ако f (x + 2) = 3 7

Решение

Тъй като трябва да намерим f(6) и знаем f (x + 2),
тогава х + 2 = 6.

Решаваме линейното уравнение x + 2 = 6,
получаваме x = 6 - 2, x \u003d 4.

Ако х = 4 тогава
f(6) = 3 7-4 = 3 3 = 27

Отговор: 27.

Ако все още имате въпроси, има желание да се занимавате с решението на уравнения по-задълбочено, запишете се за моите уроци в ГРАФИКА. Ще се радвам да ви помогна!

TutorOnline също препоръчва да гледате нов видео урок от нашия преподавател Олга Александровна, който ще ви помогне да разберете както линейните уравнения, така и други.

сайт, с пълно или частично копиране на материала е необходима връзка към източника.

Какво представляват ирационалните уравнения и как да ги решаваме

Уравнения, в които променливата се съдържа под знака на радикала или под знака на повишаване на дробна степен, се наричат ирационално. Когато работим с дробна степен, ние се лишаваме от много математически операции за решаване на уравнението, така че ирационалните уравнения се решават по специален начин.

Ирационалните уравнения обикновено се решават чрез повишаване на двете страни на уравнението на една и съща степен. В същото време, повишаването на двете части на уравнението до една и съща нечетна степен е еквивалентна трансформация на уравнението, а на четна не е еквивалентна. Такава разлика се получава поради такива характеристики на степенуване, като например, ако се повдигне на четна степен, тогава отрицателните стойности се „загубват“.

Смисълът на издигането на двете страни на ирационалното уравнение до степен е да се отървем от "ирационалността". Следователно, ние трябва да повдигнем двете части на ирационалното уравнение до такава степен, че всички дробни степени на двете части на уравнението да се превърнат в цели числа. След това можете да потърсите решение на това уравнение, което ще съвпада с решенията на ирационалното уравнение, с тази разлика, че в случай на повишаване на четна степен знакът се губи и крайните решения ще изискват проверка и не всички ще работят.

По този начин основната трудност е свързана с издигането на двете части на уравнението до една и съща четна степен - поради нееквивалентността на трансформацията могат да се появят външни корени. Затова е задължително да се проверят всички намерени корени. Проверката на намерените корени най-често се забравя от тези, които решават ирационално уравнение. Също така не винаги е ясно до каква степен е необходимо да се повдигне ирационално уравнение, за да се отървем от ирационалността и да се реши. Нашият интелигентен калкулатор просто е проектиран да решава ирационално уравнение и автоматично да проверява всички корени, което ще премахне забравата.

Безплатен онлайн калкулатор на ирационални уравнения

Нашият безплатен решател ще ви позволи да решите онлайн ирационално уравнение с всякаква сложност за броени секунди. Всичко, което трябва да направите, е просто да въведете данните си в калкулатора. Можете също да научите как да решите уравнението на нашия уебсайт. И ако имате някакви въпроси, можете да ги зададете в нашата група VKontakte.

Възлагане на услугата. Матричният калкулатор е предназначен за решаване на системи от линейни уравнения по матричен начин (вижте пример за решаване на подобни задачи).

Инструкция. За онлайн решение трябва да изберете вида на уравнението и да зададете размерността на съответните матрици. където A, B, C са дадени матрици, X е желаната матрица. Матричните уравнения от вида (1), (2) и (3) се решават чрез обратната матрица A -1 . Ако е даден изразът A X - B = C, тогава е необходимо първо да се съберат матриците C + B и да се намери решение за израза A X = D , където D = C + B . Ако е даден изразът A*X = B 2, тогава матрицата B трябва първо да бъде квадратирана.

Също така се препоръчва да се запознаете с основните операции с матрици.

Пример №1. Упражнение. Намерете решение на матрично уравнение
Решение. Означете:
Тогава матричното уравнение ще бъде записано във вида: A·X·B = C.
Детерминантата на матрица A е detA=-1
Тъй като A е неособена матрица, има обратна матрица A -1 . Умножете двете страни на уравнението отляво по A -1: Умножете двете страни на това уравнение отляво по A -1 и отдясно по B -1: A -1 A X B B -1 = A -1 C B -1 . Тъй като A A -1 = B B -1 = E и E X = X E = X, тогава X = A -1 C B -1

Обратна матрица A -1:
Намерете обратната матрица B -1 .
Транспонирана матрица B T:
Обратна матрица B -1:
Търсим матрицата X по формулата: X = A -1 C B -1

Отговор:

Пример №2. Упражнение.Решаване на матрично уравнение
Решение. Означете:
Тогава матричното уравнение ще бъде записано във вида: A X = B.
Детерминантата на матрица A е detA=0
Тъй като A е изродена матрица (детерминантата е 0), следователно, уравнението няма решение.

Пример №3. Упражнение. Намерете решение на матрично уравнение
Решение. Означете:
Тогава матричното уравнение ще бъде записано във вида: X·A = B.
Детерминантата на матрица А е detA=-60
Тъй като A е неособена матрица, има обратна матрица A -1 . Умножете отдясно двете страни на уравнението по A -1: X A A -1 = B A -1 , от което намираме, че X = B A -1
Намерете обратната матрица A -1 .
Транспонирана матрица A T: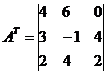
Обратна матрица A -1:
Търсим матрицата X по формулата: X = B A -1


Отговор: >