4. Случайные величины и их распределения

Гамма-распределения

Перейдем к семейству гамма-распределений. Они широко применяются в экономике и менеджменте, теории и практике надежности и испытаний, в различных областях техники, метеорологии и т.д. В частности, гамма-распределению подчинены во многих ситуациях такие величины, как общий срок службы изделия, длина цепочки токопроводящих пылинок, время достижения изделием предельного состояния при коррозии, время наработки до k -го отказа, k = 1, 2, …, и т.д. Продолжительность жизни больных хроническими заболеваниями, время достижения определенного эффекта при лечении в ряде случаев имеют гамма-распределение. Это распределение наиболее адекватно для описания спроса в экономико-математических моделях управления запасами (логистики).

Плотность гамма-распределения имеет вид

Плотность вероятности в формуле (17) определяется тремя параметрами a , b , c , где a >0, b >0. При этом a является параметром формы, b - параметром масштаба и с - параметром сдвига. Множитель 1/Γ(а) является нормировочным, он введен, чтобы

Здесь Γ(а) - одна из используемых в математике специальных функций, так называемая "гамма-функция", по которой названо и распределение, задаваемое формулой (17),

При фиксированном а формула (17) задает масштабно-сдвиговое семейство распределений, порождаемое распределением с плотностью

(18)

Распределение вида (18) называется стандартным гамма-распределением. Оно получается из формулы (17) при b = 1 и с = 0.

Частным случаем гамма-распределений при а = 1 являются экспоненциальные распределения (с λ = 1/ b ). При натуральном а и с =0 гамма-распределения называются распределениями Эрланга. С работ датского ученого К.А.Эрланга (1878-1929), сотрудника Копенгагенской телефонной компании, изучавшего в 1908-1922 гг. функционирование телефонных сетей, началось развитие теории массового обслуживания. Эта теория занимается вероятностно-статистическим моделированием систем, в которых происходит обслуживание потока заявок, с целью принятия оптимальных решений. Распределения Эрланга используют в тех же прикладных областях, в которых применяют экспоненциальные распределения. Это основано на следующем математическом факте: сумма k независимых случайных величин, экспоненциально распределенных с одинаковыми параметрами λ и с , имеет гамма-распределение с параметром формы а = k , параметром масштаба b = 1/λ и параметром сдвига kc . При с = 0 получаем распределение Эрланга.

Если случайная величина X имеет гамма-распределение с параметром формы а таким, что d = 2 a - целое число, b = 1 и с = 0, то 2Х имеет распределение хи-квадрат с d степенями свободы.

Случайная величина X с гвмма-распределением имеет следующие характеристики:

Математическое ожидание М(Х) = ab + c ,

Дисперсию D (X ) = σ 2 = ab 2 ,

Гамма-распределение

Гамма-распределение является двухпараметрическим распределением. Оно занимает достаточно важное место в теории и практике надежности. Плотность распределения имеет ограничение с одной стороны (). Если параметр а формы кривой распределения принимает целое значение, это свидетельствует о вероятности появления такого же числа событий (например, отказов)

при условии, что они независимы и появляются с постоянной интенсивностью λ (см. рис. 4.4).

Гамма-распределение широко применяют при описании появления отказов стареющих элементов, времени восстановления, наработки на отказ резервированных систем. При различных параметрах гамма-распределение принимает разнообразные формы, что и объясняет его широкое применение.

Плотность вероятности гамма-распределения определяется равенством

где λ > 0, α > 0.

Кривые плотности распределения приведены на рис. 4.5.

Рис. 4.5.

Функция распределения

Математическое ожидание и дисперсия равны соответственно

При α < 1 интенсивность отказов монотонно убывает, что соответствует периоду приработки изделия, при α > 1 – возрастает, что характерно для периода изнашивания и старения элементов.

При α = 1 гамма-распределение совпадает с экспоненциальным распределением, при α > 10 гамма-распределение приближается к нормальному закону. Если а принимает значения произвольных целых положительных чисел, то такое гамма-распределение называют распределением Эрланга. Если λ = 1/2, а значение а кратно 1 /2, то гамма-распределение совпадает с распределением χ2 (хи-квадрат ).

Установление функции распределения показателей надежности по результатам обработки данных статистической информации

Наиболее полной характеристикой надежности сложной системы является закон распределения, выраженный в виде функции распределения, плотности распределения или функции надежности.

О виде теоретической функции распределения можно судить по эмпирической функции распределения (рис. 4.6), которая определяется из соотношения

где т, – число отказов на интервале времени t; N – объем испытаний; t i < t < t i+1 – интервал времени, на котором определяют эмпирическую функцию.

Рис. 4.6.

Построение эмпирической функции осуществляют, выполняя суммирование приращений, полученных на каждом интервале времени:

где k – число интервалов.

Эмпирическая функция надежности является функцией, противоположной функции распределения; ее определяют по формуле

Оценку плотности вероятности находят по гистограмме. Построение гистограммы сводится к следующему. Всю область значений времени t разбивают на интервалы t 1, t 2, ..., t i и для каждого из них осуществляют оценку плотности вероятности по формуле

где т i – число отказов на i -м интервале, i = 1, 2,..., k; (t i+1 – t i) – отрезок времени i -го интервала; N – объем испытаний; k – число интервалов.

Пример гистограммы приведен на рис. 4.7.

Рис. 4.7.

Сглаживая ступенчатую гистограмму плавной кривой, но ее виду можно судить о законе распределения случайной величины. В практике для сглаживания кривой часто, например, используют метод наименьших квадратов. Для более точного установления закона распределения необходимо, чтобы число интервалов было не менее пяти, а число реализаций, попадающих в каждый интервал, – не менее десяти.

Разночтения в понимании терминологии надежности

Проблема терминологии является достаточно сложной в различных областях науки и человеческой деятельности в целом. Известно, что споры о терминах ведутся в течение многих веков. Если коснуться переводов стихотворений, то можно увидеть яркое подтверждение этой мысли. Например, переводы такого всемирно известного шедевра, как "Гамлет", у Б. Л. Пастернака и Π. П. Гнедича резко отличаются. У первого из них смысл трагедии перевешивает музыку стиха, в отличие от второго. А оригинал "Гамлета", написанный языком XVI в., труден для понимания неангличанам, да и англичанам тоже, поскольку сам язык сильно эволюционировал за несколько веков, как, собственно, и любой другой язык в соответствии с законом синхронизма-десинхронизма.

Аналогичная картина наблюдается и в мировых религиях. Перевод Библии с церковно-славянского на русский язык, длившийся 25 лет, "развел" (вплоть до остановки перевода) святителя Филарета Московского (Дроздова) и крупнейшего церковного писателя – святителя Феофана Затворника (в ближайшее время запланировано издание собрания его сочинений в 42 т.). Переводы и уточнения "книги книг" Библии "переводят" людей в лагеря непримиримых врагов по жизни в нашем мире. Рождаются секты, еретики и герои, иногда даже льется кровь. А многочисленные переводы на русский язык основополагающей в сфере философии работы Иммануила Канта "Критика чистого разума" только укрепляют справедливость нашего тезиса о сложности проблемы терминологии (сверхбольшая система) в различных областях науки и человеческой деятельности в целом.

Антиномические явления имеют место в области науки и техники. Одно из решений проблемы обеспечения корректности и адекватности терминологии изложил Г. Лейбниц. Он в плане развития науки и техники в XVII в. предлагал для прекращения споров давать определения терминов с помощью универсального языка в цифровой форме (0011...).

Отметим, что в науке о надежности путь определения терминов традиционно решается на государственном уровне с помощью государственных стандартов (ГОСТов). Однако появление все более высокоинтеллектуальных технических систем, взаимодействие и сближение живых и неживых объектов, в них функционирующих, ставит новые, весьма трудные задачи обучения в педагогике и психологии, заставляет искать творческие компромиссные решения.

У зрелого и поработавшего в конкретной научной области, и в частности в области надежности, сотрудника актуальность вопросов терминологии не вызывает сомнений. Как писал Готфрид Вильгельм Лейбниц (в работе о создании универсального языка), споров было бы меньше, если бы термины были определены.

Разночтения в понимании терминологии надежности попытаемся сгладить следующими замечаниями.

Мы говорим "функция распределения" (ФР), опуская слово "наработка" или "отказ". Наработка чаще всего понимается как категория времени. Для невосстанавливаемых систем по смыслу более правильно надо говорить – интегральная ФР наработки до отказа, а для восстанавливаемых – наработка па отказ. А поскольку наработку чаще всего понимают как случайную величину, применяется отождествление вероятности безотказной работы (ВБР) и (1 – ФР), называемой в этом случае функцией надежности (ФН). Целостность такового подхода достигается за счет полной группы событий . Тогда

ВБР = ФН = 1 – ФР.

То же справедливо в отношении плотности распределения (ПР), которая является первой производной от ФР, в частности по времени, и, образно говоря, характеризует "скорость" появления отказов.

Полнота описания надежности изделия (в частности, для изделий разового применения), включающая динамику устойчивости поведения, характеризуется интенсивностью отказов через отношение ПР к ВБР и физически понимается как смена состояния изделия, а математически – введена в теории массового обслуживания через понятие потока отказов и ряд допущений в отношении самих отказов (стационарность, ординарность и др.).

Интересующихся этими вопросами, возникающими при выборе показателей надежности на этапе проектирования изделий, можно отослать к трудам таких именитых авторов, как А. М. Половко, Б. В. Гнеденко, Б. Р. Левин – выходцев из лаборатории надежности при Московском университете, руководимой А. Н. Колмогоровым, а также А. Я. Хинчина, E. С. Венцель, И. А. Ушакова, Г. В. Дружинина, А. Д. Соловьева, Ф. Байхельта, Ф. Прошана – основателей статистической теории надежности.

• См.: Колмогоров А. Н. Основные понятия теории вероятностей. М. : Мир, 1974.

Равномерное распределение. Непрерывная величина Х распределена равномерно на интервале (a , b ), если все ее возможные значения находятся на этом интервале и плотность распределения вероятностей постоянна:

Для случайной величины Х , равномерно распределенной в интервале (a , b ) (рис. 4), вероятность попадания в любой интервал (x 1 , x 2 ), лежащий внутри интервала (a , b ), равна:

(30)


Рис. 4. График плотности равномерного распределения

Примерами равномерно распределенных величин являются ошибки округления. Так, если все табличные значения некоторой функции округлены до одного и того же разряда , то выбирая наугад табличное значение, мы считаем, что ошибка округления выбранного числа есть случайная величина, равномерно распределенная в интервале

Показательное распределение. Непрерывная случайная величина Х имеет показательное распределение

(31)

График плотности распределения вероятностей (31) представлен на рис. 5.

Рис. 5. График плотности показательного распределения

Время Т безотказной работы компьютерной системы есть случайная величина, имеющая показательное распределение с параметром λ , физический смысл которого – среднее число отказов в единицу времени, не считая простоев системы для ремонта.

Нормальное (гауссово) распределение. Случайная величина Х имеет нормальное (гауссово) распределение , если плотность распределения ее вероятностей определяется зависимостью:

(32)

где m = M (X ) , .

При нормальное распределение называется стандартным .

График плотности нормального распределения (32) представлен на рис. 6.

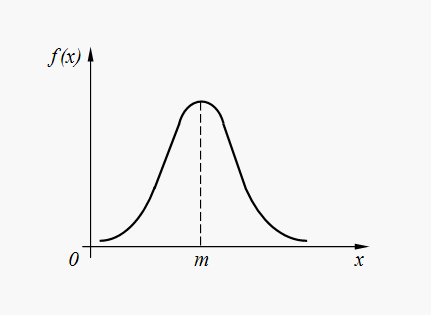
Рис. 6. График плотности нормального распределения

Нормальное распределение является наиболее часто встречающимся в различных случайных явлениях природы. Так, ошибки выполнения команд автоматизированным устройством, ошибки вывода космического корабля в заданную точку пространства, ошибки параметров компьютерных систем и т.д. в большинстве случаев имеют нормальное или близкое к нормальному распределение. Более того, случайные величины, образованные суммированием большого количества случайных слагаемых, распределены практически по нормальному закону.

Гамма-распределение. Случайная величина Х имеет гамма-распределение , если плотность распределения ее вероятностей выражается формулой:

(33)

где – гамма-функция Эйлера.

THE PRACTICE OF APPLYING GAMMA DISTRIBUTION THE THEORY OF RELIABILITY OF TECHNICAL SYSTEMS

Ruslan Litvinenko

candidate of technical sciences, docent, associate professor at the sub-department of electrotechnical complexes and systems, Kazan state power engineering university,

Russia, Republic of Tatarstan, Kazan

Aleksandr Jamshhikov

master student ,

Russia, Republic of Tatarstan, Kazan

Aleksej Bagaev

master student Kazan state power engineering university ,

Russia, Republic of Tatarstan, Kazan

АННОТАЦИЯ

В практике эксплуатации технических систем в большинстве случаев приходится иметь дело с вероятностными (случайными) процессами, когда функция отражает аргумент с некоторой вероятностью. В условиях неопределенности информации о законе распределения времени наступления отказов вследствие малых объемов статистических данных, что как правило бывает на начальных этапах разработки техники, исследователю приходится принимать решение о выборе априорной модели надежности, исходя из опыта предыдущей эксплуатации прототипов или аналогов. Систематизация информации о практическом использовании основных распределений при прогнозировании и оценке надежности различных технических систем является актуальной научной задачей.

В основе изложенного материала лежит систематизация информации опубликованной литературе, и представляющая анализ результатов модельных и экспериментальных исследований надежности техники, а также статистические данные полученные в ходе эксплуатации.

Представленная теоретическая информация о применении гамма-распределения в теории надежности может быть использована в качестве первого приближения, и подлежит обязательному уточнению, с использованием различных критериев проверки гипотез, по мере увеличения объема статистических данных в ходе последующих испытаний.

Надо иметь достаточно оснований для применения экспоненциального закона распределения, как и любого другого. Поэтому статья может быть полезна исследователям на ранних этапах разработки или модернизации технической системы, в качестве априорной информации для построения моделей и критериев, используемых для обеспечения и контроля надежности.

ABSTRACT

In practice, operation of technical systems in most cases have to deal with stochastic (random) processes, when the function reflects the argument with a certain probability. In the face of uncertainty about the law of distribution of time of occurrence of failures due to small amounts of statistical data, which usually happens in the initial stages of technology development, the researcher has to decide on the choice of prior model reliability based on previous operating experience of prototypes or analogues. Systematization of information on the practical use of basic distributions in forecasting and assessing the reliability of various technical systems is an important scientific task.

In the above material is the systematization of the information published in literature, and representing the analysis results of model and experimental studies of reliability of equipment, as well as statistical data obtained during operation.

Presents theoretical information on the use of gamma distribution in the theory of reliability can be used as a first approximation and is subject to obligatory specification, using different criteria of testing hypotheses, increasing the volume of statistical data in subsequent tests.

It is necessary to have sufficient grounds for application of exponential distribution law, like any other. Therefore, the article may be useful for researchers in the early stages of development or modernization of technical systems, as a priori information to build the models and criteria used to ensure and control the reliability.

Ключевые слова: надежность, распределение, наработка, вероятность, плотность, этап, математическое ожидание.

Keywords: reliability, distribution, operation time, probability, density of distribution, stage, expected value.

Для описания отказов системы могут быть предложены модели, предназначенные для решения различных задач надежности и по-разному учитывающие комплекс факторов, присущих характеру отказов.

Случайный характер возникновения отказов в процессе эксплуатации технических систем и их элементов позволяет применять в их описании вероятностно-статистические методы. Наиболее распространенными являются модели отказов, основанные на распределении соответствующих случайных величин – наработок до отказа невосстанавливаемых объектов и наработок между отказами восстанавливаемых объектов.

В качестве основных видов распределения наработок изделий до отказа следует выделить :

• экспоненциальное;
• Вейбулла-Гнеденко;
• гамма;
• логарифмически-нормальное;
• нормальное.

В результате обзора литературы в области надежности технических систем дана оценка практического применения гамма-распределения при исследовании различных технических объектов. На основе проведенного анализа можно подобрать подходящее априорное распределение соответствующего критерия или показателя надежности.

Гамма-распределение имеет двухпараметрическую плотность с параметром формы и параметром масштаба :

.

Вероятность безотказной работы определяется по формуле:

,

где: – гамма-функция;

– неполная гамма-функция.

Математическое ожидание (среднее время безотказной работы) и среднее квадратическое отклонение для гамма-распределения равны:

.

Формула для интенсивности отказов следующая:

.

Гамма-распределение служит для описания износовых отказов; отказов вследствие накопления повреждений; описания наработки сложной технической системы с резервными элементами; распределения времени восстановления ; а также может быть использовано при рассмотрении долговечности (ресурса) некоторых технических объектов .

Гамма-распределение обладает рядом полезных свойств:

На основании вышесказанного можно сделать вывод, что гамма-распределение допустимо использовать на всех участках жизненного цикла: приработки (), нормальной эксплуатации () и старения () .

Исходя из , в задачах, которые решаются в терминах преобразования Лапласа, гамма-распределением удобно аппроксимировать реальные распределения.

В приводится следующее определение: гамма-распределение – характеристика времени возникновения отказов в сложных электромеханических системах в тех случаях, когда имеют место мгновенные отказы элементов на начальной стадии эксплуатации или в процессе отладки системы, то есть является удобной характеристикой времени возникновения отказов аппаратуры в процессе ее приработки.

Для сложных технических систем, состоящих из элементов, у которых вероятность безотказной работы имеет показательное распределение, вероятность безотказной работы системы в целом будет иметь гамма-распределение.

Распределение времени возникновения отказов сложной технической системы с резервом замещением (при условии, что потоки отказов основной системы и всех резервных простейшие) также может быть описано гамма-распределением . Аналогичным образом в случае ненагруженного или смешанного резервирования вероятность безотказной работы системы подчиняется обобщенному гамма-распределению.

В заключение необходимо отметить, что при решении отдельных задач также применяют специальные виды (их несколько десятков), а также дискретные распределения, которые в рамках данной статьи не рассматривались. При этом между распределениями существуют различные взаимные переходы и связи. Несмотря на существующие критерии согласия выбранного теоретического и эмпирического распределения, они все дают ответ на вопрос: есть или нет достаточно серьезных оснований отвергнуть гипотезу о выбранном распределении? Авторами замечено, что любые данные можно подогнать под многопараметрический закон, даже если он не будет соответствовать реальным физическим явлениям . Таким образом, при выборе вида распределения и его параметров необходимо прежде всего учитывать физическую сущность происходящих процессов и событий.

Список литературы:

1. ГОСТ Р.27.001-2009. Надежность в технике. Модели отказов. – М.: Стандартинформ, 2010. – 16 с.
2. Герцбах И.Б., Кордонский Х.Б. Модели отказов / под ред. Б.В. Гнеденко. – М.: Советское радио, 1966. – 166 с.
3. Гнеденко Б.В. Вопросы математической теории надежности. – М.: Радио и связь,1983. – 376 с.
4. Каштанов В.Н., Медведев А.И. Теория надежности сложных систем: уч.пособие – М.: ФИЗМАТЛИТ, 2010. – 609 с.
5. Литвиненко Р.С. Имитационная модель процесса функционирования электротехнического комплекса с учетом надежности его элементов // Журнал «Надежность». – 2016. – № 1 (56) – С. 46–54.
6. Литвиненко Р.С., Идиятуллин Р.Г., Киснеева Л.Н. Оценка надежности гибридного транспортного средства на этапе разработки // Журнал «Транспорт: наука, техника, управление». – 2016. – № 2 – С. 34–40.
7. Машиностроение: энциклопедия в 40 т. Т. IV-3: Надежность машин / В.В. Клюев, В.В. Болотин, Ф.Р. Соснин и др.; под общ. ред. В.В. Клюева. – М.: Машиностроение, 2003. – 592 с.
8. Труханов В.М. Надежность технических систем типа подвижных установок на этапе проектирования и испытания опытных образцов: научное издание – М.: Машиностроение, 2003. – 320 с.
9. Хазов Б.Ф., Дидусев Б.А. Справочник по расчету надежности машин на стадии проектирования. – М.: Машиностроение, 1986. – 224 с.
10. Черкесов Г.Н. Надежность аппаратно-программных комплексов: учеб. пособие. – СПб.: Питер, 2005. – 479 с.

В этой статье описаны синтаксис формулы и использование функции ГАММА.РАСПП в Microsoft Excel.

Возвращает гамма-распределение. Эту функцию можно использовать для изучения переменных, которые имеют асимметричное распределение. Гамма-распределение широко используется при анализе систем массового обслуживания.

Синтаксис

ГАММА.РАСП(x;альфа;бета;интегральная)

Аргументы функции ГАММА.РАСП описаны ниже.

x - обязательный аргумент. Значение, для которого требуется вычислить распределение.

Альфа - обязательный аргумент. Параметр распределения.

Бета - обязательный аргумент. Параметр распределения. Если аргумент "бета" = 1, функция ГАММА.РАСП возвращает стандартное гамма-распределение.

Интегральная - обязательный аргумент. Логическое значение, определяющее форму функции. Если аргумент "интегральная" имеет значение ИСТИНА, функция ГАММА.РАСП возвращает интегральную функцию распределения; если этот аргумент имеет значение ЛОЖЬ, возвращается функция плотности распределения вероятности.

Замечания

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем - клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные	Описание
	Значение, для которого требуется вычислить распределение
	Параметр распределения альфа
	Параметр распределения бета
Формула	Описание	Результат
ГАММА.РАСП(A2;A3;A4;ЛОЖЬ)	Плотность вероятности при использовании значений x, альфа и бета в ячейках A2, A3, A4 с интегральным аргументом ЛОЖЬ.
ГАММА.РАСП(A2;A3;A4;ИСТИНА)	Интегральное распределение при использовании значений x, альфа и бета в ячейках A2, A3, A4 с интегральным аргументом ИСТИНА.