Resuelve la ecuación en pasos. Resolver la ecuación con fracciones en línea. Resolver ejemplos reales de ecuaciones lineales simples

En este video, vamos a echar un vistazo a todo el conjunto. ecuaciones lineales, que se resuelven con el mismo algoritmo, por eso se llaman los más simples.

Para empezar, definamos: ¿qué es una ecuación lineal y cuál de ellas debería llamarse la más simple?

Una ecuación lineal es aquella en la que solo hay una variable, y solo en primer grado.

La ecuación más simple significa la construcción:

Todas las demás ecuaciones lineales se reducen a las más simples usando el algoritmo:

1. Abra los corchetes, si los hubiere;
2. Mueva los términos que contienen una variable a un lado del signo igual y los términos sin variable al otro;
3. Traiga términos similares a la izquierda y derecha del signo igual;
4. Divide la ecuación resultante por el coeficiente de la variable $x$ .

Por supuesto, este algoritmo no siempre ayuda. El caso es que a veces, después de todas estas maquinaciones, el coeficiente de la variable $x$ resulta ser igual a cero. En este caso, dos opciones son posibles:

1. La ecuación no tiene soluciones en absoluto. Por ejemplo, cuando obtienes algo como $0\cdot x=8$, es decir a la izquierda es cero, y a la derecha es un número distinto de cero. En el video a continuación, veremos varias razones por las que esta situación es posible.
2. La solución son todos los números. El único caso en que esto es posible es cuando la ecuación se ha reducido a la construcción $0\cdot x=0$. Es bastante lógico que no importa qué $x$ sustituyamos, seguirá resultando que "cero es igual a cero", es decir igualdad numérica correcta.

Y ahora veamos cómo funciona todo en el ejemplo de problemas reales.

Ejemplos de resolución de ecuaciones

Hoy tratamos con ecuaciones lineales, y solo con las más simples. En general, una ecuación lineal significa cualquier igualdad que contiene exactamente una variable, y llega solo al primer grado.

Tales construcciones se resuelven aproximadamente de la misma manera:

1. En primer lugar, debe abrir los paréntesis, si los hay (como en nuestro último ejemplo);
2. Entonces trae similares
3. Finalmente, aísle la variable, es decir todo lo que está conectado con la variable, los términos en los que está contenida, se transfiere a un lado, y todo lo que queda sin ella se transfiere al otro lado.

Luego, como regla, debe traer similar a cada lado de la igualdad resultante, y luego solo queda dividir por el coeficiente en "x", y obtendremos la respuesta final.

En teoría, esto parece agradable y simple, pero en la práctica, incluso los estudiantes de secundaria experimentados pueden cometer errores ofensivos en ecuaciones lineales bastante simples. Por lo general, se cometen errores al abrir corchetes o al contar "más" y "menos".

Además, sucede que una ecuación lineal no tiene solución alguna, o que la solución es toda la recta numérica, es decir cualquier número. Analizaremos estas sutilezas en la lección de hoy. Pero comenzaremos, como ya entendiste, con lo más tareas simples.

Esquema para resolver ecuaciones lineales simples

Para empezar, permítanme una vez más escribir el esquema completo para resolver las ecuaciones lineales más simples:

1. Expanda los paréntesis, si los hay.
2. Aislar variables, es decir todo lo que contiene "x" se transfiere a un lado, y sin "x", al otro.
3. Presentamos términos similares.
4. Dividimos todo por el coeficiente en "x".

Por supuesto, este esquema no siempre funciona, tiene ciertas sutilezas y trucos, y ahora los conoceremos.

Resolver ejemplos reales de ecuaciones lineales simples

Tarea 1

En el primer paso, estamos obligados a abrir los corchetes. Pero no están en este ejemplo, así que nos saltamos este paso. En el segundo paso, necesitamos aislar las variables. Tenga en cuenta: estamos hablando solo de términos individuales. Vamos a escribir:

Damos términos similares a la izquierda ya la derecha, pero esto ya se ha hecho aquí. Por lo tanto, procedemos al cuarto paso: dividir por un factor:

\[\frac(6x)(6)=-\frac(72)(6)\]

Aquí tenemos la respuesta.

Tarea 2

En esta tarea, podemos observar los paréntesis, así que ampliémoslos:

Tanto a la izquierda como a la derecha, vemos aproximadamente la misma construcción, pero actuemos de acuerdo con el algoritmo, es decir. secuestrar variables:

Aquí hay algunos como:

¿En qué raíces funciona esto? Respuesta: para cualquiera. Por lo tanto, podemos escribir que $x$ es cualquier número.

Tarea #3

La tercera ecuación lineal ya es más interesante:

\[\left(6-x \right)+\left(12+x \right)-\left(3-2x \right)=15\]

Aquí hay varios corchetes, pero no se multiplican por nada, solo tienen diferentes signos delante de ellos. Vamos a desglosarlos:

Realizamos el segundo paso ya conocido por nosotros:

\[-x+x+2x=15-6-12+3\]

Calculemos:

Realizamos el último paso: dividimos todo por el coeficiente en "x":

\[\frac(2x)(x)=\frac(0)(2)\]

Cosas para recordar al resolver ecuaciones lineales

Si ignoramos tareas demasiado simples, me gustaría decir lo siguiente:

• Como dije anteriormente, no todas las ecuaciones lineales tienen una solución, a veces simplemente no hay raíces;
• Incluso si hay raíces, cero puede entrar entre ellas, no hay nada de malo en eso.

Cero es el mismo número que el resto, no debes discriminarlo de alguna manera o asumir que si obtienes cero, entonces hiciste algo mal.

Otra característica está relacionada con la expansión de los paréntesis. Tenga en cuenta: cuando hay un "menos" delante de ellos, lo eliminamos, pero entre paréntesis cambiamos los signos a opuesto. Y luego podemos abrirlo de acuerdo con los algoritmos estándar: obtendremos lo que vimos en los cálculos anteriores.

entender esto hecho simple evitará que cometas errores estúpidos e hirientes en la escuela secundaria cuando se da por hecho que se hacen esas cosas.

Resolver ecuaciones lineales complejas

Pasemos a ecuaciones más complejas. Ahora los diseños se volverán más complejos y cuando se ejecuten varias transformaciones habrá una función cuadrática. Sin embargo, no debe tener miedo de esto, porque si, de acuerdo con la intención del autor, resolvemos una ecuación lineal, en el proceso de transformación, todos los monomios que contienen una función cuadrática necesariamente se reducirán.

Ejemplo 1

Obviamente, el primer paso es abrir los corchetes. Hagamos esto con mucho cuidado:

Ahora tomemos la privacidad:

\[-x+6((x)^(2))-6((x)^(2))+x=-12\]

Aquí hay algunos como:

Obviamente, esta ecuación no tiene soluciones, por lo que en la respuesta escribimos lo siguiente:

\[\variedad \]

o sin raíces.

Ejemplo #2

Realizamos los mismos pasos. Primer paso:

Movamos todo con una variable a la izquierda, y sin ella, a la derecha:

Aquí hay algunos como:

Obviamente, esta ecuación lineal no tiene solución, por lo que la escribimos así:

\[\varnada\],

o sin raíces.

Matices de la solución.

Ambas ecuaciones están completamente resueltas. En el ejemplo de estas dos expresiones, una vez más nos aseguramos de que incluso en las ecuaciones lineales más simples, todo puede no ser tan simple: puede haber uno, o ninguno, o infinitamente muchos. En nuestro caso, consideramos dos ecuaciones, en ambas simplemente no hay raíces.

Pero me gustaría llamar su atención sobre otro hecho: cómo trabajar con corchetes y cómo expandirlos si hay un signo menos delante de ellos. Considere esta expresión:

Antes de abrir, debe multiplicar todo por "x". Tenga en cuenta: multiplicar cada término individual. Dentro hay dos términos - respectivamente, dos términos y se multiplica.

Y solo después de que se hayan completado estas transformaciones aparentemente elementales, pero muy importantes y peligrosas, se puede abrir el paréntesis desde el punto de vista de que hay un signo menos después. Sí, sí: solo que ahora, cuando se realizan las transformaciones, recordamos que hay un signo menos delante de los corchetes, lo que significa que todo lo que está debajo solo cambia de signo. Al mismo tiempo, los corchetes desaparecen y, lo que es más importante, también desaparece el "menos" frontal.

Hacemos lo mismo con la segunda ecuación:

No es casualidad que preste atención a estos pequeños hechos aparentemente insignificantes. Porque resolver ecuaciones siempre es una secuencia de transformaciones elementales, donde la incapacidad de realizar acciones simples de manera clara y competente lleva al hecho de que los estudiantes de secundaria vienen a mí y aprenden a resolver ecuaciones tan simples nuevamente.

Por supuesto, llegará el día en que perfeccionarás estas habilidades hasta el automatismo. Ya no tendrás que realizar tantas transformaciones cada vez, escribirás todo en una sola línea. Pero mientras está aprendiendo, necesita escribir cada acción por separado.

Resolver ecuaciones lineales aún más complejas

Lo que vamos a resolver ahora difícilmente puede llamarse la tarea más simple, pero el significado sigue siendo el mismo.

Tarea 1

\[\left(7x+1 \right)\left(3x-1 \right)-21((x)^(2))=3\]

Multipliquemos todos los elementos de la primera parte:

Hagamos un retiro:

Aquí hay algunos como:

Hagamos el último paso:

\[\frac(-4x)(4)=\frac(4)(-4)\]

Aquí está nuestra respuesta final. Y, a pesar de que en el proceso de resolución teníamos coeficientes con una función cuadrática, sin embargo, se cancelaron mutuamente, lo que hace que la ecuación sea exactamente lineal, no cuadrada.

Tarea 2

\[\left(1-4x \right)\left(1-3x \right)=6x\left(2x-1 \right)\]

Hagamos el primer paso con cuidado: multiplique cada elemento del primer paréntesis por cada elemento del segundo. En total, se deben obtener cuatro nuevos términos después de las transformaciones:

Y ahora realiza con cuidado la multiplicación en cada término:

Movamos los términos con "x" a la izquierda y sin - a la derecha:

\[-3x-4x+12((x)^(2))-12((x)^(2))+6x=-1\]

Aquí hay términos similares:

Hemos recibido una respuesta definitiva.

Matices de la solución.

La observación más importante sobre estas dos ecuaciones es esta: tan pronto como comenzamos a multiplicar paréntesis en los que hay más de un término, esto se hace de acuerdo con la siguiente regla: tomamos el primer término del primero y multiplicamos con cada elemento del segundo; luego tomamos el segundo elemento del primero y lo multiplicamos de manera similar con cada elemento del segundo. Como resultado, obtenemos cuatro términos.

Sobre la suma algebraica

Con el último ejemplo, me gustaría recordarles a los estudiantes qué es una suma algebraica. En matemáticas clásicas, por $1-7$ nos referimos a una construcción simple: restamos siete de uno. En álgebra, queremos decir con esto lo siguiente: al número "uno" le agregamos otro número, a saber, "menos siete". Esta suma algebraica difiere de la suma aritmética habitual.

Tan pronto como al realizar todas las transformaciones, cada suma y multiplicación, comience a ver construcciones similares a las descritas anteriormente, simplemente no tendrá ningún problema en álgebra cuando trabaje con polinomios y ecuaciones.

En conclusión, veamos un par de ejemplos más que serán aún más complejos que los que acabamos de ver, y para resolverlos, tendremos que expandir ligeramente nuestro algoritmo estándar.

Resolver ecuaciones con una fracción

Para resolver tales tareas, habrá que añadir un paso más a nuestro algoritmo. Pero primero, recordaré nuestro algoritmo:

1. Abra los paréntesis.
2. Variables separadas.
3. Trae similares.
4. Dividir por un factor.

Por desgracia, este maravilloso algoritmo, con toda su eficiencia, no es del todo apropiado cuando tenemos fracciones frente a nosotros. Y en lo que veremos a continuación, tenemos una fracción a la izquierda y a la derecha en ambas ecuaciones.

¿Cómo trabajar en este caso? ¡Sí, es muy simple! Para hacer esto, debe agregar un paso más al algoritmo, que se puede realizar tanto antes como después de la primera acción, es decir, para deshacerse de las fracciones. Así, el algoritmo será el siguiente:

1. Deshazte de las fracciones.
2. Abra los paréntesis.
3. Variables separadas.
4. Trae similares.
5. Dividir por un factor.

¿Qué significa "deshacerse de las fracciones"? ¿Y por qué es posible hacer esto antes y después del primer paso estándar? De hecho, en nuestro caso, todas las fracciones son numéricas en términos del denominador, es decir en todas partes el denominador es solo un número. Por lo tanto, si multiplicamos ambas partes de la ecuación por este número, nos desharemos de las fracciones.

Ejemplo 1

\[\frac(\left(2x+1 \right)\left(2x-3 \right))(4)=((x)^(2))-1\]

Eliminemos las fracciones en esta ecuación:

\[\frac(\left(2x+1 \right)\left(2x-3 \right)\cdot 4)(4)=\left(((x)^(2))-1 \right)\cdot 4\]

Tenga en cuenta: todo se multiplica por "cuatro" una vez, es decir el hecho de que tenga dos corchetes no significa que tenga que multiplicar cada uno de ellos por "cuatro". Vamos a escribir:

\[\left(2x+1 \right)\left(2x-3 \right)=\left(((x)^(2))-1 \right)\cdot 4\]

Ahora vamos a abrirlo:

Realizamos la reclusión de una variable:

Realizamos la reducción de plazos similares:

\[-4x=-1\izquierda| :\izquierda(-4 \derecha) \derecha.\]

\[\frac(-4x)(-4)=\frac(-1)(-4)\]

Hemos recibido la solución final, pasamos a la segunda ecuación.

Ejemplo #2

\[\frac(\left(1-x \right)\left(1+5x \right))(5)+((x)^(2))=1\]

Aquí realizamos todas las mismas acciones:

\[\frac(\left(1-x \right)\left(1+5x \right)\cdot 5)(5)+((x)^(2))\cdot 5=5\]

\[\frac(4x)(4)=\frac(4)(4)\]

Problema resuelto.

Eso, de hecho, es todo lo que quería contar hoy.

Puntos clave

Los hallazgos clave son los siguientes:

• Conocer el algoritmo para la resolución de ecuaciones lineales.
• Posibilidad de abrir corchetes.
• No te preocupes si en algún lugar tienes funciones cuadráticas, muy probablemente, en el proceso de nuevas transformaciones, se reducirán.
• Las raíces en las ecuaciones lineales, incluso las más simples, son de tres tipos: una sola raíz, toda la recta numérica es una raíz, no hay ninguna raíz.

Espero que esta lección lo ayude a dominar un tema simple pero muy importante para una mayor comprensión de todas las matemáticas. Si algo no está claro, vaya al sitio, resuelva los ejemplos presentados allí. ¡Estén atentos, hay muchas más cosas interesantes esperando por ustedes!

La calculadora de fracciones en línea le permite producir la más simple operaciones aritmeticas con fracciones: suma de fracciones, resta de fracciones, multiplicación de fracciones, división de fracciones. Para hacer cálculos, llena los campos correspondientes a los numeradores y denominadores de dos fracciones.

Fracción en matemáticas se llama un número que representa una parte de una unidad o varias de sus partes.

Una fracción común se escribe como dos números, generalmente separados por una línea horizontal, que indica el signo de división. El número arriba de la barra se llama numerador. El número debajo de la barra se llama denominador. El denominador de una fracción muestra el número de partes iguales en que se divide el todo, y el numerador de la fracción muestra el número de estas partes del todo tomadas.

Las fracciones son correctas e incorrectas.

• Una fracción correcta es aquella cuyo numerador es menor que el denominador.
• Una fracción impropia es cuando el numerador es mayor que el denominador.

Una fracción mixta es una fracción escrita como un número entero y una fracción propia, y se entiende como la suma de este número y la parte fraccionaria. En consecuencia, una fracción que no tiene una parte entera se llama fracción simple. Cualquier fracción mixta se puede convertir en una fracción simple impropia.

Para convertir una fracción mixta en una ordinaria, es necesario sumar el producto de la parte entera y el denominador al numerador de la fracción:

Cómo convertir una fracción ordinaria a una mixta

Para poder traducir fracción común en mixto, es necesario:

1. Dividir el numerador de una fracción por su denominador
2. El resultado de la división será la parte entera
3. El resto de la rama será el numerador.

Cómo convertir una fracción común a un decimal

Para convertir una fracción a decimal, necesitas dividir su numerador por el denominador.

Para poder traducir decimal en lo ordinario, es necesario:

Cómo convertir una fracción a un porcentaje

Para convertir una fracción ordinaria o mixta en un porcentaje, debe convertirla en una fracción decimal y multiplicarla por 100.

Cómo convertir porcentajes a fracciones

Para convertir porcentajes a fracciones, es necesario obtener una fracción decimal a partir de porcentajes (dividiendo por 100), luego convertir la fracción decimal resultante a una ordinaria.

Suma de fracciones

El algoritmo para sumar dos fracciones es el siguiente:

1. Sumar fracciones sumando sus numeradores.

Resta de fracciones

Algoritmo de acciones al restar dos fracciones:

1. Traducir fracciones mixtas en ordinarios (deshágase de toda la parte).
2. Trae fracciones a común denominador. Para hacer esto, necesitas multiplicar el numerador y el denominador de la primera fracción por el denominador de la segunda fracción, y multiplicar el numerador y el denominador de la segunda fracción por el denominador de la primera fracción.
3. Resta una fracción de otra restando el numerador de la segunda fracción del numerador de la primera.
4. Encuentra el máximo común divisor (MCD) del numerador y el denominador y reduce la fracción dividiendo el numerador y el denominador por el MCD.
5. Si el numerador de la fracción final es mayor que el denominador, seleccione la parte entera.

Multiplicación de fracciones

Algoritmo de acciones al multiplicar dos fracciones:

1. Convierta fracciones mixtas en fracciones comunes (deshágase de la parte entera).
2. Encuentra el máximo común divisor (MCD) del numerador y el denominador y reduce la fracción dividiendo el numerador y el denominador por el MCD.
3. Si el numerador de la fracción final es mayor que el denominador, seleccione la parte entera.

división de fracciones

Algoritmo de acciones al dividir dos fracciones:

1. Convierta fracciones mixtas en fracciones comunes (deshágase de la parte entera).
2. Para dividir fracciones, debe convertir la segunda fracción intercambiando su numerador y denominador, y luego multiplicar las fracciones.
3. Multiplica el numerador de la primera fracción por el numerador de la segunda fracción y el denominador de la primera fracción por el denominador de la segunda.
4. Encuentra el máximo común divisor (MCD) del numerador y el denominador y reduce la fracción dividiendo el numerador y el denominador por el MCD.
5. Si el numerador de la fracción final es mayor que el denominador, seleccione la parte entera.

Calculadoras y conversores en línea:

Una ecuación con una incógnita que, después de abrir los paréntesis y reducir los términos semejantes, toma la forma

hacha + b = 0, donde a y b son números arbitrarios, se llama ecuación lineal con una desconocida. Hoy descubriremos cómo resolver estas ecuaciones lineales.

Por ejemplo, todas las ecuaciones:

2x + 3 \u003d 7 - 0.5x; 0,3x = 0; x / 2 + 3 \u003d 1/2 (x - 2) - lineal.

El valor de la incógnita que convierte la ecuación en una verdadera igualdad se llama decisión o la raíz de la ecuación .

Por ejemplo, si en la ecuación 3x + 7 \u003d 13 sustituimos el número 2 en lugar de la incógnita x, entonces obtenemos la igualdad correcta 3 2 + 7 \u003d 13. Por lo tanto, el valor x \u003d 2 es la solución o la raíz de la ecuación.

Y el valor x \u003d 3 no convierte la ecuación 3x + 7 \u003d 13 en una verdadera igualdad, ya que 3 2 + 7 ≠ 13. Por lo tanto, el valor x \u003d 3 no es una solución o una raíz de la ecuación.

La solución de cualquier ecuación lineal se reduce a la solución de ecuaciones de la forma

hacha + b = 0.

Transferimos el término libre del lado izquierdo de la ecuación al lado derecho, mientras cambiamos el signo frente a b al opuesto, obtenemos

Si a ≠ 0, entonces x = – b/a .

Ejemplo 1 Resuelve la ecuación 3x + 2 =11.

Pasamos 2 del lado izquierdo de la ecuación a la derecha, mientras cambiamos el signo frente a 2 al opuesto, obtenemos
3x \u003d 11 - 2.

Hagamos la resta, entonces
3x = 9.

Para encontrar x, necesitas dividir el producto por un factor conocido, es decir,
x = 9:3.

Entonces el valor x = 3 es la solución o la raíz de la ecuación.

Respuesta: x = 3.

Si a = 0 y b = 0, luego obtenemos la ecuación 0x \u003d 0. Esta ecuación tiene infinitas soluciones, ya que al multiplicar cualquier número por 0, obtenemos 0, pero b también es 0. La solución a esta ecuación es cualquier número.

Ejemplo 2 Resuelve la ecuación 5(x - 3) + 2 = 3 (x - 4) + 2x - 1.

Expandamos los paréntesis:
5x - 15 + 2 \u003d 3x - 12 + 2x - 1.

5x - 3x - 2x \u003d - 12 - 1 + 15 - 2.

Aquí hay miembros similares:
0x = 0.

respuesta: x es cualquier numero.

Si a = 0 y b ≠ 0, entonces obtenemos la ecuación 0x = - b. Esta ecuación no tiene solución, ya que al multiplicar cualquier número por 0, obtenemos 0, pero b ≠ 0.

Ejemplo 3 Resuelve la ecuación x + 8 = x + 5.

Agrupemos los términos que contienen incógnitas en el lado izquierdo y los términos libres en el lado derecho:
x - x \u003d 5 - 8.

Aquí hay miembros similares:
0x = - 3.

Respuesta: no hay soluciones.

En Figura 1 se muestra el esquema para resolver la ecuación lineal

Compongamos un esquema general para resolver ecuaciones con una variable. Considere la solución del ejemplo 4.

Ejemplo 4 Resolvamos la ecuación

1) Multiplica todos los términos de la ecuación por el mínimo común múltiplo de los denominadores, igual a 12.

2) Después de la reducción obtenemos
4 (x - 4) + 3 2 (x + 1) - 12 = 6 5 (x - 3) + 24x - 2 (11x + 43)

3) Para separar los miembros que contienen miembros desconocidos y libres, abra los corchetes:
4x - 16 + 6x + 6 - 12 \u003d 30x - 90 + 24x - 22x - 86.

4) Agrupamos en una parte los términos que contienen incógnitas y en la otra los términos libres:
4x + 6x - 30x - 24x + 22x \u003d - 90 - 86 + 16 - 6 + 12.

5) Aquí hay miembros similares:
- 22x = - 154.

6) Dividir por - 22, Obtenemos
x = 7.

Como puedes ver, la raíz de la ecuación es siete.

En general, tal Las ecuaciones se pueden resolver de la siguiente manera.:

a) llevar la ecuación a una forma entera;

b) corchetes abiertos;

c) agrupar los términos que contienen la incógnita en una parte de la ecuación y los términos libres en la otra;

d) traer miembros similares;

e) resolver una ecuación de la forma aх = b, que se obtuvo después de traer términos semejantes.

Sin embargo, este esquema no es necesario para todas las ecuaciones. Al resolver muchas ecuaciones más simples, uno tiene que empezar no desde la primera, sino desde la segunda ( Ejemplo. 2), tercero ( Ejemplo. 13) e incluso desde la quinta etapa, como en el ejemplo 5.

Ejemplo 5 Resuelve la ecuación 2x ​​= 1/4.

Encontramos la incógnita x \u003d 1/4: 2,
X = 1/8 .

Considere la solución de algunas ecuaciones lineales encontradas en el examen de estado principal.

Ejemplo 6 Resuelve la ecuación 2 (x + 3) = 5 - 6x.

2x + 6 = 5 - 6x

2x + 6x = 5 - 6

Respuesta: - 0.125

Ejemplo 7 Resuelva la ecuación - 6 (5 - 3x) \u003d 8x - 7.

– 30 + 18x = 8x – 7

18x - 8x = - 7 +30

Respuesta: 2.3

Ejemplo 8 Resuelve la ecuación

3(3x - 4) = 4 7x + 24

9x - 12 = 28x + 24

9x - 28x = 24 + 12

Ejemplo 9 Encuentre f(6) si f (x + 2) = 3 7

Solución

Como necesitamos encontrar f(6), y sabemos f (x + 2),
entonces x + 2 = 6.

Resolvemos la ecuación lineal x + 2 = 6,
obtenemos x \u003d 6 - 2, x \u003d 4.

Si x = 4 entonces
f(6) = 3 7-4 = 3 3 = 27

Respuesta: 27.

Si todavía tiene preguntas, desea tratar la solución de ecuaciones más a fondo, regístrese en mis lecciones en el HORARIO. ¡Estaré encantado de ayudarle!

TutorOnline también recomienda ver un nuevo video tutorial de nuestra tutora Olga Alexandrovna, que te ayudará a comprender tanto las ecuaciones lineales como otras.

sitio, con copia total o parcial del material, se requiere un enlace a la fuente.

¿Qué son las ecuaciones irracionales y cómo resolverlas?

Las ecuaciones en las que la variable está contenida bajo el signo de radical o bajo el signo de elevar a una potencia fraccionaria se denominan irracional. Cuando tratamos con una potencia fraccionaria, nos privamos de muchas operaciones matemáticas para resolver la ecuación, por lo que las ecuaciones irracionales se resuelven de una manera especial.

Las ecuaciones irracionales generalmente se resuelven elevando ambos lados de la ecuación a la misma potencia. Al mismo tiempo, elevar ambas partes de la ecuación a la misma potencia impar es una transformación equivalente de la ecuación, y a uno par no es equivalente. Tal diferencia se obtiene debido a tales características de exponenciación, como si se elevara a una potencia par, entonces valores negativos"perdido".

El objetivo de elevar ambos lados de una ecuación irracional a una potencia es deshacerse de la "irracionalidad". Por lo tanto, necesitamos elevar ambas partes de la ecuación irracional a tal grado que todas las potencias fraccionarias de ambas partes de la ecuación se conviertan en números enteros. Luego se puede buscar una solución a esta ecuación, la cual coincidirá con las soluciones de la ecuación irracional, con la diferencia que en el caso de elevar a una potencia par, se pierde el signo y las soluciones finales requerirán verificación y no todo funcionará.

Por lo tanto, la principal dificultad está asociada con elevar ambas partes de la ecuación a la misma potencia par: debido a la no equivalencia de la transformación, pueden aparecer raíces extrañas. Por lo tanto, es obligatorio verificar todas las raíces encontradas. La verificación de las raíces encontradas es olvidada con mayor frecuencia por aquellos que deciden ecuación irracional. Tampoco siempre está claro hasta qué punto es necesario plantear una ecuación irracional para deshacerse de la irracionalidad y resolverla. Nuestra calculadora inteligente está diseñada para resolver una ecuación irracional y verificar automáticamente todas las raíces, lo que eliminará el olvido.

Calculadora online gratuita de ecuaciones irracionales

Nuestro solucionador gratuito le permitirá resolver una ecuación irracional en línea de cualquier complejidad en cuestión de segundos. Todo lo que necesita hacer es ingresar sus datos en la calculadora. También puedes aprender a resolver la ecuación en nuestro sitio web. Y si tiene alguna pregunta, puede hacerla en nuestro grupo VKontakte.

Asignación de servicios. La calculadora matricial está diseñada para resolver sistemas de ecuaciones lineales de forma matricial (ver un ejemplo de resolución de problemas similares).

Instrucción. Para una solución en línea, debe seleccionar el tipo de ecuación y establecer la dimensión de las matrices correspondientes. donde A, B, C son matrices dadas, X es la matriz deseada. Las ecuaciones matriciales de la forma (1), (2) y (3) se resuelven mediante la matriz inversa A -1 . Si se da la expresión A X - B = C, entonces es necesario primero sumar las matrices C + B y encontrar una solución para la expresión A X = D , donde D = C + B . Si se da la expresión A*X = B 2, entonces primero se debe elevar al cuadrado la matriz B.

También se recomienda familiarizarse con las operaciones básicas sobre matrices.

Ejemplo 1. Ejercicio. Encontrar una solución a una ecuación matricial
Solución. Denotar:
Entonces la ecuación matricial se escribirá de la forma: A·X·B = C.
El determinante de la matriz A es detA=-1
Como A es una matriz no singular, existe una matriz inversa A -1 . Multiplica ambos lados de la ecuación de la izquierda por A -1: Multiplica ambos lados de esta ecuación de la izquierda por A -1 y de la derecha por B -1: A -1 A X B B -1 = A -1 C B -1 . Como A A -1 = B B -1 = E y E X = X E = X, entonces X = A -1 C B -1

matriz inversa A-1:
Encuentre la matriz inversa B -1 .
Transponer matriz B T:
Matriz inversa B -1:
Buscamos la matriz X por la fórmula: X = A -1 C B -1

Respuesta:

Ejemplo #2. Ejercicio. Resolver ecuación matricial
Solución. Denotar:
Entonces la ecuación matricial se escribirá en la forma: A X = B.
El determinante de la matriz A es detA=0
Como A es una matriz degenerada (el determinante es 0), la ecuación no tiene solución.

Ejemplo #3. Ejercicio. Encontrar una solución a una ecuación matricial
Solución. Denotar:
Entonces la ecuación matricial se escribirá de la forma: X·A = B.
El determinante de la matriz A es detA=-60
Como A es una matriz no singular, existe una matriz inversa A -1 . Multiplica a la derecha ambos lados de la ecuación por A -1: X A A -1 = B A -1 , de donde encontramos que X = B A -1
Encuentre la matriz inversa A -1 .
Matriz traspuesta A T: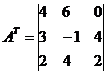
Matriz inversa A -1:
Buscamos la matriz X por la fórmula: X = B A -1


Respuesta: >