» Statistics

Statistics and data processing in psychology
(continuation)

Correlation analysis

When studying correlations tries to determine whether there is any relationship between two indicators in the same sample (for example, between the height and weight of children or between the level of IQ and school performance) or between two different samples (for example, when comparing pairs of twins), and if this relationship exists, then whether an increase in one indicator is accompanied by an increase (positive correlation) or a decrease (negative correlation) in the other.

In other words, correlation analysis helps to establish whether it is possible to predict the possible values ​​of one indicator, knowing the value of another.

Until now, when analyzing the results of our experience in studying the effects of marijuana, we have deliberately ignored such an indicator as reaction time. Meanwhile, it would be interesting to check whether there is a connection between the effectiveness of reactions and their speed. This would allow, for example, to assert that the slower a person is, the more accurate and efficient his actions will be and vice versa.

For this purpose, two different methods can be used: the parametric method of calculating the Bravais-Pearson coefficient (r) and the calculation of the Spearman rank correlation coefficient (r s), which is applied to ordinal data, i.e. is nonparametric. However, let’s first understand what a correlation coefficient is.

Correlation coefficient

The correlation coefficient is a value that can vary from +1 to -1. In the case of a complete positive correlation, this coefficient is equal to plus 1, and in the case of a completely negative correlation, it is minus 1. On the graph, this corresponds to a straight line passing through the intersection points of the values ​​of each pair of data:

If these points do not line up in a straight line, but form a “cloud,” the correlation coefficient in absolute value becomes less than one and, as this cloud is rounded, approaches zero:

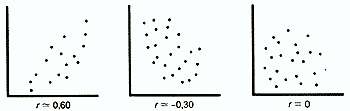
If the correlation coefficient is 0, both variables are completely independent of each other.

In the humanities, a correlation is considered strong if its coefficient is greater than 0.60; if it exceeds 0.90, then the correlation is considered very strong. However, in order to be able to draw conclusions about the relationships between variables, the sample size is of great importance: the larger the sample, the more reliable the value of the obtained correlation coefficient. There are tables with critical values ​​of the Bravais-Pearson and Spearman correlation coefficient for different numbers of degrees of freedom (it is equal to the number of pairs minus 2, i.e. n- 2). Only if the correlation coefficients are greater than these critical values ​​can they be considered reliable. So, in order for the correlation coefficient of 0.70 to be reliable, at least 8 pairs of data must be taken into the analysis ( h =n-2=6) when calculating r (see Table 4 in the Appendix) and 7 pairs of data (h = n-2= 5) when calculating r s (Table 5 in the Appendix).

I would like to emphasize once again that the essence of these two coefficients is somewhat different. A negative coefficient r indicates that performance tends to be higher the shorter the reaction time, while the calculation of the coefficient r s required checking whether faster subjects always respond more accurately and slower ones less accurately.

Bravais-Pearson correlation coefficient (r) - This is a parametric indicator for the calculation of which the average and standard deviations of the results of two measurements are compared. In this case, they use the formula (it may look different for different authors):

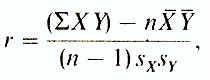
where Σ XY- the sum of the products of data from each pair;
n-number of pairs;
X - average for the given variable X;
Y - average for the given variable Y
S x - standard deviation for distribution X;
S y - standard deviation for distribution at

Spearman's rank correlation coefficient ( r s ) - this is a non-parametric indicator, with the help of which they try to identify the relationship between the ranks of corresponding quantities in two series of measurements.

This coefficient is easier to calculate, but the results are less accurate than using r. This is due to the fact that when calculating the Spearman coefficient, the order of the data is used, and not their quantitative characteristics and intervals between classes.

The fact is that when using the Spearman rank correlation coefficient (r s), they only check whether the ranking of the data for any sample will be the same as in a number of other data for this sample, pairwise related to the first ones (for example, whether they will be the same " ranked" students when they take both psychology and mathematics, or even with two different psychology teachers?). If the coefficient is close to +1, then this means that both series are practically identical, and if this coefficient is close to -1, we can talk about a complete inverse relationship.

Coefficient r s calculated by the formula

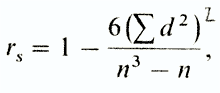
Where d- the difference between the ranks of conjugate values ​​of features (regardless of its sign), and - the number of pairs.

Typically, this nonparametric test is used in cases where it is necessary to draw some conclusions not so much about intervals between the data, how much about them ranks, and also when the distribution curves are too skewed to allow the use of parametric criteria such as the coefficient r (in these cases it may be necessary to convert quantitative data into ordinal data).

Summary

So, we have looked at various parametric and non-parametric statistical methods used in psychology. Our review was very superficial, and its main task was to make the reader understand that statistics are not as scary as they seem, and require mostly common sense. We remind you that the “experience” data we have dealt with here is fictitious and cannot serve as a basis for any conclusions. However, such an experiment would really be worth conducting. Since a purely classical technique was chosen for this experiment, the same statistical analysis could be used in many different experiments. In any case, it seems to us that we have outlined some main directions that may be useful to those who do not know where to start with a statistical analysis of the results obtained.

Literature

1. Godefroy J. What is psychology. - M., 1992.
2. Chatillon G., 1977. Statistique en Sciences humaines, Trois-Rivieres, Ed. SMG.
3. Gilbert N.. 1978. Statistiques, Montreal, Ed. HRW.
4. Moroney M. J., 1970. Comprendre la statistique, Verviers, Gerard et Cie.
5. Siegel S., 1956. Non-parametric Statistic, New York, MacGraw-Hill Book Co.

Tables app

Notes 1) For large samples or significance levels less than 0.05, you should refer to the tables in statistics textbooks.

2) Tables of values ​​for other non-parametric criteria can be found in special manuals (see bibliography).

Table 1. Criterion values t Student's test
h	0,05
1	6,31
2	2,92
3	2,35
4	2,13
5	2,02
6	1,94
7	1,90
8	1,86
9	1,83
10	1,81
11	1,80
12	1,78
13	1,77
14	1,76
15	1,75
16	1,75
17	1,74
18	1,73
19	1,73
20	1,73
21	1,72
22	1,72
23	1,71
24	1,71
25	1,71
26	1,71
27	1,70
28	1,70
29	1,70
30	1,70
40	1,68
¥	1,65

Table 2. Values ​​of the χ 2 criterion
h	0,05
1	3,84
2	5,99
3	7,81
4	9,49
5	11,1
6	12,6
7	14,1
8	15,5
9	16,9
10	18,3
Table 3. Significant Z values
R	Z
0,05	1,64
0,01	2,33

Table 4. Reliable (critical) r values
h =(N-2)		p= 0,05 (5%)
3		0,88
4		0,81
5		0,75
6		0,71
7		0,67
8		0,63
9		0,60
10		0,58
11		0.55
12		0,53
13		0,51
14		0,50
15		0,48
16		0,47
17		0,46
18		0,44
19		0,43
20		0,42

Table 5. Reliable (critical) values ​​of r s
h =(N-2)	p = 0,05
2	1,000
3	0,900
4	0,829
5	0,714
6	0,643
7	0,600
8	0,564
10	0,506
12	0,456
14	0,425
16	0,399
18	0,377
20	0,359
22	0,343
24	0,329
26	0,317
28	0,306

COURSE WORK

Topic: Correlation analysis

Introduction

1. Correlation analysis

1.1 The concept of correlation

1.2 General classification of correlations

1.3 Correlation fields and the purpose of their construction

1.4 Stages of correlation analysis

1.5 Correlation coefficients

1.6 Normalized Bravais-Pearson correlation coefficient

1.7 Spearman's rank correlation coefficient

1.8 Basic properties of correlation coefficients

1.9 Checking the significance of correlation coefficients

1.10 Critical values ​​of the pair correlation coefficient

2. Planning a multifactorial experiment

2.1 Condition of the problem

2.2 Determination of the center of the plan (basic level) and the level of factor variation

2.3 Construction of the planning matrix

2.4 Checking the homogeneity of dispersion and equivalence of measurement in different series

2.5 Regression equation coefficients

2.6 Reproducibility variance

2.7 Checking the significance of regression equation coefficients

2.8 Checking the adequacy of the regression equation

Conclusion

Bibliography

INTRODUCTION

Experimental planning is a mathematical and statistical discipline that studies methods for the rational organization of experimental research - from the optimal choice of factors under study and the determination of the actual experimental plan in accordance with its purpose to methods for analyzing the results. Experimental planning began with the works of the English statistician R. Fisher (1935), who emphasized that rational experimental planning provides no less significant gains in the accuracy of estimates than optimal processing of measurement results. In the 60s of the 20th century, the modern theory of experimental planning emerged. Her methods are closely related to function approximation theory and mathematical programming. Optimal plans were constructed and their properties were studied for a wide class of models.

Experimental planning is the choice of an experimental plan that meets specified requirements, a set of actions aimed at developing an experimentation strategy (from obtaining a priori information to obtaining a workable mathematical model or determining optimal conditions). This is purposeful control of an experiment, implemented under conditions of incomplete knowledge of the mechanism of the phenomenon being studied.

In the process of measurements, subsequent data processing, as well as formalization of the results in the form of a mathematical model, errors arise and some of the information contained in the original data is lost. The use of experimental planning methods makes it possible to determine the error of the mathematical model and judge its adequacy. If the accuracy of the model turns out to be insufficient, then the use of experimental planning methods makes it possible to modernize the mathematical model with additional experiments without losing previous information and with minimal costs.

The purpose of planning an experiment is to find such conditions and rules for conducting experiments under which it is possible to obtain reliable and reliable information about an object with the least amount of labor, as well as to present this information in a compact and convenient form with a quantitative assessment of accuracy.

Among the main planning methods used at different stages of the study are:

Planning a screening experiment, the main meaning of which is the selection from the entire set of factors of a group of significant factors that are subject to further detailed study;

Experimental design for ANOVA, i.e. drawing up plans for objects with qualitative factors;

Planning a regression experiment that allows you to obtain regression models (polynomial and others);

Planning an extreme experiment in which the main task is experimental optimization of the research object;

Planning when studying dynamic processes, etc.

The purpose of studying the discipline is to prepare students for production and technical activities in their specialty using methods of planning theory and modern information technologies.

Objectives of the discipline: study of modern methods of planning, organizing and optimizing scientific and industrial experiments, conducting experiments and processing the results obtained.

1. CORRELATION ANALYSIS

1.1 The concept of correlation

A researcher is often interested in how two or more variables are related to each other in one or more samples being studied. For example, can height affect a person's weight, or can blood pressure affect product quality?

This kind of dependence between variables is called correlation, or correlation. A correlation is a consistent change in two characteristics, reflecting the fact that the variability of one characteristic is in accordance with the variability of the other.

It is known, for example, that on average there is a positive relationship between the height of people and their weight, and such that the greater the height, the greater the person’s weight. However, there are exceptions to this rule, when relatively short people are overweight, and, conversely, asthenic people with high stature have low weight. The reason for such exceptions is that each biological, physiological or psychological sign is determined by the influence of many factors: environmental, genetic, social, environmental, etc.

Correlation connections are probabilistic changes that can only be studied on representative samples using the methods of mathematical statistics. Both terms - correlation link and correlation dependence - are often used interchangeably. Dependency implies influence, connection - any coordinated changes that can be explained by hundreds of reasons. Correlation connections cannot be considered as evidence of a cause-and-effect relationship; they only indicate that changes in one characteristic are usually accompanied by certain changes in another.

Correlation dependence - These are changes that introduce the values ​​of one characteristic into the probability of the occurrence of different values ​​of another characteristic.

The task of correlation analysis comes down to establishing the direction (positive or negative) and form (linear, nonlinear) of the relationship between varying characteristics, measuring its closeness, and, finally, checking the level of significance of the obtained correlation coefficients.

Correlation connections vary in form, direction and degree (strength) .

The form of the correlation relationship can be linear or curvilinear. For example, the relationship between the number of training sessions on the simulator and the number of correctly solved problems in the control session may be straightforward. For example, the relationship between the level of motivation and the effectiveness of a task may be curvilinear (Figure 1). As motivation increases, the effectiveness of completing a task first increases, then the optimal level of motivation is achieved, which corresponds to the maximum effectiveness of completing the task; A further increase in motivation is accompanied by a decrease in efficiency.

Figure 1 - Relationship between the effectiveness of problem solving and the strength of motivational tendencies

In direction, the correlation relationship can be positive (“direct”) and negative (“inverse”). With a positive linear correlation, higher values ​​of one characteristic correspond to higher values ​​of another, and lower values ​​of one characteristic correspond to low values ​​of another (Figure 2). With a negative correlation, the relationships are inverse (Figure 3). With a positive correlation, the correlation coefficient has a positive sign, with a negative correlation, it has a negative sign.

Figure 2 – Direct correlation

Figure 3 – Inverse correlation

Figure 4 – No correlation

The degree, strength or closeness of the correlation is determined by the value of the correlation coefficient. The strength of the connection does not depend on its direction and is determined by the absolute value of the correlation coefficient.

1.2 General classification of correlations

Depending on the correlation coefficient, the following correlations are distinguished:

Strong, or close with a correlation coefficient r>0.70;

Average (at 0.50

Moderate (at 0.30

Weak (at 0.20

Very weak (at r<0,19).

1.3 Correlation fields and the purpose of their construction

Correlation is studied on the basis of experimental data, which are the measured values ​​(x i, y i) of two characteristics. If there is little experimental data, then the two-dimensional empirical distribution is represented as a double series of values ​​x i and y i. At the same time, the correlation dependence between characteristics can be described in different ways. The correspondence between an argument and a function can be given by a table, formula, graph, etc.

Correlation analysis, like other statistical methods, is based on the use of probabilistic models that describe the behavior of the characteristics under study in a certain general population from which the experimental values ​​xi and y i are obtained. When studying the correlation between quantitative characteristics, the values ​​of which can be accurately measured in units of metric scales (meters, seconds, kilograms, etc.), a two-dimensional normally distributed population model is very often adopted. Such a model displays the relationship between the variables x i and y i graphically in the form of a geometric location of points in a system of rectangular coordinates. This graphical relationship is also called a scatterplot or correlation field.
This model of a two-dimensional normal distribution (correlation field) allows us to give a clear graphical interpretation of the correlation coefficient, because the distribution in total depends on five parameters: μ x, μ y – average values ​​(mathematical expectations); σ x ,σ y – standard deviations of random variables X and Y and p – correlation coefficient, which is a measure of the relationship between random variables X and Y.
If p = 0, then the values ​​x i , y i obtained from a two-dimensional normal population are located on the graph in coordinates x, y within the area limited by the circle (Figure 5, a). In this case, there is no correlation between the random variables X and Y and they are called uncorrelated. For a two-dimensional normal distribution, uncorrelatedness simultaneously means independence of random variables X and Y.

7.3.1. Coefficients of correlation and determination. Can be quantified closeness of communication between factors and its focus(direct or inverse), calculating:

1) if it is necessary to determine a linear relationship between two factors, - pair coefficient correlations: in 7.3.2 and 7.3.3 the operations of calculating the paired linear correlation coefficient according to Bravais–Pearson ( r) and paired Spearman rank correlation coefficient ( r);

2) if we want to determine the relationship between two factors, but this relationship is clearly nonlinear, then correlation relation ;

3) if we want to determine the relationship between one factor and a certain set of other factors, then (or, which is the same thing, “multiple correlation coefficient”);

4) if we want to identify in isolation the connection of one factor only with a specific other, included in the group of factors influencing the first, for which we have to consider the influence of all other factors unchanged - then partial correlation coefficient .

Any correlation coefficient (r, r) cannot exceed 1 in absolute value, that is –1< r (r) < 1). Если получено значение 1, то это значит, что рассматриваемая зависимость не статистическая, а функциональная, если 0 - корреляции нет вообще.

The sign of the correlation coefficient determines the direction of the relationship: the “+” sign (or no sign) means that the relationship straight (positive), the “–” sign means that the connection reverse (negative). The sign has nothing to do with the closeness of the connection

The correlation coefficient characterizes the statistical relationship. But often it is necessary to determine another type of dependence, namely: what is the contribution of a certain factor to the formation of another factor associated with it. This kind of dependence is, with some degree of convention, characterized coefficient of determination (D ), determined by the formula D = r 2 ´100% (where r is the Bravais–Pearson correlation coefficient, see 7.3.2). If measurements were carried out in order scale (rank scale), then with some damage to reliability, instead of the value r, you can substitute the value r (Spearman correlation coefficient, see 7.3.3) into the formula.

For example, if we obtained, as a characteristic of the dependence of factor B on factor A, the correlation coefficient r = 0.8 or r = –0.8, then D = 0.8 2 ´100% = 64%, that is, about 2 ½ 3. Consequently, the contribution of factor A and its changes to the formation of factor B is approximately 2 ½ 3 from the total contribution of all factors in general.

7.3.2. Bravais-Pearson correlation coefficient. The procedure for calculating the Bravais–Pearson correlation coefficient ( r ) can only be used in cases where the relationship is considered on the basis of samples having a normal frequency distribution ( normal distribution ) and obtained by measurements on interval or ratio scales. The calculation formula for this correlation coefficient is:

å ( x i – )( y i – )

r = .

n×s x ×s y

What does the correlation coefficient show? Firstly, the sign of the correlation coefficient shows the direction of the relationship, namely: the “–” sign indicates that the relationship reverse, or negative(there is a tendency: with a decrease in the values ​​of one factor, the corresponding values ​​of another factor increase, and with an increase, they decrease), and the absence of a sign or the “+” sign indicates straight, or positive connections (there is a tendency: with an increase in the values ​​of one factor, the values ​​of another increase, and with a decrease, they decrease). Secondly, the absolute (sign-independent) value of the correlation coefficient indicates the closeness (strength) of the connection. It is generally accepted (rather arbitrarily): for values ​​of r< 0,3 корреляция very weak, often it is simply not taken into account, at 0.3 £ r< 5 корреляция weak, at 0.5 £ r< 0,7) - average, at 0.7 £ r £ 0.9) - strong and finally, for r > 0.9 - very strong. In our case (r » 0.83) the relationship is inverse (negative) and strong.

Let us remind you: the values ​​of the correlation coefficient can be in the range from –1 to +1. If the value of r goes beyond these limits, it indicates that in the calculations a mistake was made . If r= 1, this means that the connection is not statistical, but functional - which practically never happens in sports, biology, or medicine. Although, with a small number of measurements, a random selection of values ​​that gives a picture of the functional connection is possible, such a case is less likely, the larger the volume of compared samples (n), that is, the number of pairs of compared measurements.

The calculation table (Table 7.1) is constructed according to the formula.

Table 7.1.

Calculation table for Bravais–Pearson calculations

x i	y i	(x i – )	(x i – ) 2	(y i – )	(y i – ) 2	(x i – )( y i – )
13,2	4,75	0,2	0,04	–0,35	0,1225	– 0,07
13,5	4,7	0,5	0,25	– 0,40	0,1600	– 0,20
12,7	5,10	– 0,3	0,09	0,00	0,0000	0,00
12,5	5,40	– 0,5	0,25	0,30	0,0900	– 0,15
13,0	5,10	0,0	0,00	0,00	0.0000	0,00
13,2	5,00	0,1	0,01	– 0,10	0,0100	– 0,02
13,1	5,00	0,1	0,01	– 0,10	0,0100	– 0,01
13,4	4,65	0,4	0,16	– 0,45	0,2025	– 0,18
12,4	5,60	– 0,6	0,36	0,50	0,2500	– 0,30
12,3	5,50	– 0,7	0,49	0,40	0,1600	– 0,28
12,7	5,20	–0,3	0,09	0,10	0,0100	– 0,03
åx i =137 =13.00	åy i =56.1 =5.1		å( x i – ) 2 = =1.78		å( y i – ) 2 = = 1.015	å( x i – )( y i – )= = –1.24

Because the s x = ï ï = ï ï» 0.42, a

s y = ï ï» 0,32, r" –1,24ï (11´0.42´0.32) » –1,24ï 1,48 » –0,83 .

In other words, you need to know very firmly that the correlation coefficient can not exceed 1.0 in absolute value. This often allows you to avoid gross mistakes, or more precisely, to find and correct errors made during calculations.

7.3.3. Spearman correlation coefficient. As already mentioned, the Bravais–Pearson correlation coefficient (r) can be used only in cases where the analyzed factors are close to normal in frequency distribution and the variant values ​​are obtained by measurements necessarily on a ratio scale or on an interval scale, which happens if they are expressed physical units. In other cases, the Spearman correlation coefficient is found ( r). However, this coefficient Can apply in cases where it is permitted (and desirable ! ) apply the Bravais-Pearson correlation coefficient. But it should be borne in mind that the procedure for determining the coefficient according to Bravais-Pearson has higher power (“resolving ability"), That's why r more informative than r. Even with great n deviation r may be on the order of ±10%.

Table 7.2 Calculation formula for coefficient

x i y i R x R y |d R | d R 2 Spearman correlation

13,2 4,75 8,5 3,0 5,5 30,25 r= 1 – . Vos

13.5 4.70 11.0 2.0 9.0 81.00 we use our example

12.7 5.10 4.5 6.5 2.0 4.00 for calculation r, but we'll build

12.5 5.40 3.0 9.0 6.0 36.00 another table (Table 7.2).

13.0 5.10 6.0 6.5 0.5 0.25 Let’s substitute the values:

13.2 5.00 8.5 4.5 4.0 16.00 r = 1– =

13,1 5,00 7,0 4,5 2,5 6,25 =1– 2538:1320 » 1–1,9 » – 0,9.

13.4 4.65 10.0 1.0 9.0 81.00 We see: r turned out to be a little

12.4 5.60 2.0 11.0 9.0 81.00 more than r, but this is different

12.3 5.50 1.0 10.0 9.0 81.00 which is not very large. After all, when

12.7 5.20 4.5 8.0 3.5 12.25 so small n values r And r

åd R 2 = 423 are very approximate, not very reliable, their actual value can vary widely, so the difference r And r at 0.1 is insignificant. Usuallyrconsidered as an analoguer , but only less accurate. Signs when r And r shows the direction of the connection.

7.3.4. Application and verification of the reliability of correlation coefficients. Determining the degree of correlation between factors is necessary to control the development of the factor we need: to do this, we have to influence other factors that significantly influence it, and we need to know the extent of their effectiveness. It is necessary to know about the relationship between factors in order to develop or select ready-made tests: the information content of a test is determined by the correlation of its results with the manifestations of the characteristic or property that interests us. Without knowledge of correlations, any form of selection is impossible.

It was noted above that in sports and in general pedagogical, medical and even economic and sociological practice, the determination of what contribution , which one factor contributes to the formation of another. This is due to the fact that, in addition to the factor-cause under consideration, target(the factor that interests us) act, giving each one one or another contribution to it, and others.

It is believed that the measure of the contribution of each factor-cause can be coefficient of determination D i = r 2 ´100%. So, for example, if r = 0.6, i.e. the relationship between factors A and B is average, then D = 0.6 2 ´100% = 36%. Knowing, therefore, that the contribution of factor A to the formation of factor B is approximately 1 ½ 3, you can, for example, devote approximately 1 to the targeted development of this factor ½ 3 training times. If the correlation coefficient is r = 0.4, then D = r 2 100% = 16%, or approximately 1 ½ 6 is more than two times less, and according to this logic, according to this logic, only 1 should be devoted to its development ½ 6th part of training time.

The values ​​of D i for various significant factors give an approximate idea of ​​​​the quantitative relationship of their influences on the target factor of interest to us, for the sake of improving which we, in fact, work on other factors (for example, a running long jumper works to increase the speed of his sprinting, so how it is the factor that makes the most significant contribution to the formation of results in jumping).

Recall that defining D maybe instead r put r, although, of course, the accuracy of the determination turns out to be lower.

Based selective correlation coefficient (calculated from sample data), one cannot draw a conclusion about the reliability of the fact that there is a connection between the factors under consideration in general. In order to make such a conclusion with varying degrees of validity, standard correlation significance criteria. Their use assumes a linear relationship between factors and normal distribution frequencies in each of them (meaning not a selective, but their general representation).

You can, for example, use Student's t-tests. His dis-

even formula: t p= –2 , where k is the sample correlation coefficient under study, a n- volume of compared samples. The resulting calculated value of the t-criterion (t p) is compared with the table at the significance level we have chosen and the number of degrees of freedom n = n – 2. To get rid of the calculation work, you can use a special table critical values ​​of sample correlation coefficients(see above), corresponding to the presence of a reliable connection between factors (taking into account n And a).

Table 7.3.

Boundary values ​​for the reliability of the sample correlation coefficient

The number of degrees of freedom when determining correlation coefficients is taken equal to 2 (i.e. n= 2) Indicated in the table. 7.3 values ​​have the lower limit of the confidence interval true correlation coefficient is 0, that is, with such values ​​it cannot be argued that correlation occurs at all. If the value of the sample correlation coefficient is higher than that indicated in the table, it can be assumed, at the appropriate level of significance, that the true correlation coefficient is not equal to zero.

But the answer to the question whether there is a real connection between the factors under consideration leaves room for another question: in what interval does the true meaning correlation coefficient, as it may actually be, for an infinitely large n? This interval for any particular value r And n comparable factors can be calculated, but it is more convenient to use a graph system ( nomogram), where each pair of curves constructed for some specified above them n, corresponds to the boundaries of the interval.

Rice. 7.4. Confidence limits of the sample correlation coefficient (a = 0.05). Each curve corresponds to the one indicated above it n.

Referring to the nomogram in Fig. 7.4, it is possible to determine the interval of values ​​of the true correlation coefficient for the calculated values ​​of the sample correlation coefficient at a = 0.05.

7.3.5. Correlation relationships. If pairwise correlation nonlinear, it is impossible to calculate the correlation coefficient, determine correlation relationships . Mandatory requirement: characteristics must be measured on a ratio scale or on an interval scale. You can calculate the correlation dependence of the factor X from factor Y and correlation dependence of the factor Y from factor X- they differ. For small volume n of the considered samples representing factors, to calculate correlation relationships, you can use the formulas:

correlation ratio h x½y= ;

correlation relation h y ½ x= .

Here and are the arithmetic means of samples X and Y, and - intraclass arithmetic averages. That is, the arithmetic mean of those values ​​in the sample of factor X with which identical values ​​are conjugate in the sample of factor Y (for example, if in factor X there are values ​​4, 6, and 5, with which in the sample of factor Y there are associated 3 options with the same value 9, then = (4+6+5) ½ 3 = 5). Accordingly, it is the arithmetic mean of those values ​​in the sample of factor Y, which are associated with the same values ​​in the sample of factor X. Let’s give an example and carry out the calculation:

X: 75 77 78 76 80 79 83 82 ; Y: 42 42 43 43 43 44 44 45 .

Table 7.4

Calculation table

x i	y i	x y	x i – x	(x i – x) 2	x i – x y	(x i–x y) 2
			–4		–1
			–2
			–3		–2
			–1
					–3
x=79	y=43			S=76		S=28

Therefore, h y ½ x= "0.63.

7.3.6. Partial and multiple correlation coefficients. To assess the dependence between 2 factors, when calculating correlation coefficients, we assume by default that no other factors have any effect on this dependence. In reality this is not the case. Thus, the relationship between weight and height is very significantly influenced by caloric intake, the amount of systematic physical activity, heredity, etc. When necessary when assessing the relationship between 2 factors take into account the significant impact other factors and at the same time, as it were, isolate yourself from them, considering them unchanged, calculate private (otherwise - partial ) correlation coefficients.

Example: we need to evaluate paired dependencies between 3 significantly active factors X, Y and Z. Let us denote r XY (Z) partial correlation coefficient between factors X and Y (in this case, the value of factor Z is considered unchanged), r ZX (Y) - partial correlation coefficient between factors Z and X (with a constant value of factor Y), r YZ (X) - partial correlation coefficient between factors Y and Z (with a constant value of factor X). Using the calculated simple paired (Bravais-Pearson) correlation coefficients r XY, r XZ and r YZ, m

You can calculate partial correlation coefficients using the formulas:

r XY – r XZ´ r YZ r XZ – r XY´ r ZY r ZY –r ZX ´ r YZ

r XY(Z) = ; r XZ(Y) = ; r ZY(X) =

Ö(1– r 2 XZ)(1– r 2 YZ) Ö(1– r 2 XY)(1– r 2 ZY) Ö(1– r 2 ZX)(1– r 2 YX)

And partial correlation coefficients can take values ​​from –1 to +1. By squaring them, we obtain the corresponding quotients coefficients of determination , also called private measures of certainty(multiply by 100 and express it as %%). Partial correlation coefficients differ more or less from simple (full) pair coefficients, which depends on the strength of influence of the 3rd factor (as if unchanged) on them. The null hypothesis (H 0), that is, the hypothesis about the absence of a connection (dependence) between factors X and Y, is tested (with a total number of signs k) by calculating the t-test using the formula: t P = r XY (Z) ´ ( n–k) 1 ½ 2 ´ (1– r 2 XY (Z)) –1 ½ 2 .

If t R< t a n , the hypothesis is accepted (we assume that there is no dependence), but if t P³ t a n - the hypothesis is refuted, that is, it is believed that the dependence really takes place. t a n is taken from the table t-Student's test, and k- the number of factors taken into account (in our example 3), the number of degrees of freedom n= n – 3. Other partial correlation coefficients are checked similarly (in the formula instead r XY (Z) is substituted accordingly r XZ(Y) or r ZY(X)).

Table 7.5

Initial data

Ö (1 – 0.71 2)(1 – 0.71 2) Ö (1 – 0.5)(1 – 0.5)

To assess the dependence of factor X on the combined action of several factors (here factors Y and Z), calculate the values ​​of simple pair correlation coefficients and, using them, calculate multiple correlation coefficient r X (YZ) :

Ö r 2XY+ r 2 XZ – 2 r XY´ r XZ´ r YZ

r X(YZ) = .

Ö 1 – r 2 YZ

7.2.7. Association coefficient. It is often necessary to quantify the relationship between quality signs, i.e. such characteristics that cannot be represented (characterized) quantitatively, which immeasurable. For example, the task is to find out whether there is a relationship between the sports specialization of those involved and such personal properties as introversion (the personality’s focus on the phenomena of their own subjective world) and extroversion (the personality’s focus on the world of external objects). We present the symbols in the table. 7.6.

Table 7.6.

X (years)	Y (times)	Z (times)		X (years)	Y (times)	Z (times)

Sign 1 Sign 2	Introversion	Extroversion
Sport games	A	b
Gymnastics	With	d

Obviously, the numbers at our disposal here can only be distribution frequencies. In this case, calculate association coefficient (other name " contingency coefficient "). Let's consider the simplest case: a relationship between two pairs of features, and the calculated contingency coefficient is called tetrachoric (see table).

Table 7.7.

a =20	b = 15	a + b = 35
s =15	d=5	c + d = 20
a + c = 35	b + d = 20	n = 55

We make calculations using the formula:

ad – bc 100 – 225 –123

The calculation of association coefficients (conjugation coefficients) with a larger number of characteristics involves calculations using a similar matrix of the appropriate order.

The correlation coefficient (or linear correlation coefficient) is denoted as "r" (in rare cases as "ρ") and characterizes the linear correlation (that is, the relationship that is given by some value and direction) of two or more variables. The coefficient value lies between -1 and +1, that is, the correlation can be both positive and negative. If the correlation coefficient is -1, there is a perfect negative correlation; if the correlation coefficient is +1, there is a perfect positive correlation. In other cases, there is a positive correlation, a negative correlation, or no correlation between two variables. The correlation coefficient can be calculated manually, using free online calculators, or using a good graphing calculator.

Steps

Calculating the correlation coefficient manually

Collect data. Before you start calculating the correlation coefficient, study the given pair of numbers. It is better to write them down in a table that can be placed vertically or horizontally. Label each row or column as "x" and "y".

• For example, four pairs of values ​​(numbers) of the variables “x” and “y” are given. You can create the following table:
  • x || y
  • 1 || 1
  • 2 || 3
  • 4 || 5
  • 5 || 7

1. Calculate the arithmetic mean of "x". To do this, add up all the “x” values, and then divide the resulting result by the number of values.

   Find the arithmetic mean "y". To do this, follow similar steps, that is, add up all the values ​​of “y”, and then divide the sum by the number of values.

   Calculate the standard deviation of "x". After calculating the means of x and y, find the standard deviations of these variables. The standard deviation is calculated using the following formula:

   Calculate the standard deviation of "y". Follow the steps described in the previous step. Use the same formula, but substitute the “y” values ​​into it.

   Write down the basic formula for calculating the correlation coefficient. This formula includes the means, standard deviations, and number (n) pairs of numbers for both variables. The correlation coefficient is denoted as "r" (in rare cases as "ρ"). This article uses a formula to calculate the Pearson correlation coefficient.

   You have calculated the means and standard deviations of both variables, so you can use the formula to calculate the correlation coefficient. Recall that “n” is the number of pairs of values ​​for both variables. The values ​​of other quantities were calculated earlier.

   • In our example, the calculations will be written like this:
   • ρ = (1 n − 1) Σ (x − μ x σ x) ∗ (y − μ y σ y) (\displaystyle \rho =\left((\frac (1)(n-1))\right) \Sigma \left((\frac (x-\mu _(x))(\sigma _(x)))\right)*\left((\frac (y-\mu _(y))(\sigma _(y)))\right))
   • ρ = (1 3) ∗ (\displaystyle \rho =\left((\frac (1)(3))\right)*)[ (1 − 3 1 , 83) ∗ (1 − 4 2 , 58) + (2 − 3 1 , 83) ∗ (3 − 4 2 , 58) (\displaystyle \left((\frac (1-3)( 1.83))\right)*\left((\frac (1-4)(2.58))\right)+\left((\frac (2-3)(1.83))\right) *\left((\frac (3-4)(2.58))\right))
     + (4 − 3 1 , 83) ∗ (5 − 4 2 , 58) + (5 − 3 1 , 83) ∗ (7 − 4 2 , 58) (\displaystyle +\left((\frac (4-3 )(1.83))\right)*\left((\frac (5-4)(2.58))\right)+\left((\frac (5-3)(1.83))\ right)*\left((\frac (7-4)(2.58))\right))]
   • ρ = (1 3) ∗ (6 + 1 + 1 + 6 4 , 721) (\displaystyle \rho =\left((\frac (1)(3))\right)*\left((\frac (6 +1+1+6)(4,721))\right))
   • ρ = (1 3) ∗ 2 , 965 (\displaystyle \rho =\left((\frac (1)(3))\right)*2.965)
   • ρ = (2 , 965 3) (\displaystyle \rho =\left((\frac (2.965)(3))\right))
   • ρ = 0.988 (\displaystyle \rho =0.988)

2. Analyze the result. In our example, the correlation coefficient is 0.988. This value in some way characterizes this set of pairs of numbers. Pay attention to the sign and magnitude of the value.

   • Since the value of the correlation coefficient is positive, there is a positive correlation between the variables “x” and “y”. That is, as the value of “x” increases, the value of “y” also increases.
   • Since the value of the correlation coefficient is very close to +1, the values ​​of the variables “x” and “y” are highly interrelated. If you plot points on the coordinate plane, they will be located close to a certain straight line.

   Using online calculators to calculate the correlation coefficient

   1. Find a calculator on the Internet to calculate the correlation coefficient. This coefficient is quite often calculated in statistics. If there are many pairs of numbers, it is almost impossible to calculate the correlation coefficient manually. Therefore, there are online calculators for calculating the correlation coefficient. In a search engine, enter “correlation coefficient calculator” (without quotes).

      Enter data. Please review the instructions on the website to ensure that you enter the data (number pairs) correctly. It is extremely important to enter the appropriate pairs of numbers; otherwise you will get an incorrect result. Remember that different websites have different data entry formats.

      • For example, on the website http://ncalculators.com/statistics/correlation-coefficient-calculator.htm the values ​​of the variables “x” and “y” are entered in two horizontal lines. Values ​​are separated by commas. That is, in our example, the “x” values ​​are entered like this: 1,2,4,5, and the “y” values ​​like this: 1,3,5,7.
      • On another site, http://www.alcula.com/calculators/statistics/correlation-coefficient/, data is entered vertically; in this case, do not confuse the corresponding pairs of numbers.

   2. Calculate the correlation coefficient. After entering the data, simply click on the “Calculate”, “Calculate” or similar button to get the result.

   Using a graphing calculator

   1. Enter data. Take a graphing calculator, go into statistical mode and select the Edit command.

      • Different calculators require different keystrokes to be pressed. This article discusses the Texas Instruments TI-86 calculator.
      • To switch to statistical calculation mode, press – Stat (above the “+” key). Then press F2 – Edit.

   2. Delete previous saved data. Most calculators store the statistics you enter until you clear them. To avoid confusing old data with new data, first delete any stored information.

      • Use the arrow keys to move the cursor and highlight the "xStat" heading. Then press Clear and Enter to remove all values ​​entered in the xStat column.
      • Use the arrow keys to highlight the "yStat" heading. Then press Clear and Enter to clear all values ​​entered in the yStat column.

   3. Enter the initial data. Use the arrow keys to move the cursor to the first cell under the "xStat" heading. Enter the first value and press Enter. “xStat (1) = __” will be displayed at the bottom of the screen, where the entered value will appear instead of a space. After you press Enter, the entered value will appear in the table and the cursor will move to the next line; this will display “xStat (2) = __” at the bottom of the screen.

      • Enter all values ​​for the variable "x".
      • After entering all the values ​​for the x variable, use the arrow keys to move to the yStat column and enter the values ​​for the y variable.
      • Once all pairs of numbers have been entered, press Exit to clear the screen and exit the statistical calculation mode.

Correlation coefficient is a value that can vary from +1 to –1. In the case of a complete positive correlation, this coefficient is equal to plus 1 (they say that when the value of one variable increases, the value of another variable increases), and in the case of a completely negative correlation, it is minus 1 (indicating feedback, i.e., when the values ​​of one variable increase, the values ​​of the other decrease).

Ex.1:

Graph of the relationship between shyness and depression. As you can see, the points (subjects) are not located chaotically, but line up around one line, and, looking at this line, we can say that the higher a person’s shyness, the greater the depression, i.e. these phenomena are interconnected.

Ex2: Chart for Shyness and Sociability. We see that as shyness increases, sociability decreases. Their correlation coefficient is -0.43. Thus, a correlation coefficient greater than 0 to 1 indicates a directly proportional relationship (the more... the more...), and a coefficient from -1 to 0 indicates an inversely proportional relationship (the more... the less...)

If the correlation coefficient is 0, both variables are completely independent of each other.

Correlation- this is a relationship where the impact of individual factors appears only as a trend (on average) during mass observation of actual data. Examples of correlation dependencies can be the dependencies between the size of the bank’s assets and the amount of the bank’s profit, the growth of labor productivity and the length of service of employees.

Two systems are used to classify correlations according to their strength: general and specific.

General classification of correlations: 1) strong, or close with a correlation coefficient r>0.70; 2) average with 0.500.70, and not just a correlation of a high level of significance.

The following table shows the names of the correlation coefficients for various types of scales.

	Dichotomous scale (1/0)	Rank (ordinal) scale
Dichotomous scale (1/0)	Pearson's coefficient of association, Pearson's four-cell contingency coefficient.		Biserial correlation
Rank (ordinal) scale	Rank-biserial correlation.	Spearman or Kendall rank correlation coefficient.
Interval and absolute scale	Biserial correlation	The values ​​of the interval scale are converted into ranks and the rank coefficient is used	Pearson correlation coefficient (linear correlation coefficient)

At r=0 There is no linear correlation. In this case, the group means of the variables coincide with their overall means, and the regression lines are parallel to the coordinate axes.

Equality r=0 speaks only about the absence of a linear correlation dependence (uncorrelated variables), but not generally about the absence of a correlation, and even more so, a statistical dependence.

Sometimes a finding of no correlation is more important than the presence of a strong correlation. A zero correlation between two variables may indicate that there is no influence of one variable on the other, provided we trust the measurement results.

In SPSS: 11.3.2 Correlation coefficients

Until now, we have only clarified the fact of the existence of a statistical relationship between two characteristics. Next, we will try to find out what conclusions can be drawn about the strength or weakness of this dependence, as well as about its type and direction. Criteria for quantifying the relationship between variables are called correlation coefficients or measures of connectivity. Two variables are positively correlated if there is a direct, unidirectional relationship between them. In a unidirectional relationship, small values ​​of one variable correspond to small values ​​of another variable, and large values ​​correspond to large values. Two variables correlate negatively with each other if there is an inverse, multidirectional relationship between them. With a multidirectional relationship, small values ​​of one variable correspond to large values ​​of another variable and vice versa. The values ​​of correlation coefficients always lie in the range from -1 to +1.

The Spearman coefficient is used as a correlation coefficient between variables belonging to an ordinal scale, and the Pearson correlation coefficient (moment of products) is used for variables belonging to an interval scale. It should be taken into account that each dichotomous variable, that is, a variable belonging to a nominal scale and having two categories, can be considered as ordinal.

First, we will check if there is a correlation between the sex and psyche variables from the studium.sav file. At the same time, we will take into account that the dichotomous variable sex can be considered ordinal. Follow these steps:

· Select from the command menu Analyze Descriptive Statistics Crosstabs...

· Move the variable sex to the list of rows and the variable psyche to the list of columns.

· Click on the Statistics... button. In the Crosstabs: Statistics dialog, select the Correlations checkbox. Confirm your selection with the Continue button.

· In the Crosstabs dialog, disable the display of tables by checking the Supress tables checkbox. Click OK.

Spearman and Pearson correlation coefficients will be calculated and their significance tested:

/ SPSS 10

Task No. 10 Correlation analysis

Concept of correlation

Correlation or correlation coefficient is a statistical indicator probabilistic relationships between two variables measured on quantitative scales. Unlike a functional relationship, in which each value of one variable corresponds strictly defined the value of another variable, probabilistic connection characterized by the fact that each value of one variable corresponds multiple meanings another variable. An example of a probabilistic relationship is the relationship between people's height and weight. It is clear that people of different weights can have the same height and vice versa.

Correlation is a value ranging from -1 to + 1 and is denoted by the letter r. Moreover, if the value is closer to 1, then this means the presence of a strong connection, and if closer to 0, then it is weak. A correlation value of less than 0.2 is considered a weak correlation, and a value greater than 0.5 is considered a high correlation. If the correlation coefficient is negative, this means that there is feedback: the higher the value of one variable, the lower the value of the other.

Depending on the accepted values ​​of the coefficient r, various types of correlation can be distinguished:

Strict positive correlation determined by the value r=1. The term "strict" means that the value of one variable is uniquely determined by the values ​​of another variable, and the term " positive" - that as the values ​​of one variable increase, the values ​​of another variable also increase.

Strict correlation is a mathematical abstraction and practically never occurs in real research.

Positive correlation corresponds to values ​​0

No correlation determined by the value r=0. A zero correlation coefficient indicates that the values ​​of the variables are in no way related to each other.

No correlation H o : 0 r xy =0 formulated as a reflection null hypotheses in correlation analysis.

Negative correlation: -1

Strict negative correlation determined by the value r= -1. It, like a strict positive correlation, is an abstraction and does not find expression in practical research.

Table 1

Types of correlation and their definitions

The method for calculating the correlation coefficient depends on the type of scale on which the variable values ​​are measured.

Correlation coefficient rPearson is basic and can be used for variables with nominal and partially ordered interval scales, the distribution of values ​​​​on which corresponds to normal (product moment correlation). The Pearson correlation coefficient gives fairly accurate results in cases of abnormal distributions.

For distributions that are not normal, it is preferable to use Spearman and Kendall rank correlation coefficients. They are ranked because the program pre-ranks the correlated variables.

The SPSS program calculates Spearman's correlation as follows: first, the variables are converted to ranks, and then the Pearson's formula is applied to the ranks.

The basis of the correlation proposed by M. Kendall is the idea that the direction of the connection can be judged by comparing subjects in pairs. If for a pair of subjects the change in X coincides in direction with the change in Y, then this indicates a positive connection. If it does not match, then there is a negative connection. This coefficient is used primarily by psychologists working with small samples. Since sociologists work with large amounts of data, enumerating pairs and identifying the difference in relative frequencies and inversions of all pairs of subjects in the sample is difficult. The most common is the coefficient. Pearson.

Since the Pearson correlation coefficient r is basic and can be used (with some error depending on the type of scale and the level of abnormality in the distribution) for all variables measured on quantitative scales, we will consider examples of its use and compare the results obtained with the results of measurements using other correlation coefficients.

Formula for calculating the coefficient r- Pearson:

r xy = ∑ (Xi-Xavg)∙(Yi-Yavg) / (N-1)∙σ x ∙σ y ∙

Where: Xi, Yi - Values ​​of two variables;

Xavg, Yavg - average values ​​of two variables;

σ x, σ y – standard deviations,

N is the number of observations.

Pairwise correlations

For example, we would like to find out how the answers correlate between different types of traditional values ​​in students’ ideas about an ideal place to work (variables: a9.1, a9.3, a9.5, a9.7), and then about the correlation between liberal values ​​(a9 .2, a9.4, a9.6, a9.8) . These variables are measured on 5-item ordered scales.

We use the procedure: “Analysis”,  “Correlations”,  “Paired”. Default coefficient Pearson is set in the dialog box. We use the coefficient. Pearson

The tested variables are transferred to the selection window: a9.1, a9.3, a9.5, a9.7

By clicking OK we get the calculation:

Correlations

a9.1.t. How important is it to have enough time for family and personal life?	Pearson correlation
	Value(2 sides)
a9.3.t. How important is it not to be afraid of losing your job?	Pearson correlation
	Value(2 sides)
a9.5.t. How important is it to have a boss who will consult with you when making this or that decision?	Pearson correlation
	Value(2 sides)
a9.7.t. How important is it to work in a well-coordinated team and feel like part of it?	Pearson correlation
	Value(2 sides)

** Correlation is significant at the 0.01 level (2-sided).

Table of quantitative values ​​of the constructed correlation matrix

Partial correlations:

First, let's build a pairwise correlation between these two variables:

Correlations
s8. Feel close to those who live next to you, neighbors	Pearson correlation
	Value(2 sides)
s12. Feel close to their family	Pearson correlation
	Value(2 sides)
**. The correlation is significant at the 0.01 level (2-sided).

Then we use the procedure for constructing a partial correlation: “Analysis”,  “Correlations”,  “Partial”.

Let us assume that the value “It is important to independently determine and change the order of your work” in relation to the specified variables turns out to be the decisive factor under the influence of which the previously identified relationship will disappear or turn out to be insignificant.

Correlations
Excluded Variables			s8. Feel close to those who live next to you, neighbors	s12. Feel close to their family
p16. Feel close to people who have the same income as you	s8. Feel close to those who live next to you, neighbors	Correlation
		Significance (2-sided)
	s12. Feel close to their family	Correlation
		Significance (2-sided)

As can be seen from the table, under the influence of the control variable, the relationship decreased slightly: from 0.120 to 0.102. However, this slight decrease does not allow us to state that the previously identified relationship is a reflection of a false correlation, because it remains quite high and allows us to reject the null hypothesis with zero error.

Correlation coefficient

The most accurate way to determine the closeness and nature of the correlation is to find the correlation coefficient. The correlation coefficient is a number determined by the formula:

where r xy is the correlation coefficient;

x i - values ​​of the first characteristic;

y i are the values ​​of the second attribute;

Arithmetic mean of the values ​​of the first characteristic

Arithmetic mean of the values ​​of the second characteristic

To use formula (32), we will build a table that will provide the necessary consistency in preparing numbers to find the numerator and denominator of the correlation coefficient.

As can be seen from formula (32), the sequence of actions is as follows: we find the arithmetic averages of both characteristics x and y, we find the difference between the values ​​of the attribute and its average (x i - ) and y i - ), then we find their product (x i - ) ( y i - ) – the sum of the latter gives the numerator of the correlation coefficient. To find its denominator, the differences (x i - ) and (y i - ) must be squared, their sums must be found, and the square root of their product must be taken.

So for example 31, finding the correlation coefficient in accordance with formula (32) can be represented as follows (Table 50).

The resulting number of the correlation coefficient makes it possible to establish the presence, closeness and nature of the connection.

1. If the correlation coefficient is zero, there is no connection between the characteristics.

2. If the correlation coefficient is equal to one, the connection between the characteristics is so great that it turns into a functional one.

3. The absolute value of the correlation coefficient does not go beyond the interval from zero to one:

This makes it possible to focus on the closeness of the connection: the closer the coefficient is to zero, the weaker the connection, and the closer to unity, the closer the connection.

4. The “plus” sign of the correlation coefficient means direct correlation, the “minus” sign means inverse correlation.

Table 50

x i	y i	(x i - )	(у i - )	(x i - )(y i - )	(x i - )2	(у i - )2
14,00	12,10	-1,70	-2,30	+3,91	2,89	5,29
14,20	13,80	-1,50	-0,60	+0,90	2,25	0,36
14,90	14,20	-0,80	-0,20	+0,16	0,64	0,04
15,40	13,00	-0,30	-1,40	+0,42	0,09	1,96
16,00	14,60	+0,30	+0,20	+0,06	0,09	0,04
17,20	15,90	+1,50	+2,25	2,25
18,10	17,40	+2,40	+2,00	+4,80	5,76	4,00
109,80	101,00		12,50	13,97	13,94

Thus, the correlation coefficient calculated in example 31 is r xy = +0.9. allows us to draw the following conclusions: there is a correlation between the magnitude of muscle strength of the right and left hands in the studied schoolchildren (coefficient r xy =+0.9 is different from zero), the relationship is very close (coefficient r xy =+0.9 is close to one), the correlation is direct (coefficient r xy = +0.9 is positive), i.e., with an increase in the muscle strength of one of the hands, the strength of the other hand increases.

When calculating the correlation coefficient and using its properties, it should be taken into account that the conclusions give correct results when the characteristics are normally distributed and when the relationship between a large number of values ​​of both characteristics is considered.

In the considered example 31, only 7 values ​​of both characteristics were analyzed, which, of course, is not enough for such studies. We remind you here once again that the examples in this book in general and in this chapter in particular are in the nature of illustrating methods, and not a detailed presentation of any scientific experiments. As a result, a small number of feature values ​​were considered, measurements were rounded - all this was done so that cumbersome calculations did not obscure the idea of ​​the method.

Particular attention should be paid to the essence of the relationship under consideration. The correlation coefficient cannot lead to correct research results if the relationship between characteristics is analyzed formally. Let us return once again to example 31. Both considered signs were the values ​​of muscle strength of the right and left hands. Let's imagine that by sign x i in example 31 (14.0; 14.2; 14.9... ...18.1) we mean the length of accidentally caught fish in centimeters, and by sign y i (12.1 ; 13.8; 14.2... ...17.4) - the weight of the instruments in the laboratory in kilograms. Having formally used the calculation apparatus to find the correlation coefficient and in this case also obtained r xy =+0>9, we had to conclude that there is a close direct relationship between the length of the fish and the weight of the instruments. The meaninglessness of such a conclusion is obvious.

To avoid a formal approach to using the correlation coefficient, one should use any other method - mathematical, logical, experimental, theoretical - to identify the possibility of the existence of a correlation between characteristics, that is, to discover the organic unity of characteristics. Only after this can one begin to use correlation analysis and establish the magnitude and nature of the relationship.

In mathematical statistics there is also the concept multiple correlation- relationships between three or more characteristics. In these cases, a multiple correlation coefficient is used, consisting of the paired correlation coefficients described above.

For example, the correlation coefficient of three characteristics - x i, y i, z i - is:

where R xyz is the multiple correlation coefficient, expressing how feature x i depends on features y i and z i;

r xy - correlation coefficient between characteristics x i and y i;

r xz - correlation coefficient between characteristics Xi and Zi;

r yz - correlation coefficient between features y i , z i

Correlation analysis is:

Correlation analysis

Correlation- statistical relationship between two or more random variables (or variables that can be considered as such with some acceptable degree of accuracy). Moreover, changes in one or more of these quantities lead to a systematic change in another or other quantities. A mathematical measure of the correlation between two random variables is the correlation coefficient.

The correlation can be positive and negative (it is also possible that there is no statistical relationship - for example, for independent random variables). Negative correlation - correlation, in which an increase in one variable is associated with a decrease in another variable, and the correlation coefficient is negative. Positive correlation - correlation, in which an increase in one variable is associated with an increase in another variable, and the correlation coefficient is positive.

Autocorrelation - statistical relationship between random variables from the same series, but taken with a shift, for example, for a random process - with a time shift.

The method of processing statistical data, which consists in studying the coefficients (correlation) between variables, is called correlation analysis.

Correlation coefficient

Correlation coefficient or pair correlation coefficient in probability theory and statistics, it is an indicator of the nature of the change in two random variables. The correlation coefficient is denoted by the Latin letter R and can take values ​​between -1 and +1. If the absolute value is closer to 1, then this means the presence of a strong connection (if the correlation coefficient is equal to one, we speak of a functional connection), and if it is closer to 0, then it is weak.

Pearson correlation coefficient

For metric quantities, the Pearson correlation coefficient is used, the exact formula of which was introduced by Francis Galton:

Let X,Y- two random variables defined on the same probability space. Then their correlation coefficient is given by the formula:

,

where cov denotes covariance and D is variance, or equivalently,

,

where the symbol denotes the mathematical expectation.

To graphically represent such a relationship, you can use a rectangular coordinate system with axes that correspond to both variables. Each pair of values ​​is marked with a specific symbol. This graph is called a “scatterplot.”

The method for calculating the correlation coefficient depends on the type of scale to which the variables belong. Thus, to measure variables with interval and quantitative scales, it is necessary to use the Pearson correlation coefficient (product moment correlation). If at least one of the two variables is on an ordinal scale or is not normally distributed, Spearman's rank correlation or Kendal's τ (tau) must be used. In the case where one of the two variables is dichotomous, a point-biserial correlation is used, and if both variables are dichotomous: a four-field correlation. Calculating the correlation coefficient between two non-dichotomous variables makes sense only when the relationship between them is linear (unidirectional).

Kendell correlation coefficient

Used to measure mutual disorder.

Spearman correlation coefficient

Properties of the correlation coefficient

• Cauchy-Bunyakovsky inequality:

if we take covariance as the scalar product of two random variables, then the norm of the random variable will be equal to , and the consequence of the Cauchy-Bunyakovsky inequality will be: . , Where . Moreover, in this case the signs and k match up: .

Correlation analysis

Correlation analysis- method of processing statistical data, which consists in studying coefficients ( correlations) between variables. In this case, correlation coefficients between one pair or many pairs of characteristics are compared to establish statistical relationships between them.

Target correlation analysis- provide some information about one variable using another variable. In cases where it is possible to achieve a goal, the variables are said to be correlate. In its most general form, accepting the hypothesis of a correlation means that a change in the value of variable A will occur simultaneously with a proportional change in the value of B: if both variables increase, then the correlation is positive, if one variable increases and the other decreases, correlation is negative.

Correlation reflects only the linear dependence of values, but does not reflect their functional connectivity. For example, if you calculate the correlation coefficient between the quantities A = sin(x) And B = cos(x), then it will be close to zero, i.e. there is no dependence between the quantities. Meanwhile, quantities A and B are obviously related functionally according to the law sin 2(x) + cos 2(x) = 1.

Limitations of Correlation Analysis

Graphs of distributions of pairs (x,y) with the corresponding correlation coefficients x and y for each of them. Note that the correlation coefficient reflects a linear relationship (top line), but does not describe a relationship curve (middle line), and is not at all suitable for describing complex, nonlinear relationships (bottom line).

1. Application is possible if there are a sufficient number of cases for study: for a particular type, the correlation coefficient ranges from 25 to 100 pairs of observations.
2. The second limitation follows from the correlation analysis hypothesis, which includes linear dependence of variables. In many cases, when it is reliably known that a relationship exists, correlation analysis may not yield results simply because the relationship is nonlinear (expressed, for example, as a parabola).
3. The mere fact of correlation does not provide grounds for asserting which of the variables precedes or causes changes, or that the variables are generally causally related to each other, for example, due to the action of a third factor.

Application area

This method of processing statistical data is very popular in economics and social sciences (in particular in psychology and sociology), although the scope of application of correlation coefficients is extensive: quality control of industrial products, metallurgy, agrochemistry, hydrobiology, biometrics and others.

The popularity of the method is due to two factors: correlation coefficients are relatively easy to calculate, and their use does not require special mathematical training. Combined with its ease of interpretation, the ease of application of the coefficient has led to its widespread use in the field of statistical data analysis.

False correlation

Often, the tempting simplicity of correlation research encourages the researcher to make false intuitive conclusions about the presence of a cause-and-effect relationship between pairs of characteristics, while correlation coefficients establish only statistical relationships.

Modern quantitative social science methodology has, in fact, abandoned attempts to establish cause-and-effect relationships between observed variables using empirical methods. Therefore, when researchers in the social sciences talk about establishing relationships between the variables being studied, either a general theoretical assumption or a statistical dependence is implied.

see also

• Autocorrelation function
• Cross-correlation function
• Covariance
• Determination coefficient
• Regression analysis

Wikimedia Foundation. 2010.